"빗면"의 두 판 사이의 차이
(새 문서: 썸네일|300픽셀|'''빗면'''( slope inclined plane) '''빗면'''( slope inclined plane)은 가장 원시적인 도구의 하나로, 높이가 다른 지...) |
|||
| 1번째 줄: | 1번째 줄: | ||
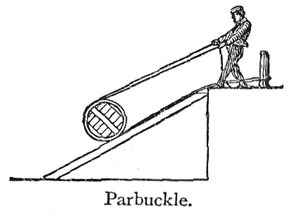
[[파일:빗면.png|썸네일|300픽셀|'''빗면'''( slope inclined plane)]] | [[파일:빗면.png|썸네일|300픽셀|'''빗면'''( slope inclined plane)]] | ||
| − | '''빗면'''( slope inclined plane)은 가장 원시적인 [[도구]]의 하나로, 높이가 다른 지점을 잇는 평평한 면을 이른다. 어떤 무거운 물체를 들 때 수직으로 드는 것보다 빗면을 이용해서 미는 것이 훨씬 쉽다. 그 이유는 더 긴 거리를 가기 때문에 하는 일은 같지만, 더 적은 힘을 이용해서 들어올릴 수 있기 때문이다. | + | '''빗면'''(slope inclined plane)은 가장 원시적인 [[도구]]의 하나로, 높이가 다른 지점을 잇는 평평한 면을 이른다. 어떤 무거운 물체를 들 때 수직으로 드는 것보다 빗면을 이용해서 미는 것이 훨씬 쉽다. 그 이유는 더 긴 거리를 가기 때문에 하는 일은 같지만, 더 적은 힘을 이용해서 들어올릴 수 있기 때문이다. |
W=F↓×s↑ 힘의 이득, 이동거리 손해 | W=F↓×s↑ 힘의 이득, 이동거리 손해 | ||
2024년 8월 27일 (화) 11:36 판
빗면(slope inclined plane)은 가장 원시적인 도구의 하나로, 높이가 다른 지점을 잇는 평평한 면을 이른다. 어떤 무거운 물체를 들 때 수직으로 드는 것보다 빗면을 이용해서 미는 것이 훨씬 쉽다. 그 이유는 더 긴 거리를 가기 때문에 하는 일은 같지만, 더 적은 힘을 이용해서 들어올릴 수 있기 때문이다.
W=F↓×s↑ 힘의 이득, 이동거리 손해
개요
수평면에 대하여 일정한 각도로 기운 평면으로 사면(斜面)이라고도 한다.
수평면과 빗면이 이루는 각을 경사각이라 한다. 빗면을 사용하면 적은 힘으로 물체를 움직일 수 있다. 무게가 10N인 물체를 수직으로 들어 올리려면 10N의 힘이 든다. 하지만 빗면을 이용하여 끌어올리면 그보다 작은 힘을 사용해 위쪽으로 물체를 이동시킬 수 있다. 무거운 짐이 실린 수레의 경우 수직으로 들어서 계단을 오르는 것은 불가능하지만 경사로를 이용해 밀면 쉽게 높은 곳에 갈 수 있다. 이것은 빗면이 물체를 위쪽으로 미는 수직항력과 중력의 일정 성분이 평형을 이루기 때문이다. 마찰을 무시하고 빗면의 경사각을 θ라 하면, 질량이 m kg인 물체를 끌어올리는 데 필요한 힘은 F = m·g·sinθ (g는 중력가속도)이다. 따라서 경사각이 작을수록 더 적은 힘으로 물체를 움직일 수 있다. 그러나 높이 h만큼 움직이기 위해서 필요한 빗면의 거리는 h/sinθ가 되어 물체에 한 일의 양은 수직으로 들어 올릴 경우와 같다.
W=F·∆s=mgh
W'=F'·∆s'=m·g·sinθ×h/sinθ
∴W=W'
빗면의 원리를 응용한 것으로 쐐기와 나사가 있다. 틈을 벌리거나 물체를 쪼갤 때 양쪽으로 바로 잡아당기는 것보다 쐐기의 빗면을 이용하여 벌리는 것이 더 적은 힘이 든다. 원기둥에 감겨 있는 나사선을 평면으로 펼치면 빗면이 된다. 못을 직접 수직으로 넣는 것보다 나사선을 타고 밀어 넣는 것이 더 적은 힘이 든다. 쐐기나 나사도 힘에는 이득을 보지만 한 일은 사용하지 않은 경우와 같다.
빗면의 원리
빗면의 경사가 완만할수록 물체를 끌어올리는 힘의 크기는 작아지고, 물체를 이동시켜야하는 거리는 길어진다는 것이 빗면의 원리이다.
빗면을 사용하여 같은 높이까지 물체를 끌어올릴 때 빗면의 경사가 완만할수록 물체를 끌어올리는데 필요한 힘의 크기는 작아진다. 즉 빗면을 사용하면 물체의 무게보다 작은 힘으로 물체를 들어올릴 수 있다.
꼬불꼬불한 산길을 넘어갈 때 산의 경가면을 따라 만들어진 비탈길을 이용해 넘어간다. 빗면은 기계가 없던 고대부터 이용되어 왔다. 고인돌의 덮개돌을 얹을 때나 이집트에서 피라미드를 만들 때도 빗면을 이용하여 무거운 돌을 높이 올렸을 거라 추측하고 있다.
꼬불고불한 산길처럼 계단, 나사못, 병따개, 도끼날, 쐐기, 사다리차, 지퍼 등이 빗면의 원리를 이용는 예이다.
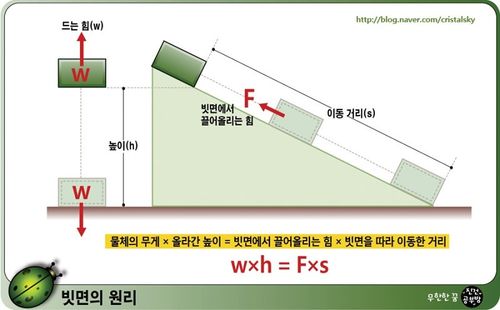
- 빗면에서 끌어올리는 힘 (F)× 빗면을 따라 이동한 거리(s) = 물체의 무게(w) × 올라간 높이(h)
예제) 무게가 20N 인 물체를 길이가 5m인 빗면을 사용하여 끝까지 끌어 올렸더니 물체가 2m 올라갔다. 이 물체를 끌어 올릴 때 작용한 힘의 크기는 얼마일까?
빗면에서 끌어올리는 힘(F) × 이동거리 5m=물체의 무게 20N × 올라간 높이 2m
F×5=40, F= 40÷5=8 답 : 8N
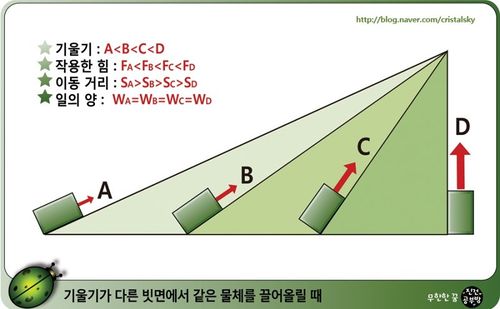
- 기울기가 다른 빗면에서의 물체를 끌어올릴 때의 일
- 빗면의 기울기 : A < B < C <D
- 필요한 힘 : A < B < C <D
- 이동거리 : D < C < B < A
- 한 일의 양 A = B = C
경사가 완만할수록 물체를 이동시키는 데 필요한 힘의 크기는 작아지지만 물체를 이동시켜야하는 거리는 길어지기 때문에 빗면을 사용하면 빗면을 사용하지 않을 때와 한 일의 양은 같다. 하지만 빗면을 이용하면, 작은 힘으로 물체를 들어올릴 수 있다.
일의 원리
지레, 움직 도르래, 빗면 등의 도구를 사용하면 작은 힘으로 물체를 움직일 수 있다. 하지만 힘이 줄어든 만큼 이동 거리가 늘어나게 된다. 이처럼 도구를 사용할 때와 도구를 사용하지 않을 때 한 일의 양은 같다. 이를 일의 원리라 한다.
그렇다면 왜 도구를 사용하여 일을 하는 것일까? 고정 도르래를 사용하면 힘의 방향을 바꿀 수 있고, 지레, 움직 도르래, 빗면 등의 도구를 이용하면 작은 힘으로 물체를 움직일 수 있다. 즉, 도구를 사용하면 힘의 이득을 얻거나, 힘의 방향을 바꾸어 일을 할 수 있다.
참고자료
- 〈빗면〉, 《위키백과》
- 〈빗면〉, 《두산백과》
- 에스웰 공부방, 〈중2 과학 6단원 도구와 일의 원리- 빗면〉, 《네이버 블로그》, 2016-10-16
같이 보기
{{기계|검토 필요]]

 위키원
위키원