"동형암호"의 두 판 사이의 차이
(→특징) |
잔글 (→참고 자료) |
||
| (사용자 3명의 중간 판 16개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''동형암호'''(Homomorphic Encryption;HE)는 [[암호화]]된 데이터를 복호화 없이도 연산할 수 있는 암호 기술이다. [[암호화]]된 상태에서 연산한 | + | '''동형암호'''(Homomorphic Encryption;HE)는 <!--동형 암호,완전동형암호,동형암호화,동형 암호화,동형 암호 기술,Homomorphic Encryption, HE-->[[암호화]]된 데이터를 복호화 없이도 연산할 수 있는 암호 기술이다. [[암호화]]된 상태에서 연산한 결괏값을 복호화하면 평문 상태의 데이터를 연산한 결과와 동일한 값을 얻을 수 있게 된다. 이렇게 [[암호화]]한 상태에서나 하지 않은 상태에서 분석한 결과물의 형태가 같다는 의미에서 동형이라고 한다.<ref name="개인정보보호">개인정보보호, 〈[https://blog.naver.com/n_privacy/221460985974 안전한 개인정보 활용을 위한 동형 암호]〉, 《네이버 블로그》, 2019-02-08</ref> |
== 개요 == | == 개요 == | ||
| − | 동형암호는 정보를 [[암호화]]한 상태에서 각종 연산을 했을 때, 그 결과가 [[암호화]]하지 않은 상태의 연산 결과와 동일하게 나오는 4세대 암호체계를 말한다. 동형암호는 [[ | + | 동형암호는 정보를 [[암호화]]한 상태에서 각종 연산을 했을 때, 그 결과가 [[암호화]]하지 않은 상태의 연산 결과와 동일하게 나오는 4세대 암호체계를 말한다. 동형암호는 [[튜링 완전성]]을 갖는다. 이로부터 통계처리뿐만 아니라 검색, 기계학습까지 가능하다. 동형암호는 데이터를 사용하는 환경에 키가 저장되지 않는다. 키를 함께 제공하지 않고 [[암호화]]한 상태의 데이터만 맡겨 계산을 할 수 있게 해줌으로써 보안을 높여 해커의 데이터 유출을 막을 수 있다. [[암호화]]한 상태에서나 하지 않은 상태에서 분석한 결과물의 형태가 같다는 의미에서 '동형(同型)'이라는 이름이 붙었다.<ref name="과학기술정보통신부">과학기술정보통신부, 〈[https://blog.naver.com/with_msip/221517757125 4세대 암호, '동형암호'를 소개합니다!]〉, 《네이버 블로그》, 2019-04-19</ref><ref>IMDARC, 〈[http://imdarc.math.snu.ac.kr/board_apmJ27/3058 암호기술 혁명 - 동형암호]〉, 《IMDARC》, 2018-10-26</ref> |
== 등장 배경 == | == 등장 배경 == | ||
| − | [[암호화]]는 데이터의 보안에 필수이지만, 기존의 [[암호화]] 기술은 [[암호화]]된 상태에서 연산, 탐색, 분석 등의 작업이 불가능했다. 기존의 [[암호화]]는 평문을 복호화키가 없이는 난수와 구별할 수 없는 문자열로 변환하는 것을 목표로 하므로 암호문을 가지고 | + | [[암호화]]는 데이터의 보안에 필수이지만, 기존의 [[암호화]] 기술은 [[암호화]]된 상태에서 연산, 탐색, 분석 등의 작업이 불가능했다. 기존의 [[암호화]]는 평문을 복호화키가 없이는 난수와 구별할 수 없는 문자열로 변환하는 것을 목표로 하므로 암호문을 가지고 의미 있는 작업을 수행하는 것은 불가능하였다. 이와 달리 Rivest, Addleman and Dertouzous (1978)에 의해 제안된 동형암호는 [[암호화]]된 상태에서도 복호화키 없이 평문의 연산을 수행할 수 있어서 이상적인 암호로 여겨졌으나, 그 안전성에 대해서는 Gentry가 처음으로 안전한 동형암호를 제시한 2009년 전까지 30여 년간 미해결 문제였다. Gentry (2009)는 그의 논문에서 정수론과 격자분야의 난제에 기반을 둔 동형암호를 설계하였고 그 안전성이 난제로 환원됨을 증명하였는데, 처음에는 매우 비효율적이었다. 그러나 그 후 많은 연구자의 개선을 거치면서 동형암호기술은 최근 들어 실용화를 앞두고 있으며 2011년 MIT Technical Review에서 10대 Emerging Technology로도 선정이 되는 등 IT 전반에 큰 이슈가 되고 있다.<ref name ="pdf">천정희, 어윤희, 김재윤, 〈[http://fisk.or.kr/board_common/file_download.asp?Board_Key=53&File_Key=75&flag=5 개인정보가 보호되는 동형암호기반 금융데이터분석]〉, 《한국금융정보학회》, 2019-02-28</ref> |
== 특징 == | == 특징 == | ||
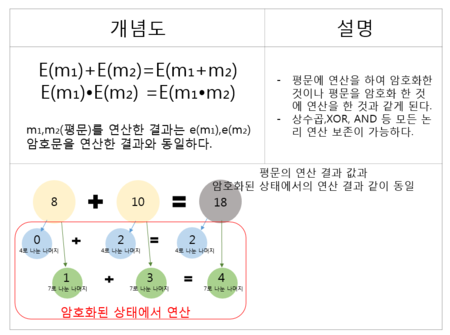
[[파일:동형암호.PNG |썸네일|450픽셀|'''동형암호'''의 개념도 및 예시]] | [[파일:동형암호.PNG |썸네일|450픽셀|'''동형암호'''의 개념도 및 예시]] | ||
| − | 평문 <math>m_1</math>, <math>m_2</math>에 대한 암호문 <math>c_1</math>, <math>c_2</math>가 주어졌을 때 <math>m_1+m_2</math>의 암호문을 만드는 문제를 생각할 때, 이 암호에 대한 비밀키를 가지고 있으면 암호문 <math>c_1</math>, <math>c_2</math>를 복호화하여 평문 <math>m_1</math>, <math>m_2</math>를 얻고 이를 더한 후 다시 [[암호화]]하여 <math>m_1+m_2</math>의 암호문을 계산할 수 있다. 동형암호에서는 이 과정을 비밀키 없이 수행할 수 있으며, 덧셈뿐 아니라 곱셈도 수행할 수 있고 더 나아가 컴퓨터가 하는 모든 연산을 복호화 없이 수행할 수 있다. 실제 컴퓨터가 하는 모든 연산은 and, or, not 등의 | + | 평문 <math>m_1</math>, <math>m_2</math>에 대한 암호문 <math>c_1</math>, <math>c_2</math>가 주어졌을 때 <math>m_1+m_2</math>의 암호문을 만드는 문제를 생각할 때, 이 암호에 대한 비밀키를 가지고 있으면 암호문 <math>c_1</math>, <math>c_2</math>를 복호화하여 평문 <math>m_1</math>, <math>m_2</math>를 얻고 이를 더한 후 다시 [[암호화]]하여 <math>m_1+m_2</math>의 암호문을 계산할 수 있다. 동형암호에서는 이 과정을 비밀키 없이 수행할 수 있으며, 덧셈뿐 아니라 곱셈도 수행할 수 있고 더 나아가 컴퓨터가 하는 모든 연산을 복호화 없이 수행할 수 있다. 실제 컴퓨터가 하는 모든 연산은 and, or, not 등의 논리연산 합성으로 이루어져 있음으로 이들 세 가지 논리연산만 [[암호화]]한 상태에서 수행할 수 있으면 이를 반복하여 임의의 연산을 [[암호화]]한 상태에서 수행할 수 있다. 이에 반해 [[암호화]]한 상태에서 일부 연산만 수행할 수 있는 암호를 [[부분동형암호]](partial homomorphic encryption)이라고 하는데 유한체 위의 ElGamal암호가 곱셈만 가능한 [[곱셈동형암호]](multiplicative homomorphic encryption)이고 Okamoto-Uchiyama암호, Pailler암호가 대표적으로 덧셈만 보호하는 [[덧셈동형암호]](additive homomorphic encryption)이다. 다만 Gentry가 제안한 동형암호는 제한된 횟수의 연산만을 수행할 수 있었는데, 이는 어느 정도의 연산을 수행하고 나면 암호문 안에 들어 있는 잡음(noise)이 커져서 평문이 훼손되기 때문이다. 만일 이 잡음이 큰 암호문을 평문을 유지하면서 잡음이 작은 새로운 암호문으로 바꿀 수 있으면 다시 연산을 지속할 수 있게 되는데 이러한 과정을 재부팅(bootstrapping)이라 한다. (물론 복호화키 없이 수행하여야 한다.) 이 재부팅 과정이 허용되는 암호는 무한한 횟수의 연산도 가능하게 되며 이렇게 임의의 연산을 무한히 계속 할 수 있는 암호를 [[완전동형암호]](fully homomorphic encryption)라고 부른다. 이에 반해 제한된 횟수의 연산만 수행할 수 있는 암호는 [[제한동형암호]](somewhat homomorphic encryption)라 부른다. [[완전동형암호]]는 [[암호화]]된 상태의 데이터에 대해서도 컴퓨터로 할 수 있는 모든 연산을 원하는 대로 수행할 수 있으므로 검색이나 통계적인 분석뿐 아니라 기계학습이나 영상처리 등 매우 복잡한 연산에도 적용할 수 있다. 개인정보를 기반으로 한 기계학습의 경우 [[암호화]]된 데이터상에서 분석을 수행하고 분석결과를 확인하는 마지막 단계에서만 복호화하여 개인정보 열람을 최소화할 수 있다. [[완전동형암호]]는 컴퓨터가 하는 모든 연산을 [[암호화]]한 상태로도 수행할 수 있는 이론적 강점이 있지만 평문 연산보다 암호문 연산의 효율성에서는 떨어진다는 단점이 있다. 그러나 응용 연산의 종류에 따라 속도의 차이가 크기 때문에 개별 연산에 대해 최적화하여 적용하는 방법으로 효율성을 높일 수 있다. 또한 동형암호 연구가 아직 초기 단계이므로 알고리즘의 개발에 따라 효율이 크게 향상될 여지가 있다. 예를 들면, 동형암호 연산 중에 가장 비효율적인 재부팅 시간이 2011년도에는 30분이었던 것이 2013년에는 0.32초, 2015년에는 0.02초까지 계산속도가 빠르게 개선되고 있다.<ref name ="pdf"></ref> |
* '''구현 원리''' | * '''구현 원리''' | ||
| 16번째 줄: | 16번째 줄: | ||
|- | |- | ||
| 부분 동형 암호<br>(SHE) || style="text-align:left; padding: 11px" | | | 부분 동형 암호<br>(SHE) || style="text-align:left; padding: 11px" | | ||
| − | * Somewhat homomorphic encryption(SHE), 덧셈과 곱셈 모두 지원(곱셈은 특정 횟수 | + | * Somewhat homomorphic encryption(SHE), 덧셈과 곱셈 모두 지원(곱셈은 특정 횟수 K 번까지만 지원하도록 설계) |
* ElGamal암호가 곱셈만 가능한 곱셈 동형 암호 | * ElGamal암호가 곱셈만 가능한 곱셈 동형 암호 | ||
|- | |- | ||
| 스쿼싱<br>(Squashing) || style="text-align:left; padding: 11px" | | | 스쿼싱<br>(Squashing) || style="text-align:left; padding: 11px" | | ||
* 복호화 알고리즘 및 공개키 일부 변형 | * 복호화 알고리즘 및 공개키 일부 변형 | ||
| − | * 곱셈 | + | * 곱셈 k 회 이하만 적용 시 복호화 가능(복호화 알고리즘이 동형으로 계산 가능) |
* 노이즈 증가 감소, 평문 변형되지 않도록 구성하는 원리 | * 노이즈 증가 감소, 평문 변형되지 않도록 구성하는 원리 | ||
|- | |- | ||
| 43번째 줄: | 43번째 줄: | ||
|}<ref name="구현원리"></ref> | |}<ref name="구현원리"></ref> | ||
| − | * ''' | + | * '''격자 기반암호''' |
| − | : 동형암호는 암호체계 중 높은 난이도를 가졌다고 언급되는 | + | : 동형암호는 암호체계 중 높은 난이도를 가졌다고 언급되는 격자 기반암호(lattice problem)의 한 종류이다. 3차원까지는 인간의 머릿속에서 이미지를 그릴 수 있지만 4차원부터는 오직 수식으로만 표현이 가능하다. 수백 차원의 격자 위의 임의 위치에서 가장 가까운 점을 찾기가 어렵다는 것을 근거로 하여 동형암호는 계산되는 데 엄청난 시간이 필요하고 양자 컴퓨터도 찾아내기 힘들다. 그로 인해 동형암호는 양자컴퓨팅의 보안 방법 중 하나로 주목받고 있다.<ref name="과학기술정보통신부"></ref> |
| − | * ''' | + | * '''성능 비교''' |
| − | + | : 공개키 암호와 동형암호의 성능 비교 | |
| − | |||
| − | |||
| − | : 공개키 암호와 동형암호의 | ||
: {| class="wikitable" width=600 style="color:balck; text-align: center; background-color:#F8F9FA;" | : {| class="wikitable" width=600 style="color:balck; text-align: center; background-color:#F8F9FA;" | ||
! || 공개키<br>크기 || 암호문<br>크기 || 평문<br>크기 || 암호화<br>시간 || 복호화<br>시간 || 덧셈<br>시간 || 곱셈<br>시간 || 허용<br>depth || 안전성 | ! || 공개키<br>크기 || 암호문<br>크기 || 평문<br>크기 || 암호화<br>시간 || 복호화<br>시간 || 덧셈<br>시간 || 곱셈<br>시간 || 허용<br>depth || 안전성 | ||
| 72번째 줄: | 69번째 줄: | ||
== 종류 == | == 종류 == | ||
| − | [[파일: | + | [[파일:천정희.jpg|썸네일|200픽셀|'''[[천정희]]''']] |
| + | |||
* '''혜안(HeaAn)''' | * '''혜안(HeaAn)''' | ||
| − | : [[혜안]](HeaAn) 알고리즘은 [[천정희]] 교수가 설립한 '크립토 랩'에서 동형암호학 알고리즘을 획기적으로 | + | : [[혜안]](HeaAn) 알고리즘은 [[천정희]] 교수가 설립한 '크립토 랩'에서 동형암호학 알고리즘을 획기적으로 개선한 알고리즘이다. 전산의 이론을 보면 비트 단위의 더하기와 곱하기를 실행할 수 있을 때, 실제로 컴퓨터가 하는 모든 연산을 수행할 수 있다는 증명할 수 있다. 이를 튜링 완전성이라고도 한다. 동형암호가 모든 것을 할 수 있다는 건 증명이 됐으나, 그것을 실용적으로 쓸 수 있는지 확인을 하기 위해서 데이터들을 더하는 32비트 데이터 여러 개를 덧셈과 곱셈 연산을 해보았을 때, 결과는 가능하지만, 속도가 너무 느리다는 결론이 나온다. 데이터를 곱하면 곱할수록 숫자가 다룰 수 없을 만큼 큰 크기가 돼버리기 때문이다. 숫자를 반올림하여 유효숫자가 아닌 숫자를 버리고 짧은 숫자들만 연산을 진행하는 것을 [[근사계산]]이라고 하는데 [[근사계산]]을 수행할 때, 연산마다 라운딩을 할 수 있도록 하여 다른 암호보다 월등히 좋은 성능을 보이게 된 것이다.<ref>HASHED, 〈[https://medium.com/hashed-kr/homomorphicencryption-blockchain-d783becbaabb 해시드 인터뷰: 서울대학교 천정희 교수 (Jung-hee Cheon), 동형암호와 블록체인]〉, 《Medium》, 2019-05-22</ref> |
* '''HELib''' | * '''HELib''' | ||
| − | : HElib는 | + | : HElib는 동형암호(HE)를 구현하는 소프트웨어 라이브러리이다. 현재 Smart-Vercauteren 암호문 패킹 기술과 Gentry-Halevi-Smart 최적화의 효과적인 사용에 주로 초점을 맞추어 동질성 평가를 빠르게 수행하는 많은 최적화와 함께 Brakerski-Gentry-Vaikuntanathan (BGV) 체계의 구현이 가능하다. 기본 암호 시스템은 동형에 적용 할 수 있는 일련의 운용을 정의하고 비용을 명시한다는 점에서 HElib의 '하드웨어 플랫폼'과 동일한 역할을 한다. 이 플랫폼은 SIMD 환경(Intel SSE 등과 유사)이지만 고유한 비용 지표와 매개변수를 가지고 있다. 동형 암호화를 위해 공개키가 구성되는 방식은 키 스위칭 매트릭스 때문에 비용이 많이 든다. 각 매트릭스는 공개키에 수 메가바이트를 추가하며, HElib에서는 공개키에 수백 개의 매트릭스가 있을 수 있다. 연구원들은 일반적인 작업에 대해 매트릭스의 크기를 33~50% 줄일 수 있다고 말한다. 또한, HElib는 연구 수준 프로젝트이며 유사 암호화를 위한 어셈블리 언어를 사용한다.<ref>Richard Chirgwin, 〈[https://www.theregister.co.uk/2018/03/08/ibm_faster_homomorphic_encryption/ IBM's homomorphic encryption accelerated to run 75 times faster]〉, 《The Register》, 2018-03-08</ref><ref>GitHub 공식 홈페이지 - 〈[https://github.com/homenc/HElib HElib]〉</ref> |
| + | |||
| + | * '''SEAL | ||
| + | : 마이크로소프트에서 만든 동형암호 라이브러리이다. <ref>GitHub 공식 홈페이지 - 〈[https://github.com/microsoft/SEAL SEAL]〉</ref> | ||
| − | * | + | == 장단점 == |
| − | : | + | * 장점 |
| + | : 동형암호는 암호문을 복호화하지 않아도 검색, 통계 처리 및 기계 학습이 가능하고, 데이터를 처리하는 중간 과정에서 복호화하지 않아도 되므로, 데이터 유출 위험이 감소하는 장점이 있다. | ||
| + | |||
| + | * 단점 | ||
| + | : 단점은 기존 암호의 확장률(평문 대비 암호문이 커지는 비율)에 비해 10배에서 100배 정도 커질 수 있고, 암복호화 속도가 1ms인 RSA 대비 수십 ms가 소요되며, 암호문 곱셈 연산의 경우, 수백ms가 소요된다. 한편 앞에서 언급했던 노이즈 감소를 위한 재부팅 시간이 필수적으로 필요하며, 2015년 기준 재부팅 시간이 0.02초 정도로 보고되었다.<ref name="LG">LG CNS, 〈[https://blog.lgcns.com/2045 4세대 암호, 완전동형암호란?]〉, 《LG CNS 블로그》, 2019-07-16</ref> | ||
== 전망 == | == 전망 == | ||
| − | 동형암호는 의료 분야, | + | 동형암호는 의료 분야, 금융 분야 뿐만 아니라 [[블록체인]]과 양자컴퓨팅 분야에 활용할 수 있을 것으로 예상된다. 블록체인은 연산 과정을 모두 파악할 수 있는 특성이 있어 민감한 개인정보를 다루기 어려웠는데 동형 암호 기술을 활용한다면 효용성이 매우 상승할 것으로 기대된다. 또한 클라우드 기반 데이터 분석을 가능하게 하여 데이터를 활용하는 분야에 유용한 정보를 제공할 수 있을 것으로 전망된다.<ref name="과학기술정보통신부"></ref> |
| + | |||
| + | == 예시 == | ||
| + | * [[클라우드]] | ||
| + | : 삼성 SDS는 2019년 3월 14일 최근 기업들이 핵심업무까지 [[클라우드]]로 전환하면서 보안에 큰 관심을 기울이고 있어서 인공지능(AI) 기술을 접목한 보안관제서비스로 운영되는 [[클라우드]] 환경의 보안 공백을 '제로화' 하고, 정보의 흐름이나 보안 설정 등에 문제가 생기면 스스로 찾아서 차단해주는 정보 유출방지 서비스를 제공한다고 했다. 또한, [[암호화]]된 데이터를 복호화하지 않고 그대로 분석해 결과까지 암호화된 상태로 제공하는 '동형암호' 기술을 연내 상용화할 계획이라고 했다. 덧붙여, 서울대학교 [[천정희]] 교수팀과 협력해 동형암호의 최대 난관인 분석속도 문제를 해소한 원천기술을 확보했고 이미 시범적으로 금융, 의료 등 민감한 데이터를 동형암호로 분석하는 데 성공해 현재도 실제 적용이 가능한 수준이라고 설명했다.<ref>남도영, 〈[https://www.msn.com/ko-kr/news/techandscience/%EC%82%BC%EC%84%B1sds-%EB%B9%84%EB%B0%80%EB%B3%91%EA%B8%B0-%EB%8F%99%ED%98%95%EC%95%94%ED%98%B8%EB%A1%9C-%ED%81%B4%EB%9D%BC%EC%9A%B0%EB%93%9C-%EB%B3%B4%EC%95%88-%EC%9E%90%EC%8B%A0%EA%B0%90/ar-BBUKpcj 삼성SDS, 비밀병기 '동형암호'로 클라우드 보안 '자신감']〉, 《msn 뉴스》, 2019-03-14</ref> | ||
| + | |||
| + | * 생체인식 | ||
| + | : 출입 통제에 사용하는 생체 정보를 안전하게 처리할 수 있다. 완전 동형암호화된 지문 등의 생체 정보를 복호화하지 않고, 암호화된 채로 인증을 수행할 수 있다면, 생체 정보를 복호화해 평문으로 보관하거나, 검증을 위해 원본을 전송할 필요 없이 받은 암호문과 보관 중인 암호화된 생체 정보를 비교해 일치 여부를 확인할 수 있도록 할 수 있다. 2018년 11월 '개인식별 방지 기술 세미나'에서 한국스마트인증(대표 문기봉)이 이러한 완전 동형암호기술을 활용해 홍채 인증 기술을 개량 발전 시켜 인증 시간을 0.25초로 앞당긴 시스템을 발표했다. | ||
| + | |||
| + | * 금융 | ||
| + | : 완전 동형암호는 컴퓨터가 할 수 있는 연산을 모두 수행할 수 있어 데이터의 기밀성을 보호하면서 금융 데이터를 동형 기계 학습의 훈련 단계에서 활용할 수 있다. 동형 기계 학습의 훈련 단계에서 암호화된 데이터 연산을 통해 예측•분류 모형을 얻고 그 모형으로부터 실시간 계산이 필요한 예측 단계에서는 함수 암호를 사용한다. 동형 기계 학습은 데이터의 기밀성을 보호할 수 있어 개인의 민감한 정보의 유출에 대한 보안 문제를 해결할 수 있으며 데이터의 손실 없이 신용도 평가 예측 모형의 고도화가 가능하다고 할 수 있다. 실제 사례로, 2018년 11월 ‘개인식별 방지 기술 세미나’에서 코리아크레딧뷰로(KCB, 대표 강문호)는 50만 명의 신용 데이터를 동형암호화된 상태에서 기계 학습을 수행해 개인정보를 보호하면서 신용 평가 모형의 신뢰성, 정확성, 안전성을 성공적으로 확보할 수 있음을 검증했다.<ref name="LG"></ref> | ||
{{각주}} | {{각주}} | ||
| − | == | + | == 참고자료 == |
* 개인정보보호, 〈[https://blog.naver.com/n_privacy/221460985974 안전한 개인정보 활용을 위한 동형 암호]〉, 《네이버 블로그》, 2019-02-08 | * 개인정보보호, 〈[https://blog.naver.com/n_privacy/221460985974 안전한 개인정보 활용을 위한 동형 암호]〉, 《네이버 블로그》, 2019-02-08 | ||
* 과학기술정보통신부, 〈[https://blog.naver.com/with_msip/221517757125 4세대 암호, '동형암호'를 소개합니다!]〉, 《네이버 블로그》, 2019-04-19 | * 과학기술정보통신부, 〈[https://blog.naver.com/with_msip/221517757125 4세대 암호, '동형암호'를 소개합니다!]〉, 《네이버 블로그》, 2019-04-19 | ||
| 96번째 줄: | 111번째 줄: | ||
* Richard Chirgwin, 〈[https://www.theregister.co.uk/2018/03/08/ibm_faster_homomorphic_encryption/ IBM's homomorphic encryption accelerated to run 75 times faster]〉, 《The Register》, 2018-03-08 | * Richard Chirgwin, 〈[https://www.theregister.co.uk/2018/03/08/ibm_faster_homomorphic_encryption/ IBM's homomorphic encryption accelerated to run 75 times faster]〉, 《The Register》, 2018-03-08 | ||
* GitHub 공식 홈페이지 - 〈[https://github.com/homenc/HElib HElib]〉 | * GitHub 공식 홈페이지 - 〈[https://github.com/homenc/HElib HElib]〉 | ||
| − | * GitHub 공식 홈페이지 - 〈[https://github.com/ | + | * GitHub 공식 홈페이지 - 〈[https://github.com/microsoft/SEAL SEAL]〉 |
| + | * 남도영, 〈[https://www.msn.com/ko-kr/news/techandscience/%EC%82%BC%EC%84%B1sds-%EB%B9%84%EB%B0%80%EB%B3%91%EA%B8%B0-%EB%8F%99%ED%98%95%EC%95%94%ED%98%B8%EB%A1%9C-%ED%81%B4%EB%9D%BC%EC%9A%B0%EB%93%9C-%EB%B3%B4%EC%95%88-%EC%9E%90%EC%8B%A0%EA%B0%90/ar-BBUKpcj 삼성SDS, 비밀병기 '동형암호'로 클라우드 보안 '자신감']〉, 《msn 뉴스》, 2019-03-14 | ||
| + | * LG CNS, 〈[https://blog.lgcns.com/2045 4세대 암호, 완전동형암호란?]〉, 《LG CNS 블로그》, 2019-07-16 | ||
== 같이 보기 == | == 같이 보기 == | ||
| 105번째 줄: | 122번째 줄: | ||
* [[암호화]] | * [[암호화]] | ||
* [[천정희]] | * [[천정희]] | ||
| + | * [[클라우드]] | ||
{{암호 알고리즘|검토 필요}} | {{암호 알고리즘|검토 필요}} | ||
2021년 5월 8일 (토) 00:17 기준 최신판
동형암호(Homomorphic Encryption;HE)는 암호화된 데이터를 복호화 없이도 연산할 수 있는 암호 기술이다. 암호화된 상태에서 연산한 결괏값을 복호화하면 평문 상태의 데이터를 연산한 결과와 동일한 값을 얻을 수 있게 된다. 이렇게 암호화한 상태에서나 하지 않은 상태에서 분석한 결과물의 형태가 같다는 의미에서 동형이라고 한다.[1]
개요[편집]
동형암호는 정보를 암호화한 상태에서 각종 연산을 했을 때, 그 결과가 암호화하지 않은 상태의 연산 결과와 동일하게 나오는 4세대 암호체계를 말한다. 동형암호는 튜링 완전성을 갖는다. 이로부터 통계처리뿐만 아니라 검색, 기계학습까지 가능하다. 동형암호는 데이터를 사용하는 환경에 키가 저장되지 않는다. 키를 함께 제공하지 않고 암호화한 상태의 데이터만 맡겨 계산을 할 수 있게 해줌으로써 보안을 높여 해커의 데이터 유출을 막을 수 있다. 암호화한 상태에서나 하지 않은 상태에서 분석한 결과물의 형태가 같다는 의미에서 '동형(同型)'이라는 이름이 붙었다.[2][3]
등장 배경[편집]
암호화는 데이터의 보안에 필수이지만, 기존의 암호화 기술은 암호화된 상태에서 연산, 탐색, 분석 등의 작업이 불가능했다. 기존의 암호화는 평문을 복호화키가 없이는 난수와 구별할 수 없는 문자열로 변환하는 것을 목표로 하므로 암호문을 가지고 의미 있는 작업을 수행하는 것은 불가능하였다. 이와 달리 Rivest, Addleman and Dertouzous (1978)에 의해 제안된 동형암호는 암호화된 상태에서도 복호화키 없이 평문의 연산을 수행할 수 있어서 이상적인 암호로 여겨졌으나, 그 안전성에 대해서는 Gentry가 처음으로 안전한 동형암호를 제시한 2009년 전까지 30여 년간 미해결 문제였다. Gentry (2009)는 그의 논문에서 정수론과 격자분야의 난제에 기반을 둔 동형암호를 설계하였고 그 안전성이 난제로 환원됨을 증명하였는데, 처음에는 매우 비효율적이었다. 그러나 그 후 많은 연구자의 개선을 거치면서 동형암호기술은 최근 들어 실용화를 앞두고 있으며 2011년 MIT Technical Review에서 10대 Emerging Technology로도 선정이 되는 등 IT 전반에 큰 이슈가 되고 있다.[4]
특징[편집]
평문 , 에 대한 암호문 , 가 주어졌을 때 의 암호문을 만드는 문제를 생각할 때, 이 암호에 대한 비밀키를 가지고 있으면 암호문 , 를 복호화하여 평문 , 를 얻고 이를 더한 후 다시 암호화하여 의 암호문을 계산할 수 있다. 동형암호에서는 이 과정을 비밀키 없이 수행할 수 있으며, 덧셈뿐 아니라 곱셈도 수행할 수 있고 더 나아가 컴퓨터가 하는 모든 연산을 복호화 없이 수행할 수 있다. 실제 컴퓨터가 하는 모든 연산은 and, or, not 등의 논리연산 합성으로 이루어져 있음으로 이들 세 가지 논리연산만 암호화한 상태에서 수행할 수 있으면 이를 반복하여 임의의 연산을 암호화한 상태에서 수행할 수 있다. 이에 반해 암호화한 상태에서 일부 연산만 수행할 수 있는 암호를 부분동형암호(partial homomorphic encryption)이라고 하는데 유한체 위의 ElGamal암호가 곱셈만 가능한 곱셈동형암호(multiplicative homomorphic encryption)이고 Okamoto-Uchiyama암호, Pailler암호가 대표적으로 덧셈만 보호하는 덧셈동형암호(additive homomorphic encryption)이다. 다만 Gentry가 제안한 동형암호는 제한된 횟수의 연산만을 수행할 수 있었는데, 이는 어느 정도의 연산을 수행하고 나면 암호문 안에 들어 있는 잡음(noise)이 커져서 평문이 훼손되기 때문이다. 만일 이 잡음이 큰 암호문을 평문을 유지하면서 잡음이 작은 새로운 암호문으로 바꿀 수 있으면 다시 연산을 지속할 수 있게 되는데 이러한 과정을 재부팅(bootstrapping)이라 한다. (물론 복호화키 없이 수행하여야 한다.) 이 재부팅 과정이 허용되는 암호는 무한한 횟수의 연산도 가능하게 되며 이렇게 임의의 연산을 무한히 계속 할 수 있는 암호를 완전동형암호(fully homomorphic encryption)라고 부른다. 이에 반해 제한된 횟수의 연산만 수행할 수 있는 암호는 제한동형암호(somewhat homomorphic encryption)라 부른다. 완전동형암호는 암호화된 상태의 데이터에 대해서도 컴퓨터로 할 수 있는 모든 연산을 원하는 대로 수행할 수 있으므로 검색이나 통계적인 분석뿐 아니라 기계학습이나 영상처리 등 매우 복잡한 연산에도 적용할 수 있다. 개인정보를 기반으로 한 기계학습의 경우 암호화된 데이터상에서 분석을 수행하고 분석결과를 확인하는 마지막 단계에서만 복호화하여 개인정보 열람을 최소화할 수 있다. 완전동형암호는 컴퓨터가 하는 모든 연산을 암호화한 상태로도 수행할 수 있는 이론적 강점이 있지만 평문 연산보다 암호문 연산의 효율성에서는 떨어진다는 단점이 있다. 그러나 응용 연산의 종류에 따라 속도의 차이가 크기 때문에 개별 연산에 대해 최적화하여 적용하는 방법으로 효율성을 높일 수 있다. 또한 동형암호 연구가 아직 초기 단계이므로 알고리즘의 개발에 따라 효율이 크게 향상될 여지가 있다. 예를 들면, 동형암호 연산 중에 가장 비효율적인 재부팅 시간이 2011년도에는 30분이었던 것이 2013년에는 0.32초, 2015년에는 0.02초까지 계산속도가 빠르게 개선되고 있다.[4]
- 구현 원리
[5]원리 설명 부분 동형 암호
(SHE)- Somewhat homomorphic encryption(SHE), 덧셈과 곱셈 모두 지원(곱셈은 특정 횟수 K 번까지만 지원하도록 설계)
- ElGamal암호가 곱셈만 가능한 곱셈 동형 암호
스쿼싱
(Squashing)- 복호화 알고리즘 및 공개키 일부 변형
- 곱셈 k 회 이하만 적용 시 복호화 가능(복호화 알고리즘이 동형으로 계산 가능)
- 노이즈 증가 감소, 평문 변형되지 않도록 구성하는 원리
부트스트래핑
(Bootstrapping)- 암호화된 키와 이중 암호화된 암호문 입력한 후 복호화 알고리즘 실행, 새로운 암호문 생성(Recrypt), 동형 연산 후 매번 Recrypt 수행하여 FHE를 생성
- 암호문에 암호화된 비밀키를 이용하여 노이즈가 감소된 새로운 암호문 생성 후 연산 수행하는 설계원리
- 특성
[5]서킷 프라이버시 서킷 프라이버시는 연산 진행 시 연산에 대한 정보를 알지 못하는 성질이다. 다중 도약 동형성 다중 도약 동형성은 생성된 암호문이 다른 동형 연산의 입력으로 사용이 가능한 성질이다. 보안성 보안성은 암호화된 형태로 연산이 진행되어 해킹 차단할 수 있는 성질을 말한다.
- 격자 기반암호
- 동형암호는 암호체계 중 높은 난이도를 가졌다고 언급되는 격자 기반암호(lattice problem)의 한 종류이다. 3차원까지는 인간의 머릿속에서 이미지를 그릴 수 있지만 4차원부터는 오직 수식으로만 표현이 가능하다. 수백 차원의 격자 위의 임의 위치에서 가장 가까운 점을 찾기가 어렵다는 것을 근거로 하여 동형암호는 계산되는 데 엄청난 시간이 필요하고 양자 컴퓨터도 찾아내기 힘들다. 그로 인해 동형암호는 양자컴퓨팅의 보안 방법 중 하나로 주목받고 있다.[2]
- 성능 비교
- 공개키 암호와 동형암호의 성능 비교
[4]공개키
크기암호문
크기평문
크기암호화
시간복호화
시간덧셈
시간곱셈
시간허용
depth안전성 RSA 2048bit 2048bit - 6.1ms 205.5ms - - - - ECC 193bit 80B - 8.7ms 18.1ms - - - - Helib 343KB 105KB ≤1KB 17ms 6ms 0.6ms 54.3ms 6 128bit SEAL2.4v 2000KB 224KB ≤1KB 5.9ms 1.6ms 0.2ms 24ms 9 128bit HEAAN 80KB 96KB 16KB 43ms 12ms 5ms 100ms 6 128bit
종류[편집]
- 혜안(HeaAn)
- 혜안(HeaAn) 알고리즘은 천정희 교수가 설립한 '크립토 랩'에서 동형암호학 알고리즘을 획기적으로 개선한 알고리즘이다. 전산의 이론을 보면 비트 단위의 더하기와 곱하기를 실행할 수 있을 때, 실제로 컴퓨터가 하는 모든 연산을 수행할 수 있다는 증명할 수 있다. 이를 튜링 완전성이라고도 한다. 동형암호가 모든 것을 할 수 있다는 건 증명이 됐으나, 그것을 실용적으로 쓸 수 있는지 확인을 하기 위해서 데이터들을 더하는 32비트 데이터 여러 개를 덧셈과 곱셈 연산을 해보았을 때, 결과는 가능하지만, 속도가 너무 느리다는 결론이 나온다. 데이터를 곱하면 곱할수록 숫자가 다룰 수 없을 만큼 큰 크기가 돼버리기 때문이다. 숫자를 반올림하여 유효숫자가 아닌 숫자를 버리고 짧은 숫자들만 연산을 진행하는 것을 근사계산이라고 하는데 근사계산을 수행할 때, 연산마다 라운딩을 할 수 있도록 하여 다른 암호보다 월등히 좋은 성능을 보이게 된 것이다.[6]
- HELib
- HElib는 동형암호(HE)를 구현하는 소프트웨어 라이브러리이다. 현재 Smart-Vercauteren 암호문 패킹 기술과 Gentry-Halevi-Smart 최적화의 효과적인 사용에 주로 초점을 맞추어 동질성 평가를 빠르게 수행하는 많은 최적화와 함께 Brakerski-Gentry-Vaikuntanathan (BGV) 체계의 구현이 가능하다. 기본 암호 시스템은 동형에 적용 할 수 있는 일련의 운용을 정의하고 비용을 명시한다는 점에서 HElib의 '하드웨어 플랫폼'과 동일한 역할을 한다. 이 플랫폼은 SIMD 환경(Intel SSE 등과 유사)이지만 고유한 비용 지표와 매개변수를 가지고 있다. 동형 암호화를 위해 공개키가 구성되는 방식은 키 스위칭 매트릭스 때문에 비용이 많이 든다. 각 매트릭스는 공개키에 수 메가바이트를 추가하며, HElib에서는 공개키에 수백 개의 매트릭스가 있을 수 있다. 연구원들은 일반적인 작업에 대해 매트릭스의 크기를 33~50% 줄일 수 있다고 말한다. 또한, HElib는 연구 수준 프로젝트이며 유사 암호화를 위한 어셈블리 언어를 사용한다.[7][8]
- SEAL
- 마이크로소프트에서 만든 동형암호 라이브러리이다. [9]
장단점[편집]
- 장점
- 동형암호는 암호문을 복호화하지 않아도 검색, 통계 처리 및 기계 학습이 가능하고, 데이터를 처리하는 중간 과정에서 복호화하지 않아도 되므로, 데이터 유출 위험이 감소하는 장점이 있다.
- 단점
- 단점은 기존 암호의 확장률(평문 대비 암호문이 커지는 비율)에 비해 10배에서 100배 정도 커질 수 있고, 암복호화 속도가 1ms인 RSA 대비 수십 ms가 소요되며, 암호문 곱셈 연산의 경우, 수백ms가 소요된다. 한편 앞에서 언급했던 노이즈 감소를 위한 재부팅 시간이 필수적으로 필요하며, 2015년 기준 재부팅 시간이 0.02초 정도로 보고되었다.[10]
전망[편집]
동형암호는 의료 분야, 금융 분야 뿐만 아니라 블록체인과 양자컴퓨팅 분야에 활용할 수 있을 것으로 예상된다. 블록체인은 연산 과정을 모두 파악할 수 있는 특성이 있어 민감한 개인정보를 다루기 어려웠는데 동형 암호 기술을 활용한다면 효용성이 매우 상승할 것으로 기대된다. 또한 클라우드 기반 데이터 분석을 가능하게 하여 데이터를 활용하는 분야에 유용한 정보를 제공할 수 있을 것으로 전망된다.[2]
예시[편집]
- 삼성 SDS는 2019년 3월 14일 최근 기업들이 핵심업무까지 클라우드로 전환하면서 보안에 큰 관심을 기울이고 있어서 인공지능(AI) 기술을 접목한 보안관제서비스로 운영되는 클라우드 환경의 보안 공백을 '제로화' 하고, 정보의 흐름이나 보안 설정 등에 문제가 생기면 스스로 찾아서 차단해주는 정보 유출방지 서비스를 제공한다고 했다. 또한, 암호화된 데이터를 복호화하지 않고 그대로 분석해 결과까지 암호화된 상태로 제공하는 '동형암호' 기술을 연내 상용화할 계획이라고 했다. 덧붙여, 서울대학교 천정희 교수팀과 협력해 동형암호의 최대 난관인 분석속도 문제를 해소한 원천기술을 확보했고 이미 시범적으로 금융, 의료 등 민감한 데이터를 동형암호로 분석하는 데 성공해 현재도 실제 적용이 가능한 수준이라고 설명했다.[11]
- 생체인식
- 출입 통제에 사용하는 생체 정보를 안전하게 처리할 수 있다. 완전 동형암호화된 지문 등의 생체 정보를 복호화하지 않고, 암호화된 채로 인증을 수행할 수 있다면, 생체 정보를 복호화해 평문으로 보관하거나, 검증을 위해 원본을 전송할 필요 없이 받은 암호문과 보관 중인 암호화된 생체 정보를 비교해 일치 여부를 확인할 수 있도록 할 수 있다. 2018년 11월 '개인식별 방지 기술 세미나'에서 한국스마트인증(대표 문기봉)이 이러한 완전 동형암호기술을 활용해 홍채 인증 기술을 개량 발전 시켜 인증 시간을 0.25초로 앞당긴 시스템을 발표했다.
- 금융
- 완전 동형암호는 컴퓨터가 할 수 있는 연산을 모두 수행할 수 있어 데이터의 기밀성을 보호하면서 금융 데이터를 동형 기계 학습의 훈련 단계에서 활용할 수 있다. 동형 기계 학습의 훈련 단계에서 암호화된 데이터 연산을 통해 예측•분류 모형을 얻고 그 모형으로부터 실시간 계산이 필요한 예측 단계에서는 함수 암호를 사용한다. 동형 기계 학습은 데이터의 기밀성을 보호할 수 있어 개인의 민감한 정보의 유출에 대한 보안 문제를 해결할 수 있으며 데이터의 손실 없이 신용도 평가 예측 모형의 고도화가 가능하다고 할 수 있다. 실제 사례로, 2018년 11월 ‘개인식별 방지 기술 세미나’에서 코리아크레딧뷰로(KCB, 대표 강문호)는 50만 명의 신용 데이터를 동형암호화된 상태에서 기계 학습을 수행해 개인정보를 보호하면서 신용 평가 모형의 신뢰성, 정확성, 안전성을 성공적으로 확보할 수 있음을 검증했다.[10]
각주[편집]
- ↑ 개인정보보호, 〈안전한 개인정보 활용을 위한 동형 암호〉, 《네이버 블로그》, 2019-02-08
- ↑ 2.0 2.1 2.2 과학기술정보통신부, 〈4세대 암호, '동형암호'를 소개합니다!〉, 《네이버 블로그》, 2019-04-19
- ↑ IMDARC, 〈암호기술 혁명 - 동형암호〉, 《IMDARC》, 2018-10-26
- ↑ 4.0 4.1 4.2 천정희, 어윤희, 김재윤, 〈개인정보가 보호되는 동형암호기반 금융데이터분석〉, 《한국금융정보학회》, 2019-02-28
- ↑ 5.0 5.1 기술사를위해, 〈동형암호〉, 《네이버 블로그》, 2019-05-03
- ↑ HASHED, 〈해시드 인터뷰: 서울대학교 천정희 교수 (Jung-hee Cheon), 동형암호와 블록체인〉, 《Medium》, 2019-05-22
- ↑ Richard Chirgwin, 〈IBM's homomorphic encryption accelerated to run 75 times faster〉, 《The Register》, 2018-03-08
- ↑ GitHub 공식 홈페이지 - 〈HElib〉
- ↑ GitHub 공식 홈페이지 - 〈SEAL〉
- ↑ 10.0 10.1 LG CNS, 〈4세대 암호, 완전동형암호란?〉, 《LG CNS 블로그》, 2019-07-16
- ↑ 남도영, 〈삼성SDS, 비밀병기 '동형암호'로 클라우드 보안 '자신감'〉, 《msn 뉴스》, 2019-03-14
참고자료[편집]
- 개인정보보호, 〈안전한 개인정보 활용을 위한 동형 암호〉, 《네이버 블로그》, 2019-02-08
- 과학기술정보통신부, 〈4세대 암호, '동형암호'를 소개합니다!〉, 《네이버 블로그》, 2019-04-19
- 기술사를위해, 〈동형암호〉, 《네이버 블로그》, 2019-05-03
- IMDARC, 〈암호기술 혁명 - 동형암호〉, 《IMDARC》, 2018-10-26
- 천정희, 어윤희, 김재윤, 〈개인정보가 보호되는 동형암호기반 금융데이터분석〉, 《한국금융정보학회》, 2019-02-28
- HASHED, 〈해시드 인터뷰: 서울대학교 천정희 교수 (Jung-hee Cheon), 동형암호와 블록체인〉, 《Medium》, 2019-05-22
- Richard Chirgwin, 〈IBM's homomorphic encryption accelerated to run 75 times faster〉, 《The Register》, 2018-03-08
- GitHub 공식 홈페이지 - 〈HElib〉
- GitHub 공식 홈페이지 - 〈SEAL〉
- 남도영, 〈삼성SDS, 비밀병기 '동형암호'로 클라우드 보안 '자신감'〉, 《msn 뉴스》, 2019-03-14
- LG CNS, 〈4세대 암호, 완전동형암호란?〉, 《LG CNS 블로그》, 2019-07-16
같이 보기[편집]

 위키원
위키원