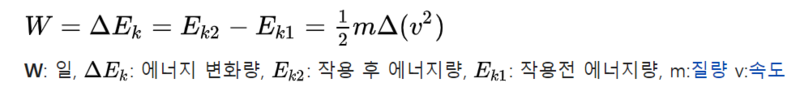"일 (물리)"의 두 판 사이의 차이
잔글 (→같이 보기) |
|||
| (사용자 2명의 중간 판 3개는 보이지 않습니다) | |||
| 8번째 줄: | 8번째 줄: | ||
일은 일반적으로 힘이 가해진 방향으로 움직인 물체의 거리로 정의된다. 이렇게 정의할 때 일은 단순히 다음의 식으로 나타낼 수 있다. | 일은 일반적으로 힘이 가해진 방향으로 움직인 물체의 거리로 정의된다. 이렇게 정의할 때 일은 단순히 다음의 식으로 나타낼 수 있다. | ||
| − | '''''W = F ∙ d = Fd cos θ ''''' W: 일, F: 힘, d: 거리 또는 '''''W = F ∙ s''''' W: 일, F: 힘, s: 힘의 방향으로 이동한 거리로도 나타낼 수 있다. | + | '''''W = F ∙ d = Fd cos θ ''''' W: 일, F: 힘, d: 거리 |
| + | |||
| + | 또는 '''''W = F ∙ s''''' W: 일, F: 힘, s: 힘의 방향으로 이동한 거리로도 나타낼 수 있다. | ||
이 때, 힘은 방향성을 갖는 벡터 양이기 때문에, 위에서 설명한 식은 엄밀하게는 힘과 변위(變位, 위치의 변화) 벡터의 스칼라 곱의 선적분으로 정의되어야 한다. 엄밀하게 정의된 일은 다음의 식으로 나타낼 수 있다. | 이 때, 힘은 방향성을 갖는 벡터 양이기 때문에, 위에서 설명한 식은 엄밀하게는 힘과 변위(變位, 위치의 변화) 벡터의 스칼라 곱의 선적분으로 정의되어야 한다. 엄밀하게 정의된 일은 다음의 식으로 나타낼 수 있다. | ||
| 38번째 줄: | 40번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[일]] | ||
| + | * [[물리]] | ||
* [[줄]] | * [[줄]] | ||
* [[줄의 법칙]] | * [[줄의 법칙]] | ||
| 43번째 줄: | 47번째 줄: | ||
* [[일률]] | * [[일률]] | ||
| − | {{ | + | {{물리|검토 필요}} |
2023년 1월 23일 (월) 15:23 기준 최신판
일(Work)은 물리학에서 물체에 힘을 가했을 때 힘과 힘이 가해진 방향으로 움직인 거리를 곱한 물리량을 뜻한다. 일의 단위는 줄이다. 한편, 일-에너지 따라 작용을 통해 힘에 의해 변환된 에너지의 총합으로 표현할 수 도 있다.
개요[편집]
일은 스칼라 양이고 양의 일 또는 음의 일이 가능하다. 힘의 방향과 물체의 운동 방향이 같을 때 양의 일을 하고 반대일 때는 음의 일을 한다. 힘이 가해졌다 하더라도 일은 0이 될 수도 있다. 예를 들면 등속 원운동에서 구심력이 하는 일은 언제나 0이다. 등속원운동에서는 구심력이 주어지는 방향과 물체가 움직이는 방향이 언제나 직각이기 때문이다.(즉, 가해진 힘에 대해 물체의 이동거리가 0이기 때문이다.) 이것은 다시 에너지의 변화로도 설명될 수 있다. 등속원운동에서는 구심력에 의한 물체의 에너지 변화가 없기 때문에 일은 0이다. 또한 단순히 일의 공식 W = F ∙ d = Fd cos θ 에서 θ = π/2 이기 때문에 cos θ = 0 이 되어 W=0 이 성립하기도 한다.
정의[편집]
힘과 거리의 곱[편집]
일은 일반적으로 힘이 가해진 방향으로 움직인 물체의 거리로 정의된다. 이렇게 정의할 때 일은 단순히 다음의 식으로 나타낼 수 있다.
W = F ∙ d = Fd cos θ W: 일, F: 힘, d: 거리
또는 W = F ∙ s W: 일, F: 힘, s: 힘의 방향으로 이동한 거리로도 나타낼 수 있다.
이 때, 힘은 방향성을 갖는 벡터 양이기 때문에, 위에서 설명한 식은 엄밀하게는 힘과 변위(變位, 위치의 변화) 벡터의 스칼라 곱의 선적분으로 정의되어야 한다. 엄밀하게 정의된 일은 다음의 식으로 나타낼 수 있다.
물체에 작용하는 힘이 보존력(conservative force)이면 물체에 해준 일은 처음 위치와 나중 위치에 의해서만 결정되고, 경로에 관계없다.
물체에 작용하는 알짜힘이 그 물체에 해준 일은 물체의 운동에너지 변화와 같다. 이를 일·운동에너지 정리 또는 일·에너지 정리라고 하며, 물체에 작용하는 힘에 대한 구체적인 정보가 없어도, 그 힘이 해준 일을 알아내는 데 아주 유용하다.
힘에 의해 변화된 에너지의 총합[편집]
일-에너지 이론에 의하면 일은 작용을 통해 힘에 의해 변환된 에너지의 총합으로 정의할 수 있다. 이렇게 정의할 때 일은 다음의 식으로 나타낼 수 있다.
단위[편집]
일의 SI 유도 단위는 1 뉴턴의 힘이 1 미터의 거리를 이동하게 하는 일로 정의한, 줄(J)이다.
J = N ∙ m
J: 줄, N: 뉴턴, m: 미터
일의 원리[편집]
어떠한 도구를 사용하더라도 결국 물체에 한 일의 크기는 같다.
또, 도르래 등을 사용해 힘을 적게 쓰도록 할 수는 있지만, 힘이 가해진 거리가 늘어나야 하기 때문에 한 일의 양, 즉 소모한 에너지를 보았을 때에는 이득은 없다.
참고자료[편집]
같이 보기[편집]
| ||||||||||||||||||||||||||||||

 위키원
위키원