"축바퀴"의 두 판 사이의 차이
(새 문서: 썸네일|300픽셀|축바퀴의 예-윈들러스 '''축바퀴'''는 반지름이 서로 다른 두 개의 회전체를 한 중심축에 고정시켜 회...) |
잔글 (→상세) |
||
| (같은 사용자의 중간 판 하나는 보이지 않습니다) | |||
| 7번째 줄: | 7번째 줄: | ||
큰 바퀴가 작은 바퀴를 중심으로 연결되어 있는 형태이다. 물체는 작은 바퀴 쪽에, 잡아 당기는 줄은 큰 바퀴 쪽에 연결한다. 지레의 원리를 응용한 장치이기 때문에 힘점, 작용점, 받침점이 존재하는데, 힘이 가해지는 부분, 즉 잡아 당기는 줄이 연결된 큰 바퀴가 힘점이 된다. 또한 힘이 작용하는 부분, 즉 물체가 연결된 작은 바퀴가 작용점이 되며, 마지막으로 축의 중심은 받침점이 된다. | 큰 바퀴가 작은 바퀴를 중심으로 연결되어 있는 형태이다. 물체는 작은 바퀴 쪽에, 잡아 당기는 줄은 큰 바퀴 쪽에 연결한다. 지레의 원리를 응용한 장치이기 때문에 힘점, 작용점, 받침점이 존재하는데, 힘이 가해지는 부분, 즉 잡아 당기는 줄이 연결된 큰 바퀴가 힘점이 된다. 또한 힘이 작용하는 부분, 즉 물체가 연결된 작은 바퀴가 작용점이 되며, 마지막으로 축의 중심은 받침점이 된다. | ||
| − | [[파일:축바퀴의 돌림힘.jpg|썸네일| | + | [[파일:축바퀴의 돌림힘.jpg|썸네일|300픽셀|]] |
큰 바퀴의 반지름을 R, 작은 바퀴의 반지름을 r이라 하고, 축바퀴에 가하는 힘을 F, 들어올리는 물체의 중량을 w라 할 때, 큰 바퀴에 작용하는 돌림힘과 작은 바퀴에 작용하는 돌림힘의 크기는 각각 다음과 같다. | 큰 바퀴의 반지름을 R, 작은 바퀴의 반지름을 r이라 하고, 축바퀴에 가하는 힘을 F, 들어올리는 물체의 중량을 w라 할 때, 큰 바퀴에 작용하는 돌림힘과 작은 바퀴에 작용하는 돌림힘의 크기는 각각 다음과 같다. | ||
| 23번째 줄: | 23번째 줄: | ||
[[파일:큰바퀴, 작은바퀴, 축으로 이루어진 축바퀴.png|썸네일|300픽셀|큰바퀴, 작은바퀴, 축으로 이루어진 축바퀴]] | [[파일:큰바퀴, 작은바퀴, 축으로 이루어진 축바퀴.png|썸네일|300픽셀|큰바퀴, 작은바퀴, 축으로 이루어진 축바퀴]] | ||
[[파일:큰바퀴와 작은바퀴에 가해지는 힘과 원주속도.png|썸네일|300픽셀|큰바퀴와 작은바퀴에 가해지는 힘과 원주속도]] | [[파일:큰바퀴와 작은바퀴에 가해지는 힘과 원주속도.png|썸네일|300픽셀|큰바퀴와 작은바퀴에 가해지는 힘과 원주속도]] | ||
| + | [[파일:축바퀴의 힘점, 받침점, 작용점.png|썸네일|300픽셀|축바퀴의 힘점, 받침점, 작용점]] | ||
일반적으로 [[축]]과 [[바퀴]]는 이동이나 운송을 용이하게 하는데 주로 사용하는데 축과 바퀴를 효율적으로 사용하면 작은 힘으로 큰 힘을 전달할 수 있어요. 무거운 물체를 들거나 물체가 견디는 저항을 이겨서 힘의 이득을 얻을 수 있다. | 일반적으로 [[축]]과 [[바퀴]]는 이동이나 운송을 용이하게 하는데 주로 사용하는데 축과 바퀴를 효율적으로 사용하면 작은 힘으로 큰 힘을 전달할 수 있어요. 무거운 물체를 들거나 물체가 견디는 저항을 이겨서 힘의 이득을 얻을 수 있다. | ||
| 54번째 줄: | 55번째 줄: | ||
===축바퀴 = 회전하는 지렛대(지레)=== | ===축바퀴 = 회전하는 지렛대(지레)=== | ||
| − | |||
축바퀴는 회전하는 지레로 볼 수 있습니다. 초록색 화살표는 힘 F, 빨간색 화살표는 하중 W를 나타낸다. 물체의 무게나 물체가 견디는 저항을 하중이라고 한다. 축바퀴의 중심이 받침점이 되고 힘 F가 가해지는 큰 바퀴가 힘점, 하중 W가 걸리는 작은 바퀴가 작용점이 된다. | 축바퀴는 회전하는 지레로 볼 수 있습니다. 초록색 화살표는 힘 F, 빨간색 화살표는 하중 W를 나타낸다. 물체의 무게나 물체가 견디는 저항을 하중이라고 한다. 축바퀴의 중심이 받침점이 되고 힘 F가 가해지는 큰 바퀴가 힘점, 하중 W가 걸리는 작은 바퀴가 작용점이 된다. | ||
2024년 8월 28일 (수) 16:30 기준 최신판
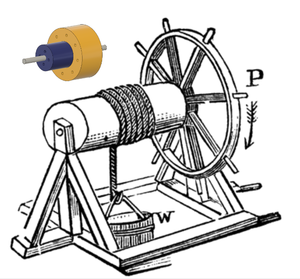
축바퀴는 반지름이 서로 다른 두 개의 회전체를 한 중심축에 고정시켜 회전할 수 있게 만든 것. 중심축을 회전시키면 두 회전체의 각 속도는 일정하게 회전하지만 회전하는 거리는 반지름에 따라 다르다. 즉, 반지름이 큰 회전체가 더 많은 거리를 회전하게 된다. 이 현상을 적은 힘을 들이고 일을 할 수 있는 도구에 이용할 수 있다. 반지름이 두 배인 회전체를 이용하면 절반 정도의 힘으로 물체를 움직일 수 있다. 축바퀴를 이용한 대표적인 도구가 드라이버이다. 드라이버의 손잡이가 굵을수록 적은 힘으로 나사를 조일 수 있다.
개요[편집]
지름이 다른 두 바퀴를 하나의 축에 고정시킨 장치.
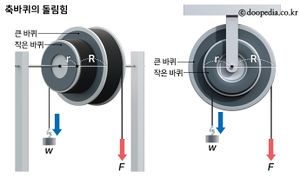
큰 바퀴가 작은 바퀴를 중심으로 연결되어 있는 형태이다. 물체는 작은 바퀴 쪽에, 잡아 당기는 줄은 큰 바퀴 쪽에 연결한다. 지레의 원리를 응용한 장치이기 때문에 힘점, 작용점, 받침점이 존재하는데, 힘이 가해지는 부분, 즉 잡아 당기는 줄이 연결된 큰 바퀴가 힘점이 된다. 또한 힘이 작용하는 부분, 즉 물체가 연결된 작은 바퀴가 작용점이 되며, 마지막으로 축의 중심은 받침점이 된다.
큰 바퀴의 반지름을 R, 작은 바퀴의 반지름을 r이라 하고, 축바퀴에 가하는 힘을 F, 들어올리는 물체의 중량을 w라 할 때, 큰 바퀴에 작용하는 돌림힘과 작은 바퀴에 작용하는 돌림힘의 크기는 각각 다음과 같다.
큰 바퀴에 작용하는 돌림힘 = R x F
작은 바퀴에 작용하는 돌림힘 = r x w
또한 회전축을 중심으로 큰 바퀴에 작용한 돌림힘과 작은 바퀴에 작용하는 돌림힘의 크기는 동일하므로, R x F = r x w임을 알 수 있다.
즉, 축바퀴는 돌림힘을 이용하여 본래 들여야 하는 힘보다 적은 힘으로 물체를 들어올릴 수 있는 장치이며, 이때 물체를 움직이는데 필요한 힘은 두 축바퀴의 반지름의 비율에 의해 결정된다. 작은 바퀴와 큰 바퀴의 반지름 비율이 1:2라면 물체의 무게의 1/2에 해당하는 힘만 가해줘도 물체를 움직일 수 있는 것이다. 이처럼 적은 힘으로도 무거운 물체를 움직일 수 있는 것을 힘의 이득이라고 한다. 하지만 물체의 이동 거리에 비례하여 당겨야 하는 줄의 이동 거리가 늘어나므로, 일의 양에는 변화가 없다.
수도꼭지나 연필깎이 손잡이, 문의 손잡이 등이 축바퀴 원리가 적용된 대표적인 예이다.
상세[편집]
일반적으로 축과 바퀴는 이동이나 운송을 용이하게 하는데 주로 사용하는데 축과 바퀴를 효율적으로 사용하면 작은 힘으로 큰 힘을 전달할 수 있어요. 무거운 물체를 들거나 물체가 견디는 저항을 이겨서 힘의 이득을 얻을 수 있다.
축바퀴는 지름이 다른 두 개의 바퀴가 중심이 같은 축과 함께 회전하면서 힘을 한 바퀴에서 다른 바퀴로 전달하는 단순 기계이다.
축바퀴의 원리[편집]
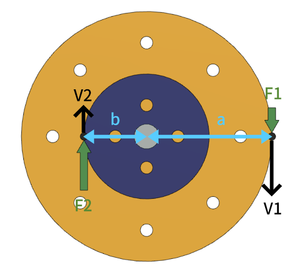
축의 중심에서 큰 바퀴 가장자리인 원주상의 한 점까지의 거리(큰 바퀴의 반경)를 a, 작은 바퀴의 원주상 한 점까지의 거리(작은 바퀴의 반경)를 b라 하고, 큰 바퀴의 원주상 한 점에 접선방향으로 힘 F1이 가해져서 V1의 원주 속도로 회전하면, 작은 바퀴의 원주상 한 점에 접선방향으로 F2가 전달되어 V2의 원주 속도로 회전한다.
축바퀴가 에너지를 방출하거나 저장하지 않는다고 가정하면, 즉 마찰이나 탄성이 없다고 가정한다.
에너지 보존의 법칙에 따라 큰 바퀴에 가해지는 힘에 의해 입력된 동력(P1)은 작은 바퀴에서 출력되는 동력(P2)과 같아야 한다.
동력 P는 단위 시간 t동안 한 일의 양 Q이다. 다음과 같이 동력은 힘과 속도의 곱으로 계산할 수 있다.
- 일의 양 Q = 힘 * 움직인 거리 = F * S
- 동력 P = Q / t = (F * S) / t =F * (S / t) = F * V
에너지 보존의 법칙에 따라,
- P1 = P2 이므로 F1 * V1 = F2 * V2
축바퀴를 회전시키면 축을 중심으로 두 바퀴가 함께 회전한다. 따라서 두 바퀴가 단위시간 t동안에 회전한 각도(=각속도)는 같다. 동영상을 보면 축바퀴는 10초 동안 90도를 회전한다. 큰 바퀴의 각속도 = 작은 바퀴의 각속도 = 90도/10초 = 9 deg/s로 모두 같다.
하지만 두 바퀴의 원주상에 있는 각 점이 회전하는 거리를 비교해보면 차이가 있다. 큰 바퀴의 점이 작은 바퀴의 점보다 더 긴 거리를 회전하게 된다. 각속도가 같아야 하므로 큰 바퀴의 원주상에 있는 한 점은 작은 바퀴의 원주상에 있는 한 점보다 더 빠르게 움직인다. 즉 큰 바퀴의 원주 속도 V1이 작은 바퀴의 원주 속도 V2보다 커야 한다. 이렇게 축바퀴가 회전할 때 큰 바퀴의 V1 > 작은 바퀴의 V2가 된다.
에너지 보존의 법칙에 따라 F1 * V1 = F2 * V2 가 되려면 F2 > F1 이 되어야 한다.
즉 큰 바퀴로 가해지는 힘 F1보다 작은 바퀴로 전달되는 힘 F2가 커지게 된다. 이 때문에 F2와 F1의 차이만큼 힘의 이득을 얻을 수 있는 것이다.
- 힘의 이득 = F2 - F1
축바퀴와 같이 단순 기계에서 힘의 이득은 입력한 힘 F1과 출력되는 힘 F2의 차이로 계산된다. 힘의 이득 = F2 - F1이 된다. 두 바퀴의 반경(a와 b) 차이를 크게 하면 어떻게 될까? 출력되는 힘과 입력한 힘의 차이가 더 커지고 힘의 이득은 더 커질 것이다.
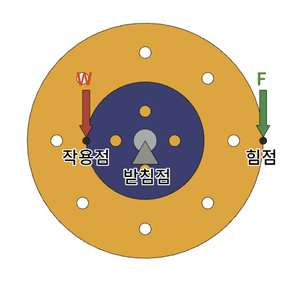
축바퀴 = 회전하는 지렛대(지레)[편집]
축바퀴는 회전하는 지레로 볼 수 있습니다. 초록색 화살표는 힘 F, 빨간색 화살표는 하중 W를 나타낸다. 물체의 무게나 물체가 견디는 저항을 하중이라고 한다. 축바퀴의 중심이 받침점이 되고 힘 F가 가해지는 큰 바퀴가 힘점, 하중 W가 걸리는 작은 바퀴가 작용점이 된다.
따라서 큰 바퀴의 힘점에 가해지는 힘 F는작은 바퀴의 하중 W이 걸려 있는 작용점으로 더 큰 힘을 전달하여, 작은 힘으로 무거운 물체를 들어 올릴 수 있는 것이다.
축바퀴의 실생활 응용 사례[편집]
축바퀴의 첫 번째 실생활 응용 사례 중 하나는 항아리를 제작하는 데 사용했던 도공의 물레가 있다. 도자기를 만들 때, 흙을 빚거나 무늬를 넣는 데 사용하는 기구를 물레라고 하는데 도공의 물레는 때때로 "도예가의 선반"으로 불리기도 한다.
- 윈들러스
중량물을 옮길 때 사용하는 윈들러스 또한 축바퀴의 잘 알려진 응용 사례이다. 우물에서 양동이와 같은 무거운 물체를 들어 올릴 때, 물체의 무게보다 더 작은 힘으로 들어 올릴 수 있도록 작은 바퀴에 로프를 감고 손잡이가 달린 큰 바퀴를 붙여서 사용한 단순 기계이다.
- 태엽키
T형 태엽키의 손잡이 부분이 클수록 더 적은 힘으로 태엽 스프링을 감을 수 있다. 손잡이는 큰 바퀴, 스프링을 감는 부분은 작은 바퀴가 된다.
- 열쇠 손잡이
자물쇠를 잠그거나 여는 데 사용하는 열쇠는 손잡이가 클수록 자물쇠를 더 작은 힘으로 열수 있다. 손잡이는 큰 바퀴, 열거나 잠그는 부분은 작은 바퀴가 된다.
- 스크루 드라이버
나사를 죄거나 푸는 데 사용하는 스크루 드라이버는 손잡이가 굵을수록 더 작은 힘으로 나사를 조일 수 있다. 손잡이는 큰 바퀴, 나사를 조이거나 푸는 날 끝은 작은 바퀴가 된다.
- 코르크 따개
와인의 코르크를 빼는 T형 코르크 따개로 손잡이가 길수록 코르크에 나선형 스크루를 더 작은 힘으로 조일 수 있다. 손잡이는 큰 바퀴, 나선형 스크루는 작은 바퀴가 된다.
- 스패너
볼트, 너트, 나사 등의 머리를 죄거나 푸는 공구로 스패너의 길이가 길수록 더 작은 힘으로 조일 수 있다. 스패너의 길이는 큰 바퀴, 스패너의 입구는 작은 바퀴가 된다.
- 육각 렌치
볼트 머리에 6각의 홈이 있는 볼트나 나사를 조이거나 풀 때 사용하는 공구로렌치의 길이가 길수록 더 작은 힘으로 조이거나 풀 수 있다. 손으로 잡는 부분은 큰 바퀴 , 6각 홈에 끼우는 부분은 작은 바퀴가 된다.
- 문 손잡이
문을 열고 닫기 위한 손잡이로 손잡이가 길수록 더 작은 힘으로 손잡이를 돌릴 수 있다. 손잡이는 큰 바퀴, 문을 열거나 닫는 부분은 작은 바퀴가 된다.
- 깡통 따개
깡통의 뚜껑을 따는 데 쓰는 깡통 따개는 손잡이가 클수록 더 적은 힘으로 쉽게 딸 수 있다. 손잡이가 큰 바퀴, 뚜껑을 감는 부분은 작은 바퀴가 된다.
- 핸드 드릴(수동 드릴)
손으로 핸들을 돌려 구멍을 뚫는 공구로 핸들이 클수록 구멍을 뚫을 때 더 작은 힘이 필요하다. 손잡이가 달린 크랭크는 큰 바퀴, 베벨 기어는 작은 바퀴가 된다.
- 연필깎이
연필을 깎는 데에 쓰는 기구로 손잡이가 길수록 더 작은 힘으로 연필을 깎을 수 있다. 손잡이는 큰 바퀴, 연필을 중심으로 회전하는 날은 작은 바퀴가 된다.
- 수도꼭지
수돗물을 나오게 하거나 막는 장치로 손잡이가 클수록 더 작은 힘으로 밸브를 열거나 닫을 수 있다. 손잡이는 큰 바퀴, 밸브를 여닫는 나사산 부분은 작은 바퀴가 된다.
- 자전거 페달
페달을 돌리는 크랭크가 큰 바퀴, 체인이 감긴 톱니바퀴가 작은 바퀴가 된다. 톱니바퀴가 작을수록 페달을 밟는 힘은 덜 들지만, 한번 페달링으로 가는 거리도 줄어든다.
- 낚시릴
낚싯대 밑부분에 달아서 낚싯줄을 풀거나 감을 수 있게 만든 장치로 손잡이가 클수록 더 작은 힘으로 빨리 풀거나 감을 수 있다. 손잡이는 큰 바퀴, 줄을 풀거나 감아주는 부분(스풀 또는 베일)은 작은 바퀴가 된다.
- 자동차 핸들
자동차의 방향을 전환하는 장치로 핸들이 클수록 더 작은 힘으로 돌릴 수 있다. 조향 핸들은 큰 바퀴, 조향축에 연결된 조향기어는 작은 바퀴가 된다.
참고자료[편집]
- 〈축바퀴〉, 《Basic 중학생이 알아야 할 사회· 과학상식》
- 〈축바퀴〉, 《두산백과》
- CRK, 〈회전하는 지렛대(지레)~축바퀴의 개념, 원리, 실생활 응용 사례〉, 《네이버 블로그》, 2023-01-07
같이 보기[편집]

 위키원
위키원