"리처드 파인만"의 두 판 사이의 차이
| 32번째 줄: | 32번째 줄: | ||
1986년 1월에는 7명의 승무원을 태운 우주왕복선 챌린저호가 폭발하여 승무원 전원이 사망하는 사건이 발생하였는데, 대통령의 명령에 의해 구성된 조사 위원회에서 파인만은 논리적 추론만으로 사고의 원인을 알아내었다. 사고의 원인이 오링(O-ring)이라는 부품에 있었음을 밝혀내었는데, 고체 로켓 부스터에 사용된 고무 재질인 오링이 추운 날씨로 인해 탄력을 잃으면서 고온 고압의 가스가 오링 사이로 누출되었고 그에 불이 붙으면서 폭발한 것이었다. 이 사건을 통해 파인만은 천재 물리학자라는 호칭이 헛된 것이 아님을 다시 한번 증명해내었다.<ref name="지식백과"></ref><ref name="팔방미인></ref><ref name="논문"></ref> | 1986년 1월에는 7명의 승무원을 태운 우주왕복선 챌린저호가 폭발하여 승무원 전원이 사망하는 사건이 발생하였는데, 대통령의 명령에 의해 구성된 조사 위원회에서 파인만은 논리적 추론만으로 사고의 원인을 알아내었다. 사고의 원인이 오링(O-ring)이라는 부품에 있었음을 밝혀내었는데, 고체 로켓 부스터에 사용된 고무 재질인 오링이 추운 날씨로 인해 탄력을 잃으면서 고온 고압의 가스가 오링 사이로 누출되었고 그에 불이 붙으면서 폭발한 것이었다. 이 사건을 통해 파인만은 천재 물리학자라는 호칭이 헛된 것이 아님을 다시 한번 증명해내었다.<ref name="지식백과"></ref><ref name="팔방미인></ref><ref name="논문"></ref> | ||
| − | ==업적== | + | ==주요 업적== |
*중성자 성질에 대한 이론적 규명 | *중성자 성질에 대한 이론적 규명 | ||
*양자 전기 역학의 재규격화를 이루어 내었고, 이로 인해 노벨물리학상을 수상하였다. | *양자 전기 역학의 재규격화를 이루어 내었고, 이로 인해 노벨물리학상을 수상하였다. | ||
| 38번째 줄: | 38번째 줄: | ||
*경로적분 제안 | *경로적분 제안 | ||
*원주율 소수 762~767 자리에서 9가 연속으로 6번 나옴을 발견해냄(파인만 포인트)<ref>리처드 파인만 위키백과 - https://ko.wikipedia.org/wiki/%EB%A6%AC%EC%B2%98%EB%93%9C_%ED%8C%8C%EC%9D%B8%EB%A7%8C</ref> | *원주율 소수 762~767 자리에서 9가 연속으로 6번 나옴을 발견해냄(파인만 포인트)<ref>리처드 파인만 위키백과 - https://ko.wikipedia.org/wiki/%EB%A6%AC%EC%B2%98%EB%93%9C_%ED%8C%8C%EC%9D%B8%EB%A7%8C</ref> | ||
| + | ===파인만 다이어그램=== | ||
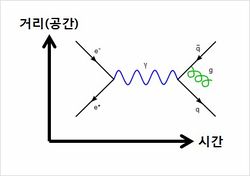
| + | 리처드 파인만이 도입한 파인만 다이어그램은 양자장에서 입자들의 변화를 쉽게 표현해주는 그림이다. 양자장론에서 이 다이어그램을 통해 전이진폭 혹은 상관 함수의 계산에서 나타나는 항들을 나타내는 도형이며, 시공간 다이어그램이다. 하나의 물리적 과정은 아래에서 시작하여 위에서 또는 왼쪽에서 시작하여 오른쪽에서 끝난다. 다이어그램의 모든 선은 입자를 나타내는데, 세 가지 유형의 기본입자가 존재한다. 세 개의 선이 만나는 정점은 전자기의 상호작용을 의미한다.[[파일:파인만 다이어그램.JPG|250픽셀|오른쪽|썸네일|파인만 다이어그램]] | ||
| + | |||
| + | 양자장론의 정준 수식화에서 파인만 다이어그램은 산란 행렬의 윅의 정리에 따른 섭동 이론적 전개에서의 특정 항을 나타낸다. 이때 전이진폭은 양자계의 시작과 끝 사이의 상태에 대한 산란 행렬의 성분이다. 경로 적분의 관점에서 보면, 전이진폭은 계의 처음과 마지막 상태 사이의 모든 가능한 경로들의 합이다. 파인만 다이어그램은 성분이 결합하고 쪼개어지는 그림을 통해 입자의 특정 경로를 직관적으로 나타낸다. | ||
| + | |||
| + | ;규칙 | ||
| + | 입자의 전파인지는 변이고, 입자 사이의 상호작용은 꼭짓점으로 나타낸다. | ||
| + | 입자가 그 반입자와 다를 경우, 그 변은 유향(directed) 변이고, 화살표로 방향을 표시한다. 입자의 경우에는 초기 상태에서 최종 사태를 향하여 가리키고, 반입자는 최종 상태에서 초기 상태를 가리킨다. 입자가 그 반입자와 같은 경우에는 화살표로 표시하지 않으며, 광자와 W 및 Z 보손은 물결선으로 나타낸다. 글루온은 꼬인 선으로 나타내고, 기타 입자를 구별할 필요가 있다면 변 옆에 부호로 표현한다.<ref>파인만 도형 위키 백과 - https://ko.wikipedia.org/wiki/%ED%8C%8C%EC%9D%B8%EB%A7%8C_%EB%8F%84%ED%98%95</ref><ref>soma0sd, 〈[http://blog.naver.com/sw2045/110171827813 파인만 다이어그램 (파인만 도형)]〉, 《네이버 블로그》, 2013-07-10</ref><ref>정계섭, 〈[http://www.ndsl.kr/ndsl/commons/util/ndslOriginalView.do?dbt=JAKO&cn=JAKO200606140723240&oCn=JAKO200606140723240&pageCode=PG11&journal=NJOU00294661 도형에 의한 추론 (Schematic Reasoning) : 통시적 사례 연구]〉, 《덕성여대》, 2006-11</ref> | ||
| + | |||
| + | ===QED=== | ||
| + | QED는 전자와 빛을 양자 현상으로 다룬다. 양자라는 개념은 20세기 들어서면서 나타났다. 그 당시에, QED는 과학자들에게 숙제와도 같은 것이었는데, 디랙과 슈뢰딩거가 방정식을 만들어내면서 성공하는 듯 싶었다. 하지만 무한대의 양이 출현 함으로써 문제가 발생하였고, 제2차 세계대전이 끝난 이후에 셸터 아일랜드 학회에서 과학자들이 모여 연구를 시작했다. 학회가 끝나고 슈윙거가 이 문제를 해결해내었지만, 그 과정이 너무나 복잡하고 어려워 다른 사람들이 이해하기에 어려움을 겪었다. 그런데 파인만은 슈윙거와는 다른 방식으로 이 문제에 대해 접근하였다. 그는 시공간의 한 점에서 다른 점으로 입자가 전파하는 방식으로 전자의 움직임을 파악하고자 했다. 여기서 파인만은 길적분이라는 아이디어를 도입하여 그 당시에 문제가 되었던 디랙 방정식과 슈뢰딩거 방정식의 충돌을 해결하였고, 이러한 방식은 기존의 슈윙거가 만든 방법보다 간단하고 빠르며, 눈에 보이는 방식으로 구할 수 있어 이해하기에 편리하였다.<ref>임채호, 〈[http://webzine.kps.or.kr/contents/data/webzine/webzine/14762087792.pdf QED가 완성되기까지의 역사와 의미]〉, 2015-05</ref> | ||
| + | |||
==주요 저서== | ==주요 저서== | ||
| 59번째 줄: | 71번째 줄: | ||
*〈[http://www.kyobobook.co.kr/author/info/AuthorInfo.laf?mallGb=EAU&authorid=2000006601&orderClick=JFX 리처드 파인만]〉, 《교보문고》 | *〈[http://www.kyobobook.co.kr/author/info/AuthorInfo.laf?mallGb=EAU&authorid=2000006601&orderClick=JFX 리처드 파인만]〉, 《교보문고》 | ||
*안종주, 〈[http://www.ndsl.kr/ndsl/commons/util/ndslOriginalView.do?dbt=JAKO&cn=JAKO201467352676550&oCn=JAKO201467352676550&pageCode=PG11&journal=NJOU00296711 <파인만의 물리학 강의>의 리처드 파인만]〉, 2014 | *안종주, 〈[http://www.ndsl.kr/ndsl/commons/util/ndslOriginalView.do?dbt=JAKO&cn=JAKO201467352676550&oCn=JAKO201467352676550&pageCode=PG11&journal=NJOU00296711 <파인만의 물리학 강의>의 리처드 파인만]〉, 2014 | ||
| + | *임채호, 〈[http://webzine.kps.or.kr/contents/data/webzine/webzine/14762087792.pdf QED가 완성되기까지의 역사와 의미]〉, 2015-05 | ||
*whatx4, 〈[https://whatx4.tistory.com/73 리처드 파인만(Richard P. Feynman) 잠언, 명언, 인용 - 1]〉, 《티스토리》, 2016-10-10 | *whatx4, 〈[https://whatx4.tistory.com/73 리처드 파인만(Richard P. Feynman) 잠언, 명언, 인용 - 1]〉, 《티스토리》, 2016-10-10 | ||
*Soo , 〈[https://m.blog.naver.com/PostView.nhn?blogId=miseos&logNo=221054483327&proxyReferer=https:%2F%2Fwww.google.com%2F 리처드 파인만]〉, 《네이버블로그》, 2017-07-19 | *Soo , 〈[https://m.blog.naver.com/PostView.nhn?blogId=miseos&logNo=221054483327&proxyReferer=https:%2F%2Fwww.google.com%2F 리처드 파인만]〉, 《네이버블로그》, 2017-07-19 | ||
2020년 8월 20일 (목) 11:30 판
리처드 파인만(Richard Feynman)은 미국의 물리학자이다. 파인만 다이어그램이라 불리는 아원자 입자의 행동을 기술하는 시공간 다이어그램을 창안하였으며, 전자기장과 전자의 상호작용을 양자 역학적으로 설명하는 양자전기역학을 만들었다. 노벨물리학상을 받았으며, 아인슈타인 다음으로 인기있는 물리학자로 일컬어진다.
목차
생애
고등학교 이전
리처드 파인만은 1918년 5월 11일, 뉴욕시에 있는 퀸즈의 파 락어웨이(Far Rockaway)에서 태어났다. 파인만의 부모는 19세기 말에 미국으로 이주한 유대인 가정이지만, 유대교의 의식을 따르지는 않았다. 아버지인 멜빌 파인만은 아들에게 문제해결식 접근법을 교육시켰고, 권위를 수동적으로 받아들이지 말고 이를 의심할 것을 가르쳤다. 이러한 아버지의 교육방식은 어린 파인만이 옳은 답변보다는 질문을 통해 생각하는 습관을 기르게 되었고, "가장 높은 형식의 이해는 웃음과 인간적인 애정이다."라는 어머님의 교육을 통해 그가 평생동안 간직하게 되는 천성인 유머와 재치가 어디로부터 왔는지 알 수 있다. 파인만은 공립학교를 다니면서 화학 및 수학에 대해 우수한 성적을 받았으며, 라디오 수리에 많은 관심을 두었고, 기계를 다루는 데에 재능이 있었다. 그래서 10살부터 자신의 실험실에서 사용할 낡은 라디오를 모으기 시작했고, 12살에는 이웃의 라디오를 고치기도 했다.[1][2]
고등학교 시절
고등학교 시절에는 집 근처의 파 로커웨어(Far Rockaway) 고등학교에 다녔는데, 수학에서 두각을 드러내며 15살에 혼자서 삼각함수, 고급 대수학, 해석 기하학, 무한수열, 미적분학을 독학하였다. 그 당시에 뉴욕 대학교에서 열린 수학 경시대회에서 1등을 하였고, 심사위원들은 2등과 1등의 점수 차이가 너무나 커 놀랐다고 전해진다. 고등학교 교사인 베이더(Bader)로 부터 17세기 최고의 수학자인 페르마(Pierre de Fermat)를 접하게 되었고, 파인만은 그로부터 많은 영감을 받게 되었다.[1][2]
대학교 시절
파인만은 컬럼비아 대학교에 응시했으나, 유대인에 할당된 입학생 수가 적어 합격하지 못하였고, 그 대신에 MIT 대학교에 입학하였다. MIT 대학교에서 수학과로 입학했으나 이후에 전기공학으로 전공을 변경하였고, 1학년 말에 물리학으로 다시 변경하였다. 파인만이 대학을 졸업할 때쯤 대학과 대학원 과정을 완전히 익혔고, 분자에 관한 양자역학에 대한 논문을 "피지컬 리뷰(Physical Review)에 냈다. 1939년, 3년 만에 MIT를 졸업한 파인만은 "1939 윌리엄 로웰 퍼트넘 수학 경시대회(1939 William Lowell Putnam Mathematical Competition)"에서 우승하여 하버드 대학에 입학을 신청하기도 전에 이미 허가를 받은 상태였다. 하지만 이론 물리학을 공부하기 위해 아인슈타인이 있는 프린스턴 대학원으로 갔다. 여기서 프린스턴 대학교는 파인만의 영어와 역사 등의 점수가 매우 낮고, 유대인이었기 때문에 입학을 주저했었다고 전해진다.
- 프린스턴 대학원
그는 1942년에 박사 과정을 마치고 박사 학위를 받았다. 그의 박사 논문은 당시 프린스턴 대학교의 물리학자 휠러(John Archibald Wheeler)가 지도하였는데, 여기서 파인만은 시간을 왕복하며 이루어지는 전자기적 상호작용의 이론을 제창했다. 이런 전자기학에 대한 접근법은 파동이론에 근거한 맥스웰의 전자기 이론을 시간과 공간에 의해 만들어진 물질적 원거리 작용에 기초한 것으로 대체하였으며, 그 방법은 입자가 한 공간에서 다른 곳으로 갈 때 입자가 취할 수 있는 가능한 모든 경로를 계산한 것이었다. 그가 이 주제에 대하여 강의했을 때, 교실에는 아인슈타인, 볼프강 파울리 등 물리학의 대표주자들이 참석하였다. 그가 박사학위를 받은 나이는 23살에 불과하였으나, 이미 그 당시 대표적인 이론 물리학자로 거듭났다.[1][2]
맨해튼 프로젝트
파인만이 박사 학위를 연구하던 당시에, 세계 2차대전이 진행 중이었으며, 로버트 오펜하이머가 비밀리에 원자폭탄은 만드는 맨해튼 프로젝트의 지도자가 되었다. 그는 훌륭한 과학자들을 로스 앨러모스(Los Alamos)로 모집하기 시작하였다. 그러던 중 프린스턴 대학교의 물리학자인 로버트 윌슨이 파인만에게 원자탄 개발 계획에 참여하지 않겠냐는 제안하였고, 파인만은 이를 받아들여 이 프로젝트에 참여하게 되었다. 처음에는 아내인 알린 그린봄(Arline Greenbaum)의 병으로 인해 망설였는데, 이때 오펜하이머가 근처에 그녀를 돌봐줄 병원을 찾아주면서 1943년 3월, 파인만은 이 프로젝트에 참여하게 되었다. 파인만은 한스 베테(Hans Bethe)가 이끌던 이론 물리 팀에서 핵폭발의 에너지 생산량을 예측하는 공식을 만들던 팀의 최연소 리더를 맡았다. 이 시절 그는 보안 문서를 보관하는 금고를 여는 방법을 알아내어 동료들의 금고를 열어 자신의 재주를 보여주곤 했다. 또한, 파인만은 물리학자가 아닌 수학자로도 일을 하였는데, 그러면서 복잡하고 어려운 계산들을 해결했다. 별의 핵융합을 발견한 그의 상사 한스 베테는 토론을 좋아하여 주위에 누군가 없다면 파인만의 사무실로 와 이야기를 하였고, 곧 친한 친구로 발전했다. 파인만은 베테와 일을 함께 하면서 능력이 놀라운 정도로 향상되었고, 3차 미분 방정식을 개발하였으며, 이는 이차 미분 방정식 계산보다 정확했다. 이 공식은 그가 아래에서 설명할 QED를 다루기 위해 만들고 있는 방정식과 많이 비슷했으며, 핵폭탄을 만드는 마지막 단계 동안에 파인만은 존 폰 노이만에 의한 성공적인 플루토늄 폭탄을 조립하는 전산 작업을 감독하고 있었다. 1945년 7월, 첫 번째 원자폭탄 실험을 직접 목도하였고, 그의 회고에 따르면 그 당시에 보호 안경을 쓰지 않고 육안으로 목격한 유일한 사람이었다고 한다. 파인만은 원자 폭탄 실험을 성공적으로 치렀을 때 매우 기뻐했으나, 일본에 원자폭탄이 투하되고 전쟁이 끝나면서 원자폭탄의 치명적인 힘에 대해 우려하는 쪽으로 입장이 바뀌었다.[1][2]
아내의 죽음
파인만이 프린스턴 대학교에 재학 중일 때, 고등학교 시절부터 좋아한 첫사랑 알린 그린봄과 결혼했다. 그녀는 당시에 결핵을 앓고 있었고, 파인만은 그 이유 때문에 결혼을 반대하는 부모님을 설득해야 했다. 2차 세계대전 중 파인만이 프로젝트에 참가하고 있을 때, 오펜하이머가 구해준 병원에서 알린은 살고 있었다. 하지만, 그녀의 병세는 회복되지 못하였고, 프로젝트가 끝나기 전이 1945년 6월에 25살의 나이로 사망하였다. 프로젝트의 원자폭탄 실험을 불과 한 달 앞두고 일어난 일이었다. 아내가 사망하고, 원자폭탄이 일본에 투여되고, 다시 학계로 돌아온 뒤에, 파인만은 죽은 부인에게 편지를 썼다. 이 편지는 파인만이 사망할 때까지 봉해진 채로 남아있었는데, 편지의 마지막에 “추신. 이 편지를 부치지 않는 것을 용서해요. 나는 당신의 새 주소를 모릅니다”라고 쓴 구절은 유명하다.[1]
QED
2차 세계대전이 종료되고 파인만은 배테가 재직 중이던 코넬 대학교의 교수가 되었다. 1945년부터 1950년까지 있었는데, 1945년에는 아내가 사망하였다면, 그다음 해에는 아버지가 사망하며 파인만에게는 고통의 시간이 왔다. 그러면서 한동안 힘든 세월을 보낸 뒤에, 파인만은 다시 양자 전기역학(Quantum Electrodynamics, QED)이론을 지속적으로 연구하였다. 이 연구에는 근본적인 문제가 있었는데, 상대적인 맥락에서 디랙 방정식의 개념을 확대할 방법이 없었다는 것이다. 아인슈타인의 방정식에는 항상 양에너지를 갖지만, 디랙의 방정식에는 음에너지를 가지고 있다. 디랙은 반입자를 예측하였고, 1932년 미국의 물리학자 칼 앤더슨(Carl Anderson)은 우주선 샤워 연구 중 전자와 같은 질량을 가지는 양전하를 발견하였다. 1947년에 라비(Isidor Isaac Rabi)의 컬럼비아 대학교 실험실에서 일하던 램(Willis Eugene Lamb)은 QED에 큰 영향을 미칠 실험 연구를 시작했다. 그는 이례 없는 정밀도를 가진 분광기술을 이용하여, 마이크로파 빔을 오븐에서 커지는 뜨거운 수소가스에 비추었다. 램은 디랙의 이론에서 동일한 에너지를 가져야 한다고 예측된 수소의 두 상태의 미세 구조 레벨이 특정한 양 만큼 전이된 것을 발견했다. 이른바 램 전이(Lamb shift)가 발견된 것이다. 디랙 이론의 두 번째 결함은 그해에 같은 컬럼비아 대학 실험실에서 일하던 쿠시(Polykarp Kusch)에 의해 발견되었다. 이후 셸터 아일랜드 학회의 마지막 날에, 파인만은 양자 역학의 시공간 접근법에 관한 강의를 하였으며, 이후에 이러한 방법을 통해 QED의 난제들을 해결하기 위한 결정적인 시도들을 하였다. 셸터 아일랜드 학회 이후에, 여러 양자 분야 이론가들은 디랙의 이론에서 본질적으로 전자의 자기 상호작용(self-interaction)에 관한 개념이 빠져 있다는 것을 알게 되었고, 이 문제에 대한 슈윙거의 해법은 무한 에너지의 문제를 수학적으로 다룰 수 있는 재규격화의 방법을 도입하는 것이었다. 이 방법으로 램 전이가 설명되었다.
- 파인만 다이어그램
파인만은 그의 시공간 다이어그램을 1948년 한 학회에서 처음 발표하였고, 이를 통해 물질, 에너지, 진공에 관한 기본적인 개념이 변경되었다. 1949년, 파인만은 다이어그램의 완전한 버전에 대한 논문을 썼는데, 여기에서는 시공간에서 앞을 향해 움직이는 두 전자가 가상의 광자를 교환하며 상호작용하는 것을 보여주는 사다리와 같은 그림이 처음 등장했다. 1950년이 되면서 파인만의 상대적으로 단순한 도표는 슈윙거의 오퍼레이터 양자전기역학을 압도하기 시작했고, 다양한 논문들이 파인만을 인용하기 시작했다. 그는 1954년 알베르트 아인슈타인상 수상에 이어, 1965년 양자전기역학의 초기공식화에 대한 부정확성을 수정한 연구로 미국의 줄리언 슈윙거, 일본의 도모나가 신이치로와 함께 노벨 물리학상을 수상하였다. 특히 파인만이 고안한 파인만 다이어그램은 이후의 이론 물리학에 널리 이용되었다. 이런 업적으로 20세기 거시적 물리 세계의 대가가 아인슈타인이었다면 미시적 물리 세계의 대가는 파인만이라고 할 정도로, 아인슈타인 이후 최고의 천재 물리학자로 꼽히게 되었다.[1][2][3][4]
이후의 삶
1950년에 파인만은 캘리포니아 공과대학에서 이론 물리학 교수가 되었고, 1950년 초반에 절대온도 0도에서의 기괴하고 마찰이 없는 액체 헬륨의 움직임인 초유제의 특성에 양자 역학을 적용하는 연구를 진행하였다.
1958년에는 광자에 의한 고에너지 전자의 산란에 대해 스탠퍼드 선형 가속기에서 실험 물리학자와 함께 작업하는 동안, 그는 원자핵 내부의 가상의 단단한 입자인 패트론에 대한 이론을 개발하였고, 이는 쿼크에 대한 이론을 이끌어내는데 큰 도움을 주었다.
1986년 1월에는 7명의 승무원을 태운 우주왕복선 챌린저호가 폭발하여 승무원 전원이 사망하는 사건이 발생하였는데, 대통령의 명령에 의해 구성된 조사 위원회에서 파인만은 논리적 추론만으로 사고의 원인을 알아내었다. 사고의 원인이 오링(O-ring)이라는 부품에 있었음을 밝혀내었는데, 고체 로켓 부스터에 사용된 고무 재질인 오링이 추운 날씨로 인해 탄력을 잃으면서 고온 고압의 가스가 오링 사이로 누출되었고 그에 불이 붙으면서 폭발한 것이었다. 이 사건을 통해 파인만은 천재 물리학자라는 호칭이 헛된 것이 아님을 다시 한번 증명해내었다.[1][3][4]
주요 업적
- 중성자 성질에 대한 이론적 규명
- 양자 전기 역학의 재규격화를 이루어 내었고, 이로 인해 노벨물리학상을 수상하였다.
- 약한 상호작용의 V-A 상호작용 제안
- 경로적분 제안
- 원주율 소수 762~767 자리에서 9가 연속으로 6번 나옴을 발견해냄(파인만 포인트)[5]
파인만 다이어그램
리처드 파인만이 도입한 파인만 다이어그램은 양자장에서 입자들의 변화를 쉽게 표현해주는 그림이다. 양자장론에서 이 다이어그램을 통해 전이진폭 혹은 상관 함수의 계산에서 나타나는 항들을 나타내는 도형이며, 시공간 다이어그램이다. 하나의 물리적 과정은 아래에서 시작하여 위에서 또는 왼쪽에서 시작하여 오른쪽에서 끝난다. 다이어그램의 모든 선은 입자를 나타내는데, 세 가지 유형의 기본입자가 존재한다. 세 개의 선이 만나는 정점은 전자기의 상호작용을 의미한다.양자장론의 정준 수식화에서 파인만 다이어그램은 산란 행렬의 윅의 정리에 따른 섭동 이론적 전개에서의 특정 항을 나타낸다. 이때 전이진폭은 양자계의 시작과 끝 사이의 상태에 대한 산란 행렬의 성분이다. 경로 적분의 관점에서 보면, 전이진폭은 계의 처음과 마지막 상태 사이의 모든 가능한 경로들의 합이다. 파인만 다이어그램은 성분이 결합하고 쪼개어지는 그림을 통해 입자의 특정 경로를 직관적으로 나타낸다.
- 규칙
입자의 전파인지는 변이고, 입자 사이의 상호작용은 꼭짓점으로 나타낸다. 입자가 그 반입자와 다를 경우, 그 변은 유향(directed) 변이고, 화살표로 방향을 표시한다. 입자의 경우에는 초기 상태에서 최종 사태를 향하여 가리키고, 반입자는 최종 상태에서 초기 상태를 가리킨다. 입자가 그 반입자와 같은 경우에는 화살표로 표시하지 않으며, 광자와 W 및 Z 보손은 물결선으로 나타낸다. 글루온은 꼬인 선으로 나타내고, 기타 입자를 구별할 필요가 있다면 변 옆에 부호로 표현한다.[6][7][8]
QED
QED는 전자와 빛을 양자 현상으로 다룬다. 양자라는 개념은 20세기 들어서면서 나타났다. 그 당시에, QED는 과학자들에게 숙제와도 같은 것이었는데, 디랙과 슈뢰딩거가 방정식을 만들어내면서 성공하는 듯 싶었다. 하지만 무한대의 양이 출현 함으로써 문제가 발생하였고, 제2차 세계대전이 끝난 이후에 셸터 아일랜드 학회에서 과학자들이 모여 연구를 시작했다. 학회가 끝나고 슈윙거가 이 문제를 해결해내었지만, 그 과정이 너무나 복잡하고 어려워 다른 사람들이 이해하기에 어려움을 겪었다. 그런데 파인만은 슈윙거와는 다른 방식으로 이 문제에 대해 접근하였다. 그는 시공간의 한 점에서 다른 점으로 입자가 전파하는 방식으로 전자의 움직임을 파악하고자 했다. 여기서 파인만은 길적분이라는 아이디어를 도입하여 그 당시에 문제가 되었던 디랙 방정식과 슈뢰딩거 방정식의 충돌을 해결하였고, 이러한 방식은 기존의 슈윙거가 만든 방법보다 간단하고 빠르며, 눈에 보이는 방식으로 구할 수 있어 이해하기에 편리하였다.[9]
주요 저서
- 남이야 뭐라 하건
- 클래식 파인만
- 물리법칙의 특성
- 파인만의 물리학 강의
- 과학이란 무엇인가[10]
명언
- The first principle is that you must not fool yourself and you are the easiest person to fool. (첫째 원칙은 너는 너자신을 바보로 만들지 말아야만 하고 너는 바보가 되기 가장 쉬운 사람이라는 것이다.)
- I thought one should have the attitude of 'What do you care what other people think! (나는 누군가는 '다른 사람들이 어떻게 생각하는 니가 무슨 상관이니!'이라는 자세를 가져야만 한다.)
- If I could explain it to the average person, I wouldn't have been worth the Nobel Prize. (내가 평균적인 사람에게 그것을 설명할 수 있다면 나는 노벨상을 탈만한 가치가 없을 것이다.)
- I was born not knowing and have had only a little time to change that here and there. (나는 아무것도 모르고 태어났고 여기저기를 바꿀 정말 작은 시간만을 가졌다.)[11]
각주
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 홍성욱, 〈리처드 파인만〉, 《과학인물백과》
- ↑ 2.0 2.1 2.2 2.3 2.4 Soo , 〈리처드 파인만〉, 《네이버블로그》, 2017-07-19
- ↑ 3.0 3.1 최성우, 〈팔방미인 물리학자, 리처드 파인만〉, 《사이언스타임즈》, 2017-11-03
- ↑ 4.0 4.1 안종주, 〈<파인만의 물리학 강의>의 리처드 파인만〉, 2014
- ↑ 리처드 파인만 위키백과 - https://ko.wikipedia.org/wiki/%EB%A6%AC%EC%B2%98%EB%93%9C_%ED%8C%8C%EC%9D%B8%EB%A7%8C
- ↑ 파인만 도형 위키 백과 - https://ko.wikipedia.org/wiki/%ED%8C%8C%EC%9D%B8%EB%A7%8C_%EB%8F%84%ED%98%95
- ↑ soma0sd, 〈파인만 다이어그램 (파인만 도형)〉, 《네이버 블로그》, 2013-07-10
- ↑ 정계섭, 〈도형에 의한 추론 (Schematic Reasoning) : 통시적 사례 연구〉, 《덕성여대》, 2006-11
- ↑ 임채호, 〈QED가 완성되기까지의 역사와 의미〉, 2015-05
- ↑ 〈리처드 파인만〉, 《교보문고》
- ↑ whatx4, 〈리처드 파인만(Richard P. Feynman) 잠언, 명언, 인용 - 1〉, 《티스토리》, 2016-10-10
참고자료
- 리처드 파인만 위키백과 - https://ko.wikipedia.org/wiki/%EB%A6%AC%EC%B2%98%EB%93%9C_%ED%8C%8C%EC%9D%B8%EB%A7%8C
- 홍성욱, 〈리처드 파인만〉, 《과학인물백과》
- 〈리처드 파인만〉, 《교보문고》
- 안종주, 〈<파인만의 물리학 강의>의 리처드 파인만〉, 2014
- 임채호, 〈QED가 완성되기까지의 역사와 의미〉, 2015-05
- whatx4, 〈리처드 파인만(Richard P. Feynman) 잠언, 명언, 인용 - 1〉, 《티스토리》, 2016-10-10
- Soo , 〈리처드 파인만〉, 《네이버블로그》, 2017-07-19
- 최성우, 〈팔방미인 물리학자, 리처드 파인만〉, 《사이언스타임즈》, 2017-11-03
같이 보기
 이 문서는 사진 수정이 필요합니다.
이 문서는 사진 수정이 필요합니다.

 위키원
위키원