레인달

레인달

레인달(Rijndael)은 벨기에의 암호학자 존 대먼(Joan Daemen)과 빈센트 라이먼(Vincent Rijmen)에 의해 개발된 대칭키 암호 알고리즘이다. 미국 국립표준기술 연구소에서 진행한 차세대 암호 알고리즘 공모에서 마지막으로 선정되어 AES로 채택되었다. 따라서 레인달 알고리즘을 AES라고 부르기도 한다.

개요

1997년 1월 2일에, 미국 국립표준기술 연구소는 DES를 대체할 새로운 암호 기법의 필요성을 느꼈다. 따라서 3DES와 같거나 더 뛰어난 보안성을 갖고 개선된 암호 기법을 공모했는데, 공모에서 선정될 암호의 정식적인 이름은 1997년 9월 2일에 AES로 정해졌다. 총 세 차례의 대회는 1차에서 21개의 알고리즘이 제안되었고, 2차에서 15개의 알고리즘이 통과된 후, 3차에는 5개의 알고리즘만이 후보 알고리즘으로 남겨져 최후에는 하나만 남았다. 여기서 살아남아 AES로 선정된 알고리즘이 존 대먼과 빈센트 라이먼이 개발한 레인달 알고리즘이다. 따라서 AES는 레인달 알고리즘을 뜻한다.

레인달 알고리즘의 명칭은 존 대먼과 빈센트 라이먼의 이름에서 따온 것이다. 미국 국립표준기술 연구소에서 조건으로 내세운 다양한 방식의 공격에 대한 안전성을 갖추고 있으며, 속도 및 메모리 요구량과 알고리즘의 유연성, 단순성을 만족한다. 대칭형 암호 알고리즘 중에서도 블록 암호 알고리즘 방식이기 때문에 암호화 및 복호화 속도가 비대칭형 암호 알고리즘보다 빠르고, 암호화를 해도 크기가 증가하지 않아서 암호화 문의 크기가 평문보다 크지 않다는 장점을 갖고 있다. 128비트 평문으로 128비트 암호문을 출력하며, 논-파이스텔 알고리즘에 속한다. 암호화 키의 길이에 따라서 실행되는 라운드의 수 또한 다르며, 이들 각각은 10, 12, 14라운드를 실행한다. 암호화 키는 128, 192, 256 세 가지 중 하나가 될 수 있으며, 각각은 AES -128, AES -192, AES -256으로 불린다. 그러나 어떤 경우에서라도 키 확장 알고리즘으로부터 생성되는 라운드 키의 크기는 평문과 암호문의 크기와 같은 128비트다. S-box를 간단히 설명하자면, 입력 데이터를 지정된 숫자로 바꿔서 암호를 깨기 어렵게 만드는 기법이라고 할 수 있다. AES는 이를 새롭게 재발명하여, 만약 암호화 속도를 높이고 싶다면 S-box를 메모리에 넣어두고, 프로그램 메모리양을 줄이고 싶다면 S-box를 연산으로 구해내는 기법을 사용한다. 레인달 알고리즘은 크게 네 단계로 나뉜다. Add Round Key, Sub Byte, Shift Row, Mix Column이 반복되어 이루어지는 것이 특징이며, 각 라운드는 하나의 자리바꿈 연산과 세 개의 치환 연산으로 구성되어 있다.

1. 키 확장 : 키 스케줄이라고도 부른다. 128, 192, 256비트 길이인 하나의 주 암호화 키를 받아서 아래의 라운드 들에서 사용할 128비트 라운드 키를 여러 개 생성한다.
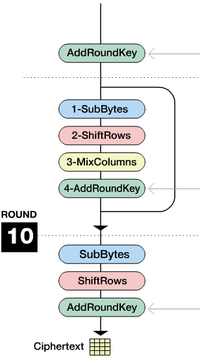
2. 0 라운드 : 위 단계에서 생성한 라운드 키 중 첫 번째 키를 사용하며, AddRoundKey키를 한 번 실행한다.
3. 1~(9, 11, 13) 라운드 : SubBytes, ShiftRows, MixColumns, AddRoundKey를 순서대로 실행한다. 이 과정을 AES-128, 192, 256에 따라 각각 9번, 11번, 13번씩 반복한다.
4. 마지막 10, 12, 14번째 라운드 : SubBytes, ShiftRows, AddRoundKey를 차례대로 실행한다.

배경

1997년 1월 2일 미국 국립표준기술 연구소는 DES를 대체할 새로운 암호 기법의 필요성을 느끼고, 보안성이 3DES와 비슷하거나 더 뛰어나게 개선된 암호 기법을 공모했다. 1997년 9월 2일, 공모에서 마지막으로 선정될 암호의 이름이 AES로 정해졌다. 미국 국립표준기술 연구소는 암호론의 케르코프 원리에 의하여 128비트 블록을 128 혹은 192 혹은 256비트 키 길이로 처리할 수 있고, 무료로 배포할 수 있어야 한다는 제한 조건이 있었다. 공모에서 제시한 평가 기준은 총 5가지로, 각각 보안, 메모리 요구량, 계산적 효율성, 하드웨어와 소프트웨어 면에서의 적합성, 유연성이었다. 1998년 1월 15일 마감일을 기준으로 하여 총 21개의 알고리즘이 제안되었으며, 이들 중에 단 15개의 알고리즘만이 AES 후보로 선정되어 안전성을 평가받았다. 1998년 8월 20일, 미국 국립표준기술 연구소는 선정된 15개의 암호 알고리즘에 대해 제1차 AES 후보 대회를 개최했다. 그리고 1999년 3월에 제2차 AES 후보 대회가 개최되었고, 1999년 8월에 총 5개의 후보 알고리즘만을 최종 후보로 선정하여 많은 암호학자로부터 안전성 평가를 받도록 하였다. 이 과정에서 남은 5개의 알고리즘의 이름은 MARS, RC6, 레인달, Serpent, Twofish이다. 2000년 4월에 제3차 AES후보 대회가 개최되고, 심사 끝에 2000년 10월 2일에 AES로 선정된 것이 존 대먼과 빈센트 라이먼이 개발한 레인달 알고리즘이다. 국 국립표준기술 연구소는 이에 뒤이어 2001년 2월 28일에 연방 정보 처리 표준으로서 AES를 공개 및 리뷰하고, 배포하면서 기밀성 있는 정보에 DES를 대체하여 AES를 사용하기 시작했다. 2001년 11월 16일에는 레인달 알고리즘, 즉 AES가 표준으로 채택되었으며, 2001년 12월 4일에는 FIPS 197로 등록되었다.

AES 선정 과정에서 주목해야 할 점은 개방성과 국제 흐름이 반영되었다는 것이다. 세 차례의 대회와 많은 사람의 의견을 수렴하여 공개하여 반영하였으며, 이 과정에서 전문가와 비전문가의 의견을 가리지 않고 받아들여 다양한 의견을 수집했다. 피드백의 기회를 부여하고 다 함께 이슈에 관해 토론하는 과정이 있었으며, 이 뿐만 아니라 다양한 분야 전문가들의 의견도 반영되었다. 수학자, 암호학자, 공학자, 컴퓨터학자 등 다양한 분야의 전문가들이 의견을 적극적으로 반영하고 뛰어난 성능을 갖춘 동시에 안전성도 개선된 알고리즘을 선택할 수 있었다. 국제화 측면에서 AES 선정 과정을 분석하면, 선정된 알고리즘들은 15개의 후보 알고리즘의 개발자들이 가진 다양한 국적만큼 다양한 국가의 평가를 받았다. 당시 알고리즘의 안전성 평가에 적극적으로 참여했던 국가들은 대한민국을 비롯하여 노르웨이, 독일, 미국, 벨기에, 영국, 이스라엘, 일본, 캐나다, 코스타리카, 프랑스, 호주가 있다.

제2차 AES 후보 대회는 이례적이게도 미국이 아니라 이탈리아 로마에서 개최되었다. 평가에서 AES 후보 알고리즘들은 다음과 같은 세 가지 조건을 만족해야 했다. 하나는 안전성으로, 후보 알고리즘들이 절대적으로 갖춰져야 하는 부분이었고, 특히 대칭 키 암호를 분석하는 대표적인 방법인 선형 공격과 차분 공격에 대한 안전성 증명이 주를 이루었다. 두 번째는 비용으로, 스마트카드, 하드웨어, 소프트웨어의 구현을 위한 다양한 형태의 계산 효율성을 참고하여 평가되었다. 여기서 계산 효율성이라고 하는 것은 속도 및 메모리 요구량 등을 의미한다. 세 번째는 알고리즘 및 구현 특성으로, 이 기준은 유연성과 알고리즘의 단순성에서 주로 평가하였다. 마지막 평가 과정에서 남았던 5개의 알고리즘 중에서 레인달 선정되고 나머지 4개의 알고리즘은 탈락했지만, 모두 안전성이 떨어지는 알고리즘은 절대 아니었다. 다만 레인달 알고리즘이 안전성과 속도, 효율성, 구현 및 유연성이 다른 후보 알고리즘들보다 우수했을 뿐이다.

특징

AES, 즉 레인달 알고리즘의 특징 중 하나는 파이스텔 구조가 아니라는 점이다. 전형적인 파이스텔 구조는 데이터 블록의 반쪽을 다른 반쪽을 수정하는 데 사용하고, 그 두 반쪽을 서로 교환한다. AES는 파이스텔 구조를 사용하지 않고 각 라운드에서 대체와 치환을 이용하여 데이터 블록의 전체를 병렬 처리한다. 또, 입력으로 사용하는 키를 44개의 32비트 워드 배열로 확장한다. 4개의 서로 다른 128비트 워드를 각 라운드에서 라운드 키로 사용한다. 다음의 네 가지 단계를 이용하는데, 치환 한 번과 대체 세 번이다.

• 바이트 대체 : S-box 표를 이용하여 바이트 단위 형태로 블록을 교환한다.
• 행 이동 : 단순히 행과 행을 치환한다.
• 열 섞기 : 열에 속한 모든 바이트를 순환 행렬을 이용하여 함수로 열에 있는 각 바이트를 대체해서 변형시킨다.
• 라운드 키 더하기 : 확장된 키의 일부와 현재 블록을 비트별로 XOR한다.

암호와 복호를 위하여 라운드 키 더하기 단계에서 시작하며, 각 라운드에서는 네 단계를 모두 포함하는 9라운드를 수행하고, 세 단계로 구성된 열 번째 라운드를 수행한다. 주의해야 할 점은 오직 라운드 키 더하기 단계에서만 키를 사용해야 한다는 것이다. 그래서 암호화와 복호화 과정의 시작과 끝은 항상 라운드 키 더하기 단계이다. 시작이나 끝에 수행되는 다른 단계들은 키 없이 역방향 계산이 가능하기 때문에, 보안을 강화하는 데는 별다른 역할을 하지 못한다. 라운드 키 더하기 단계는 그 자체는 강력하지 않으나, 세 단계와 같이 작동하여 비트를 뒤섞는 역할을 수행한다. 그러나 각각은 키를 사용하지 않기 때문에 보안성을 제공하는 것은 아니다. 이 암호 단계를 살펴보면 블록에 XOR 암호화를 하고, 그다음 블록을 뒤섞고, 그 뒤에 다시 XOR 암호화를 하는 것으로 이를 번갈아서 적용하는 것을 볼 수 있다. 이 구조는 효과적이고 보안성을 매우 강화한다.

각 단계를 역으로 계산하기는 쉽다. 바이트 대체, 행의 이동, 열 섞기 단계는 복호화 알고리즘에서 사용되는 역함수이다. 라운드 키 더하기 단계에서는 같은 라운드 키를 블록에 XOR 수행해서 역을 계산한다. 대부분의 블록 암호처럼 복호화 알고리즘에서는 확장 키를 순서를 뒤집어서 적용하는데, 복호화 알고리즘과 암호화 알고리즘이 동일한 것은 아니다. 이것이 바로 AES의 구조가 가지고 있는 특성이다. 네 단계가 모두 역계산이 가능하기 때문에 복호화를 하면 평문을 얻을 수 있는 것이 당연하다. 암호화와 복호화의 마지막 라운드는 세 단계로만 구성된다. 이러한 특성들은 AES 암호가 역으로 잘 작동되도록 하는 데 필요한 조치이다.

안전성

미국 정부에서 채택해서 정부의 기밀문서를 암호화한 알고리즘이다. 즉, 한 나라의 정부가 신용하는 알고리즘이다. 현재까지는 아직 AES보다 전반적으로 월등한 암호 알고리즘이 나오지 않았고, 현존하는 최강의 암호화 알고리즘이며, 키 없이 해독하는 것이 거의 불가능하다고 믿어지고 있다. 심지어 다른 최신 암호와 마찬가지로, 기지 평문 공격을 이용한 해킹 기술로도 해독이 불가능하다고 알려져 있다. 소수를 사용한 암호화의 특성을 이용한 공개키 암호화 방식 등이 양자 컴퓨터에 취약할 가능성을 보여주지만, SPN을 기반으로 하는 AES의 특성상으로는 상대적으로 양자컴퓨터에 안전하다. 시간이 지남에 따라 컴퓨팅 기술이 급속하게 발전하여, 현재 권장되는 암호화 수준은 192비트 이상이다. 대다수의 금융기관이나 웹사이트들은 256비트 이상의 암호화 체계로 전환했다.

주의할 점

레인달 알고리즘이 AES 공모에 출품작으로 참여했고, 그 결과 AES로 채택되었다. 하지만 그렇다고 해서 레인달과 AES의 개념이 완전히 동일한 것은 아니다. 흔히 AES와 레인달 알고리즘이 같은 개념이라고 생각하는 경우가 많지만, 엄밀히 말하면 AES은 알고리즘이 아니며 레인달은 대칭키 암호 알고리즘이다. 레인달이 블록 암호 알고리즘 방식이기 때문에 블록 운용방식과 블록 크기, 키를 통해서 평문을 암호화해야 한다. 만약 평문이 블록 크기의 배수가 되지 않는다면 암호화를 진행할 수 없기 때문에 이 때는 패딩 방식을 결정해서 문장의 길이를 배수가 되도록 맞춰주는 별도의 작업을 진행한다. 레인달은 가변 블록 크기, 가변키 길이 및 가변 라운드 수를 가진 블록 암호이며, 블록 길이와 키 길이는 128비트에서 256비트까지 32비트의 배수로 독립적으로 지정할 수 있다. 그러나 AES에 맞추어 변형된 레인달의 경우, 블록 크기는 128로 제한되고 키 길이는 128, 192, 256비트로만 제한된다. 레인달-256과 레인달-192는 AES, 즉 레인달-128과 완전히 다른 알고리즘으로 간주해야 한다. AES는 레인달 알고리즘의 일부분이다. 블록의 크기가 256비트인 AES는 없기 때문에, AES 모듈이라고 만들어진 모든 모듈은 블록의 크기가 128비트라고 가정하고 개발되었다.

레인달 알고리즘과 AES의 차이(단위:비트)

명칭	알고리즘인가?	블록의 크기	키 크기
레인달	O	128, 192, 256	128. 160, 192, 224, 256
AES	X	128(16 바이트)	128, 192, 256

알고리즘

각 라운드는 네 가지 단계를 반복한다. 각 단계는 Add Round Key, Shift Rows, Sub Bytes, Mix Column이다.

키 스케줄

키 확장이라고도 한다. 하나의 주 암호화 키에서 많은 라운드 키들을 생성해낸다. 주 키의 길이에 따라서 총 라운드 수도 달라지기 때문에, 만들어야 할 라운드 키의 개수도 다르다. AES-128, 192, 256에 따라서 각각 11개, 13개, 15개의 라운드 키를 생성한다. 레인달 알고리즘은 라운드 키를 생성할 때 32비트, 즉 4바이트 단위로 연속적으로 생성한다. 레인달 알고리즘은 블록의 크기를 허용하기 때문에 하나의 라운드 키는 이 4바이트 워드를 네 개 뭉쳐서 생성한다. 따라서 AES-128, 192, 256 버전은 각각 44, 52, 60개의 4바이트 워드를 생성해야 한다.

Add Round Key

데이터와 키를 XOR 연산한다. Add Round Key는 처음에 한 번 수행한 뒤에, 각 라운드에서 한 번씩 하여 총 (라운드+1)번 수행된다. 예를 들어 AES 128을 기준으로 하면 라운드는 10이고, 총 11번 수행된다. 상태 내의 각각의 바이트들과 라운드 키와의 비트 단위 EXOR 연산을 수행하기 때문에 역변환도 동일한 방식으로 연산한다. 레인달의 복호화 과정은 역변환된 함수들로 대체한 후에 암호화 순서를 그대로 수행한다.

Shift Rows

행 단위로 시프트 연산을 한다. 상태 내의값들을 변경시키지 않고 첫 번째 행을 제외한 나머지 행들만 왼쪽으로 이동시키는데, 각각 1, 2, 3바이트씩 순환 이동으로 위치를 바꾼다. 역 Shift Rows 변환의 경우에는 첫 번째 행을 제외한 나머지 행들을 Shift Rows의 반대 방향, 즉 오른쪽으로 각각 1, 2, 3바이트씩 순환 이동을 시켜 위치를 바꾼다.

Sub Bytes

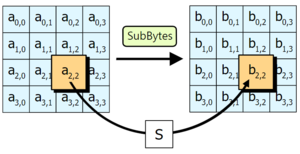
Sub bytes 연산은 바이트 단위로 치환을 수행한다. 8비트 단위로 데이터를 치환하는 연산으로서, 실제 연산은 1바이트를 갈로아필드상에서 역원을 구하고, 그 후에 아핀 변환을 하는 연산이다. 8비트씩의 연산을 반복해서 128비트 모두를 치환한다. 입력된 128비트 블록을 2차원 형태의 4x4로 구성된 상태로 변환해서, 상태 내의 각각의 바이트에 대해 치환 연산을 수행한다. 메모리가 여유 있는 경우라면 모든 입력에 대한 연산을 계산한 표인 S-box를 생성하고, 이를 이용하여 치환하는 방법도 많이 사용한다. Sub Bytes 변환은 2단계 동작으로 이루어지는데, 첫 번째는 유한체 상에서 입력된 상태 내의 각각의 바이트 값들에 대해서 곱셈의 역원을 구하고, 두 번째로 구한 바이트 값들에 유한체 상에서 변환을 수행한다. 역 Sub Bytes 변환은 앞의 변환을 역으로 수행하고 곱셈의 역원을 구한다.

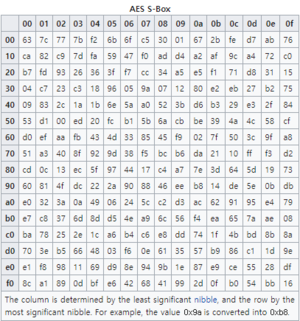
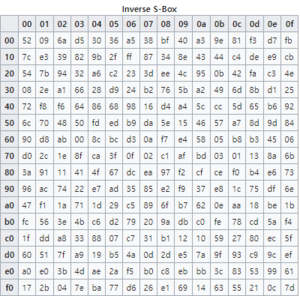
다음은 레인달 Sub Bytes S-box와 인버스 S-box, 즉 역방향 S-box이다. 레인달 알고리즘의 역방향 S-box는 Sub Bytes와 흡사하지만, 복호화할 때의 단계이다. 레인달의 S-box는 특별히 선형 및 차등 암호 해석에 내성을 갖도록 설계되어 있다. 이는 입력 및 출력 비트의 선형 변환 사이의 상관관계를 최소화하고 그와 동시에 전파 확률을 최소화함으로써 수행된다. 또, 레인달의 S-box는 정적 S-box를 이용하는 암호에 내장된 백도어의 의심을 물리치는 레인달 암호로 대체될 수 있다. 저자들은 "평균" 상관관계 및 차이의 전파 특성을 가진 S-box를 사용할 때는 레인달 암호 구조가 차등 및 선형 암호 해석에 대해서 충분한 저항을 제공해야 한다고 주장한다.

Mix Column

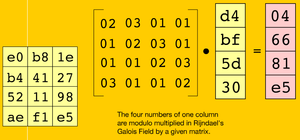
각각 바이트에 특정 행렬과 column 별로 곱 연산을 진행한다. 여기서 곱연산은 xtime을 이용하여 구현하며, 덧셈은 XOR 연산으로 수행한다. x2연산의 경우에 xtime이라고 불리는데, 왼쪽으로 1비트 시프트 한다. 연산하는 값의 최상위 비트가 1인 경우에는 0x1b를 XOR한다. 이는 2진수에서 왼쪽 시프트 연산을 하면 x2가 되고, 기약 다항식의 최상위 비트를 제외하고 표현한다면 0x1b이기 때문이다. 곱셈 연산이 미리 진행되는 행렬의 경우에는 미리 정의된 상숫값을 이용하는데, 여기서 오른쪽 연산하는 값은 각 column의 데이터 값이다. 예를 들어 첨부된 그림을 보면, $2*d4+3*bf+5d+30$이 된다. 각각을 계산하면, $2*d4\rightarrow d4<<$ 1^1b = b3, $3*bf=2*bf+bf\rightarrow bf<<$ 1^bf^1b = da 이 되므로 b3^da^5d^30 = 04가 나오게 된다. Mix Column 과정은 순열(Permutation) 과정이라고도 부른다.

참고자료

• 고급 암호화 표준 위키백과 - https://ko.wikipedia.org/wiki/%EA%B3%A0%EA%B8%89_%EC%95%94%ED%98%B8%ED%99%94_%ED%91%9C%EC%A4%80
• AES 나무위키 - https://namu.wiki/w/AES
• 신성호, 이재흥, 〈AES-128 Rijndael 암·복호 알고리듬의 하드웨어 구현〉, 《국가과학기술정보센터》, 2004
• thenine, 〈AES와 Rijndael〉, 《이글루스》, 2008-05-22
• Moserware, 〈A Stick Figure Guide to the Advanced Encryption Standard (AES)〉, 《디스커스》, 2009-11-22
• g0lem, 〈Rijndael과 AES의 차이점〉, 《it-swarm.dev》, 2013-05-09
• 워넝, 〈Rijndael(라인달)과 AES 암호화는 같다?〉, 《네이버블로그》, 2017-10-24
• jhh0712, 〈AES 암호〉, 《네이버블로그》, 2018-12-22
• 와이준Nye, 〈(암호학) 대칭키 암호 - AES(Advanced Encrytion Standard)〉, 《티스토리》, 2019-11-15

같이 보기

• 암호
• 암호 알고리즘
• 대칭키 암호 알고리즘
• AES

이 레인달 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반