"이퀴해시"의 두 판 사이의 차이
잔글 (→참고자료) |
잔글 (→생일문제) |
||
| 48번째 줄: | 48번째 줄: | ||
생일이 같은 두 사람을 찾는 것과 비슷하게, 암호학적 해시 결과가 같은(해시 충돌) 두 입력값을 찾는 것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시 충돌을 찾을 수 있다. 이러한 암호 공격을 생일 공격(birthday attack)이라고 부른다. | 생일이 같은 두 사람을 찾는 것과 비슷하게, 암호학적 해시 결과가 같은(해시 충돌) 두 입력값을 찾는 것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시 충돌을 찾을 수 있다. 이러한 암호 공격을 생일 공격(birthday attack)이라고 부른다. | ||
| + | |||
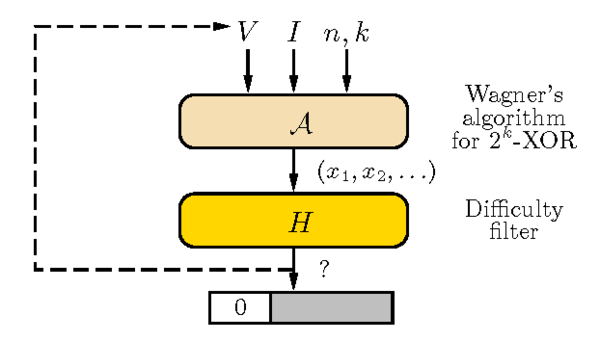
| + | 미국 캘리포니아 대학 버클리 캠퍼스( University of California, Berkeley ) 데이비드 바그너(David A. Wagner)는 생일문제를 더 일반화하여 다중 차원형의 k차원을 제시하였다. “n-bit 값의 k 리스트가 주어진 경우, 각 리스트에서 하나의 요소(element)를 찾아 k값의 배타적 논리합이 0 이되게 한다” 바그너는 이의 복잡도를 증명하고 이를 적용한 알고리즘을 만들어냈다. 여기서 시간과 공간의 규제는 엄격하였다. 일반화된 생일문제는 암호와 해시충돌의 연구에 상당히 중요하며 이의 특징은 작업증명 이론에 적합하다. | ||
| + | [[파일:k차원.png|섬네일|600픽셀|가운데|k차원]] | ||
==적용암호화폐== | ==적용암호화폐== | ||
2019년 5월 23일 (목) 14:30 판
이퀴해시(Equihash)는 작업증명에 사용되는 채굴알고리즘(Proof-of-Work mining algorithm)이다.
개요
룩셈브르그대학 정보통신기술 학제연구센터(the University of Luxembourg's Interdisciplinary Centre for Security, Reliability and Trust (SnT))[1]는 미국 샌디에이고에서 개최된 2016년 네트워크 & 분산시스템의 보안관련 학술토론회의에서 Memory-Hard Proof-of-Work 라는 알고리즘을 소개하였다. 이 알고리즘은 해시값을 찾아내기 위한 생일문제(Birthday problem)의 연구결과를 기반으로 엄격한 시간-공간의 균형을 규제하면서 또 병행으로 발생하는 예기치 못한 약간의 최적화를 허용하며 주문개발 ASIC의 원가-실적 균형 약화를 목표로 병행 추진이 메모리 대역폭에 병목처럼 제한되게 설계되었다. 이 알고리즘이 바로 이퀴해시(Equihash)이다. 이퀴해시는 시중에 출시 된 하드웨어가 비교적 넓은 메모리 대역폭을 보유하고 있는 가정하에 하드웨어 개선을 목적으로 주문제작을 추진하는데 투입하는 개발비용이 효과적이지 못하게 ASIC를 저애하는 특징이 있다.
이퀴해시는 룩셈브르그 대학 연구클럽 크립토LUX 암호학가 알렉스 비류코프(Alex Biryukov)와 Evernym, Inc.,의 암호연구원 드미트리 호브라토비치(Dmitry Khovratovich)가 2006년에 공동으로 발명하였다.
블록체인기반의 암호화폐 지캐시(ZCash), 아이온(Aion)이 보안, 프라리버시, ASIC 방식의 채굴 제어 등을 종합적으로 검토하여 이퀴해시를 자체 암호화폐 시스템에 적용하였다.[2]
발명배경
암호화폐 채굴상황 - 현재 비트코인 혹은 유사한 암호화페들의 채굴작업증명상황을 살펴보면 ASIC와 같은 채굴전용 하드웨어 출시로 인해 블록체인 시스템이 중앙화 상태로 가는 추세가 보인다.
채굴전용 하드웨어는 특정의 용도로 주문설계 제작된 하드웨어로서 작업증명을 진행하는 컴퓨팅과정에 월등한 성능을 나타내며 시중에 출시된 상용컴퓨터 대비 막강한 경쟁우세를 가지고 있다. 따라서 암호화페 채굴은 나날이 ASIC 하드웨어를 많이 보유한 세력들 또는 대규모의 암호화폐 마이닝풀로 중앙화 되어가고 있다.
사례를 들면 ASIC 하드웨어 제작사인 비트메인은 비트코인 네트워크 해시속도 51%의 연산력에 접근하는 해시속도를 보유하고 있다.
만약 비트메인의 보유해시속도가 51%에 도달하거나 초과하면 소위 말하는 51%공격이 이루어질 수 있는 가능성이 형성되며 트랜잭션이 반대로 이루어지거나 이중지불이 이루어지는 것을 포함한 네트워크의 붕괴를 일으킬 수 있다.[3]
연구과제 - 상기 암호화폐 채굴상황에 비추어 어떻게 하면 알고리즘의 방식으로 특정 용도의 목적으로 개발 한 하드웨어의 우세를 말소시켜 중앙화추세를 방지하냐는 컴퓨터과학에서 해결해야 할 과제이다. 이 과제를 해결하는 방식에는 시간원가제약, 공간원가제약, 시간-공간 균형 제약의 방식들을 활용하여 특정용도로 주문제작한 하드웨어의 경제성을 약화시키는 방식이 포함 된다.[4]
이퀴해시 - 상용컴퓨터와 주문제작 컴퓨터간의 채굴경쟁력 차이를 해소하고 간단한 작업증명 검증을 목표로 Memory-Hard방식의 해결방안을 모색한다. 주지하다싶이 알고리즘은 이의 시간복잡도와 공간복잡도로 측정을 할 수 있다.[3]
기본원리
특징
Progress-free process
- 중앙화된 채굴방식을 피면하고 스토캐스틱 프로세스(stochastic process)의 상태에서 기존 사건과 관계없이 임의의 주어진 시간에 채굴방식의 작업증명을 추진할 수 있다.
높은 AT원가(Large AT cost)
- 요청하는 작업증명의 컴퓨팅이 메모리집약으로 최적화된 ASIC 칩이 메모리영역에서 원가경쟁력이 안 나온다. 여기서 AT는 영역과 시간의 곱한 값을 표시한다.
작은 검증프로그램 크기와 인스턴트 검증(Small proof size and instant verification)
- 작은 검증 프로그램 크기로 최소의 메모리 사용량 상태에서 신속하고 충분하게 검증을 수행할 수 있다.
스팁 시간-공간의 균형(Steep time-space tradeoffs)
- Memory requirements imposed by the Equihash algorithm are worthwhile as long as attempts to optimize for memory disproportionately penalizes the user
유연성(Flexibility)
- 알고리즘의 개선과 아키택처의 변동을 감안하여 시간, 메모리, PoW의 steepness가 독립적으로 조율이 가능하게 하였으며 따라서 일정한 채굴율을 유지한다
제약받는 병렬성(Parallelism-constrained)
- 시스템적으로 병목(bottleneck)을 설치하여 병렬작업증명이 제약을 받게 한다
필요없는 최적화(Optimization-free)
- 총명한 증명자가 다른 사람을 초과하여 우세를 가지지 않도록 오늘날까지의 최적 알고리즘을 적용하였으며 가능한 최적화를 전부 검증
생일문제
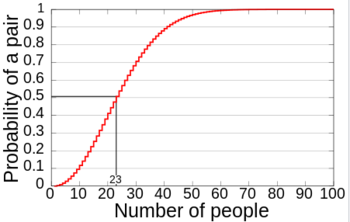
생일 문제(The generalized birthday problem)는 사람이 임의로 모였을 때 그 중에 생일이 같은 두 명이 존재할 확률을 구하는 문제이다.
생일의 가능한 가짓수는 365개(2월 29일을 고려할 경우 366개)이므로 366명 이상의 사람이 모인다면 비둘기집 원리에 따라 생일이 같은 두 명이 반드시 존재하며, 23명 이상이 모인다면 그 중 두 명이 생일이 같은 확률은 1/2를 넘는다.
생일 문제는 일반적인 인간의 직관과 다른 결과를 가지는 것으로 알려져 있다. 얼핏 생각하기에는 생일이 365가지이므로 임의의 두 사람의 생일이 같을 확률은 1/365이고, 따라서 365명쯤은 모여야 생일이 같은 경우가 있을 것이라고 생각하기 쉽다. 그러나 실제로는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50%를 넘고, 57명이 모이면 99%를 넘어간다.
생일이 같은 두 사람을 찾는 것과 비슷하게, 암호학적 해시 결과가 같은(해시 충돌) 두 입력값을 찾는 것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시 충돌을 찾을 수 있다. 이러한 암호 공격을 생일 공격(birthday attack)이라고 부른다.
미국 캘리포니아 대학 버클리 캠퍼스( University of California, Berkeley ) 데이비드 바그너(David A. Wagner)는 생일문제를 더 일반화하여 다중 차원형의 k차원을 제시하였다. “n-bit 값의 k 리스트가 주어진 경우, 각 리스트에서 하나의 요소(element)를 찾아 k값의 배타적 논리합이 0 이되게 한다” 바그너는 이의 복잡도를 증명하고 이를 적용한 알고리즘을 만들어냈다. 여기서 시간과 공간의 규제는 엄격하였다. 일반화된 생일문제는 암호와 해시충돌의 연구에 상당히 중요하며 이의 특징은 작업증명 이론에 적합하다.
적용암호화폐
채굴
각주
- ↑ "SnT", uni.lu
- ↑ "Equihash", Wikipedia
- ↑ 3.0 3.1 "Equihash Algorithm Explained", Mycryptopedia
- ↑ EtherDream, 〈怎样的 Hash 算法能对抗硬件破解〉, 《博客园》, 2017-02-22
참고자료
- "Zcash (ZEC)-Whitepaper", Whitepaper Database
- "Equihash", Wikipedia
- "Birthday problem", Wikipedia
- "Equihash - Mining Algorithms, Coins, Tokens", BitcoinWiki
- "What is Equihash? | Guide to Equihash Coins", UNHASHED
- 〈生日悖论〉, 《百度百科》
- "How the Equihash Algorithm Could Democratize Zcash Mining", Nasdaq.com
- Beam Privacy, "Speaking of Equihash", Medium, 2018-11-15
- "www.hashcash.org/papers/dagger.html", Hashcash
- EtherDream, 〈怎样的 Hash 算法能对抗硬件破解〉, 《博客园》,2017-02-22
- 최혜빈 기자, 〈中 비트메인, 이퀴해시(Equihash) 전용 채굴기 출시〉, 《코인리더스》, 2018-05-04
- Alexander Peslyak, "An analysis of Zcash's use of the Equihash proof-of-work scheme", Openwall, 2016-11-18
- David Wagner, "A Generalized Birthday Problem", Semantic Scholar
- Alex Biryukov/Dmitry Khovratovich, "Equihash: Asymmetric Proof-of-Work Based on the Generalized Birthday Problem", orbilu.uni.lu
- 〈계산복잡도이론〉, 《네이버지식백과》
- 雷盈 , 〈Zcash挖矿算法深度解析〉, 《巴比特》, 2016-11-25
- "David A. Wagner", Wikipedia
같이보기
| ||||||||||||||||||||||||||||||||||

 위키원
위키원