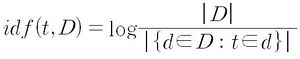"TF-IDF"의 두 판 사이의 차이
| (사용자 2명의 중간 판 11개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | TF-IDF | + | '''TF-IDF'''는 "Term Frequency-Inverse Document Frequency"의 약자로서, 단어가 문서에서 얼마나 중요한지를 반영하기 위한 숫자 통계이다. 오늘날 가장 인기 있는 용어 가중법 중 하나이며, 디지털 도서관의 텍스트 기반 권장 시스템의 83%가 이 방식을 사용하고 키워드 검색을 기반으로 하는 [[검색엔진]]도 이 방식을 사용한다. TF-IDF 검색을 사용하는 대표적인 알고리즘으로 [[BM25]]가 있다. |
== 개념 == | == 개념 == | ||
| − | TF-IDF 방식(Term Frequency-Inverse Document Frequency)은 정보 검색 및 텍스트 마이닝, 사용자 모델링 등에서 이용하는 가중치이며, 여러 단어로 이루어진 문서가 있을 때 포함된 특정 단어가 특정 문서 내에서 얼마나 중요한 지 단어와 문서의 연관성을 나타내는 통계적인 수치이다. 즉 발생 빈도는 적어도 중요한 항목에 가중치를 주기 위해 사용한다. | + | TF-IDF 방식(Term Frequency-Inverse Document Frequency)은 정보 검색 및 [[텍스트 마이닝]], [[사용자 모델링]] 등에서 이용하는 가중치이며, 여러 단어로 이루어진 문서가 있을 때 포함된 특정 단어가 특정 문서 내에서 얼마나 중요한 지 단어와 문서의 연관성을 나타내는 통계적인 수치이다. 즉 발생 빈도는 적어도 중요한 항목에 가중치를 주기 위해 사용한다. |
| − | + | ||
| − | TF-IDF의 값은 문서 내 단어의 빈도가 높거나 전체 문서 중 특정 단어를 포함한 문서가 적을수록 높다. 예를 들어 | + | [[TF]] 또는 '''용어빈도'''<!--용어 빈도-->는 단어의 빈도(Term Frequency)의 약자로 특정 단어가 문서에 나오는 빈도 수를 알 수 있다는 뜻이다. [[IDF]]는 특정 용어가 여러 문서에서 얼마나 자주 출현하는지를 나타내는 지표로서, '''역문서빈도'''<!--역문서 빈도-->라는 뜻이다. IDF는 DF의 반대(Inverse)라는 뜻인데, 여기서 DF는 Document Frequency의 약자로서 문서빈도, 즉 전체 문서 중에서 특정 단어를 포함하는 문서의 빈도를 의미한다. 그래서 IDF를 "역문서 빈도"라고 부른다. 결론적으로, 단어의 빈도를 의미하는 TF와 역문서 빈도를 의미하는 IDF라는 두 값을 곱한 것이 TF-IDF이다. |
| + | |||
| + | TF-IDF의 값은 문서 내 단어의 빈도가 높거나 전체 문서 중 특정 단어를 포함한 문서가 적을수록 높다. 예를 들어 ‘[[TP]]’라는 단어가 일반적인 문서들 사이에서 잘 나오지 않으므로, IDF 값은 높아지게 되고 문서의 핵심 단어가 될 수 있다. 하지만 ‘TPS’에 대한 문서를 모아둘 경우 이 단어는 상투어가 되기 때문에, 각 문서들을 세분화하고 구분할 수 있는 다른 단어들이 높은 가중치를 얻게 된다. TF-IDF 방식은 문서의 핵심어 추출, 검색 엔진 내 검색 결과 순위의 결정, 문서들 사이의 유사성 측정 및 분류 등의 용도로 사용되고 있다. 그뿐 아니라 다른 알고리즘과의 결합과 변형을 통해 특정 상품에 대한 평이 과도하게 부정적 또는 긍정적인 문서를 분류해 편향적인 리뷰 등을 걸러낼 수 있는 시스템을 만들 수도 있다. | ||
== 역사 == | == 역사 == | ||
| − | TF는 정보 검색의 아버지로 불리는 IBM 연구원 한스 피터 룬(Hans Peter Luhn, 1896~1964)이 1957년에 제시한 이론이다. 그는 1950년대 정보 검색 프로세스 및 자동 초록 작성 방법에 관심이 많았다. 그는 늘어만가는 문서들을 일일이 코딩하는 대신에 기계로 대체할 수 있는 방법을 찾고 있었다. 그때 그는 중요한 단어와 아이디어가 특정 문서에 등장하는 빈도가 더 높다는 전제를 발견했다. 그래서 처음에는 문서를 인덱싱(Indexing)하는 작업에 이 명제를 적용했다. 그 후 그는 자동 초록 작성(Abstracting) 기술에도 적용했다. 빈발하는 단어들에 우선 순위를 적용함으로써 정보 검색의 효율성을 높였으며 초록 작성에도 도움을 얻기 위한 목적이었다. 그의 명제는 IDF와 만나면서 완성체의 개념이 되었다. | + | TF는 정보 검색의 아버지로 불리는 IBM 연구원 [[한스 피터 룬]](Hans Peter Luhn, 1896~1964)이 1957년에 제시한 이론이다. 그는 1950년대 정보 검색 프로세스 및 자동 초록 작성 방법에 관심이 많았다. 그는 늘어만가는 문서들을 일일이 코딩하는 대신에 기계로 대체할 수 있는 방법을 찾고 있었다. 그때 그는 중요한 단어와 아이디어가 특정 문서에 등장하는 빈도가 더 높다는 전제를 발견했다. 그래서 처음에는 문서를 [[인덱싱]](Indexing)하는 작업에 이 명제를 적용했다. 그 후 그는 [[자동 초록 작성]](Abstracting) 기술에도 적용했다. 빈발하는 단어들에 우선 순위를 적용함으로써 정보 검색의 효율성을 높였으며 초록 작성에도 도움을 얻기 위한 목적이었다. 그의 명제는 IDF와 만나면서 완성체의 개념이 되었다. |
== 수학적 설명 == | == 수학적 설명 == | ||
| − | + | 앞서 언급했듯이, TF-IDF는 단어 빈도와 역문서 빈도를 곱한 값이다. 단어 빈도와 역문서 빈도의 값을 산출하는 방식은 여러 가지가 있다. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 우선 단어 빈도 tf(t,d) 값을 산출하기 위해 총 빈도, [[불린]](Boolean) 빈도, 로그(Logarithm) 스케일 빈도, 증가 빈도를 사용하는 방법이 있다. | ||
| + | ① 총 빈도는 가장 대중적인 방법으로 단순히 문서 내에서 나타나는 특정 단어의 총 빈도수를 사용하는 방법이다. 문서 d 내에서 단어 t의 총 빈도를 f(t,d)라고 할 때, 이 산출 방식은 tf(t,d) = f(t,d)로 표현한다. | ||
| + | ② 불린 빈도는 tf(t,d) = t가 d에 한 번 이상 나타나면 1, 아니면 0이다. | ||
| + | ③ 로그 스케일 빈도는 tf(t,d) = log (f(t,d) + 1)의 식을 사용한다. | ||
| + | ④ 증가 빈도는 가장 빈도가 높은 단어를 분모로 target 단어의 TF를 나눈 값이며, 문서의 길이가 상대적으로 길어질 경우 단어의 빈도 값을 조절하기 위해 사용된다. | ||
| + | [[파일:tf(t,d)2.JPG|썸네일|300픽셀|왼쪽]] | ||
| + | 그리고 역문서 빈도 idf(t,d) 값은 한 단어가 문서 집합의 전체에서 얼마나 공통적으로 나타나는지를 나타내는 값이며, 전체 문서 수를 특정 단어를 포함한 문서의 수로 나눈 후 로그를 취하여 얻을 수 있다. | ||
| + | [[파일:idf(t,D).JPG|썸네일|300픽셀|왼쪽]] | ||
| + | 이때, [[파일:D.JPG|썸네일|300픽셀|]]는 문서 집합 D의 크기 또는 전체 문서의 수를 의미하며, [[파일:dDtd.JPG|썸네일|300픽셀|]]는 단어 t가 포함된 문서의 수를 의미하므로 tf(t,d)는 0이 아니다. 단어가 전체 말뭉치 안에 존재하지 않을 경우 분모가 0이 된다. 이를 방지하기 위해 [[파일:1dDtd.JPG|썸네일|300픽셀|]]로 써야하지만, 생략하고 계산할 수 있다. | ||
| + | 결과적으로 TF-IDF 방식의 표기는 다음과 같다. | ||
| + | [[파일:tfidf(t,d,D).JPG|썸네일|300픽셀|왼쪽]] | ||
| + | TF-IDF의 값을 이용하면 모든 문서에 흔하게 나타나는 단어를 걸러낼 수 있다. IDF의 로그 함수값은 항상 1 이상이므로 IDF와 TF-IDF값은 항상 0 이상이다. 특정 단어를 포함하는 문서들이 많을수록 로그 함수 내 값이 1에 가까워지고, IDF와 TF-IDF값은 0에 가까워진다. | ||
=== 예시 === | === 예시 === | ||
| − | [[파일:TF-IDF예시.JPG|썸네일|700픽셀| | + | [[파일:TF-IDF예시.JPG|썸네일|700픽셀|오른쪽]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
D2 문서의 Not만 log2로 값이 나오게 된다. 즉 Not이라는 특정 단어가 D2 문서와 관계가 높다는 사실을 알 수 있다. | D2 문서의 Not만 log2로 값이 나오게 된다. 즉 Not이라는 특정 단어가 D2 문서와 관계가 높다는 사실을 알 수 있다. | ||
| 118번째 줄: | 45번째 줄: | ||
* Rachy, 〈[https://blog.naver.com/happyrachy/221285427229 텍스트 분석 방법(BOW, Word2Vec, TF-IDF)]〉, 《네이버 블로그》, 2018-05-27 | * Rachy, 〈[https://blog.naver.com/happyrachy/221285427229 텍스트 분석 방법(BOW, Word2Vec, TF-IDF)]〉, 《네이버 블로그》, 2018-05-27 | ||
* 이성규 기자, 〈[https://www.bloter.net/archives/264262 (블로터10th) 언론사가 알아야 할 알고리즘③ TF-IDF]〉, 《블로터》, 2016-09-28 | * 이성규 기자, 〈[https://www.bloter.net/archives/264262 (블로터10th) 언론사가 알아야 할 알고리즘③ TF-IDF]〉, 《블로터》, 2016-09-28 | ||
| + | |||
| + | == 같이 보기 == | ||
| + | * [[용어빈도]](TF) | ||
| + | * [[역문서빈도]](IDF) | ||
| + | * [[BM25]] | ||
| + | * [[추천 알고리즘]] | ||
| + | |||
| + | {{알고리즘|검토 필요}} | ||
2024년 10월 20일 (일) 12:41 기준 최신판
TF-IDF는 "Term Frequency-Inverse Document Frequency"의 약자로서, 단어가 문서에서 얼마나 중요한지를 반영하기 위한 숫자 통계이다. 오늘날 가장 인기 있는 용어 가중법 중 하나이며, 디지털 도서관의 텍스트 기반 권장 시스템의 83%가 이 방식을 사용하고 키워드 검색을 기반으로 하는 검색엔진도 이 방식을 사용한다. TF-IDF 검색을 사용하는 대표적인 알고리즘으로 BM25가 있다.
개념[편집]
TF-IDF 방식(Term Frequency-Inverse Document Frequency)은 정보 검색 및 텍스트 마이닝, 사용자 모델링 등에서 이용하는 가중치이며, 여러 단어로 이루어진 문서가 있을 때 포함된 특정 단어가 특정 문서 내에서 얼마나 중요한 지 단어와 문서의 연관성을 나타내는 통계적인 수치이다. 즉 발생 빈도는 적어도 중요한 항목에 가중치를 주기 위해 사용한다.
TF 또는 용어빈도는 단어의 빈도(Term Frequency)의 약자로 특정 단어가 문서에 나오는 빈도 수를 알 수 있다는 뜻이다. IDF는 특정 용어가 여러 문서에서 얼마나 자주 출현하는지를 나타내는 지표로서, 역문서빈도라는 뜻이다. IDF는 DF의 반대(Inverse)라는 뜻인데, 여기서 DF는 Document Frequency의 약자로서 문서빈도, 즉 전체 문서 중에서 특정 단어를 포함하는 문서의 빈도를 의미한다. 그래서 IDF를 "역문서 빈도"라고 부른다. 결론적으로, 단어의 빈도를 의미하는 TF와 역문서 빈도를 의미하는 IDF라는 두 값을 곱한 것이 TF-IDF이다.
TF-IDF의 값은 문서 내 단어의 빈도가 높거나 전체 문서 중 특정 단어를 포함한 문서가 적을수록 높다. 예를 들어 ‘TP’라는 단어가 일반적인 문서들 사이에서 잘 나오지 않으므로, IDF 값은 높아지게 되고 문서의 핵심 단어가 될 수 있다. 하지만 ‘TPS’에 대한 문서를 모아둘 경우 이 단어는 상투어가 되기 때문에, 각 문서들을 세분화하고 구분할 수 있는 다른 단어들이 높은 가중치를 얻게 된다. TF-IDF 방식은 문서의 핵심어 추출, 검색 엔진 내 검색 결과 순위의 결정, 문서들 사이의 유사성 측정 및 분류 등의 용도로 사용되고 있다. 그뿐 아니라 다른 알고리즘과의 결합과 변형을 통해 특정 상품에 대한 평이 과도하게 부정적 또는 긍정적인 문서를 분류해 편향적인 리뷰 등을 걸러낼 수 있는 시스템을 만들 수도 있다.
역사[편집]
TF는 정보 검색의 아버지로 불리는 IBM 연구원 한스 피터 룬(Hans Peter Luhn, 1896~1964)이 1957년에 제시한 이론이다. 그는 1950년대 정보 검색 프로세스 및 자동 초록 작성 방법에 관심이 많았다. 그는 늘어만가는 문서들을 일일이 코딩하는 대신에 기계로 대체할 수 있는 방법을 찾고 있었다. 그때 그는 중요한 단어와 아이디어가 특정 문서에 등장하는 빈도가 더 높다는 전제를 발견했다. 그래서 처음에는 문서를 인덱싱(Indexing)하는 작업에 이 명제를 적용했다. 그 후 그는 자동 초록 작성(Abstracting) 기술에도 적용했다. 빈발하는 단어들에 우선 순위를 적용함으로써 정보 검색의 효율성을 높였으며 초록 작성에도 도움을 얻기 위한 목적이었다. 그의 명제는 IDF와 만나면서 완성체의 개념이 되었다.
수학적 설명[편집]
앞서 언급했듯이, TF-IDF는 단어 빈도와 역문서 빈도를 곱한 값이다. 단어 빈도와 역문서 빈도의 값을 산출하는 방식은 여러 가지가 있다.
우선 단어 빈도 tf(t,d) 값을 산출하기 위해 총 빈도, 불린(Boolean) 빈도, 로그(Logarithm) 스케일 빈도, 증가 빈도를 사용하는 방법이 있다. ① 총 빈도는 가장 대중적인 방법으로 단순히 문서 내에서 나타나는 특정 단어의 총 빈도수를 사용하는 방법이다. 문서 d 내에서 단어 t의 총 빈도를 f(t,d)라고 할 때, 이 산출 방식은 tf(t,d) = f(t,d)로 표현한다. ② 불린 빈도는 tf(t,d) = t가 d에 한 번 이상 나타나면 1, 아니면 0이다. ③ 로그 스케일 빈도는 tf(t,d) = log (f(t,d) + 1)의 식을 사용한다. ④ 증가 빈도는 가장 빈도가 높은 단어를 분모로 target 단어의 TF를 나눈 값이며, 문서의 길이가 상대적으로 길어질 경우 단어의 빈도 값을 조절하기 위해 사용된다.
그리고 역문서 빈도 idf(t,d) 값은 한 단어가 문서 집합의 전체에서 얼마나 공통적으로 나타나는지를 나타내는 값이며, 전체 문서 수를 특정 단어를 포함한 문서의 수로 나눈 후 로그를 취하여 얻을 수 있다.
이때, 는 문서 집합 D의 크기 또는 전체 문서의 수를 의미하며, 는 단어 t가 포함된 문서의 수를 의미하므로 tf(t,d)는 0이 아니다. 단어가 전체 말뭉치 안에 존재하지 않을 경우 분모가 0이 된다. 이를 방지하기 위해 로 써야하지만, 생략하고 계산할 수 있다.결과적으로 TF-IDF 방식의 표기는 다음과 같다.
TF-IDF의 값을 이용하면 모든 문서에 흔하게 나타나는 단어를 걸러낼 수 있다. IDF의 로그 함수값은 항상 1 이상이므로 IDF와 TF-IDF값은 항상 0 이상이다. 특정 단어를 포함하는 문서들이 많을수록 로그 함수 내 값이 1에 가까워지고, IDF와 TF-IDF값은 0에 가까워진다.
예시[편집]
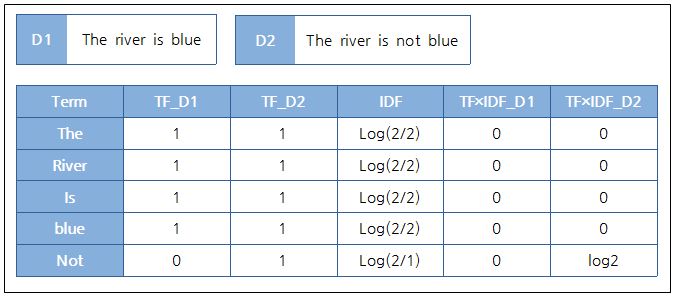
D2 문서의 Not만 log2로 값이 나오게 된다. 즉 Not이라는 특정 단어가 D2 문서와 관계가 높다는 사실을 알 수 있다.
참고 자료[편집]
- 조원호, 〈(ML) N-gram, stop word, BoW, TF-IDF 개념〉, 《네이버 블로그》, 2018-12-29
- "[1]", 위키백과'’
- "[2]", Wikipedia'’
- Rachy, 〈텍스트 분석 방법(BOW, Word2Vec, TF-IDF)〉, 《네이버 블로그》, 2018-05-27
- 이성규 기자, 〈(블로터10th) 언론사가 알아야 할 알고리즘③ TF-IDF〉, 《블로터》, 2016-09-28
같이 보기[편집]
| ||||||||||||||||||||||||||||||||||

 위키원
위키원