"해시충돌"의 두 판 사이의 차이
잔글 (→해시충돌 시, 해시테이블에서의 해결법) |
fshiel8165 (토론 | 기여) |
||
| 1번째 줄: | 1번째 줄: | ||
| − | '''해시충돌'''이란 서로 다른 | + | '''해시충돌'''이란 [[해시함수]]가 서로 다른 두 개의 입력값에 대해 동일한 출력값을 내는 상황을 의미한다. 해시충돌은 해시함수를 이용한 [[자료구조]]나 [[알고리즘]]의 효율성을 떨어뜨리기 때문에, 해시함수는 해시충돌이 자주 발생하지 않도록 구성되어야 한다. 특히, 암호학적 해시함수의 경우 해시함수의 안정성을 깨뜨리는 충돌공격이 가능할 수 있기 때문에 의도적인 해시충돌을 만드는것이 어렵도록 설계되어야 한다. |
| − | ==개요== | + | == 개요 == |
| − | |||
| − | |||
| − | + | 입력값은 다른데 출력값이 같다는 것은 특정 키의 버켓에 [[데이터]]가 집중된다는 것을 의미하기 때문에 해시 충돌은 [[해시테이블]]의 성능을 저하시킨다. | |
| − | [[ | + | [[해시테이블]]에서 사용 가능한 모든 키의 숫자는 [[테이블 인덱스]]의 개수보다 많기 때문에 불가피한 충돌을 야기하고, 그렇기 때문에 해시충돌을 피할 수 있는 [[해시 알고리즘]]은 없다. |
| − | === | + | == 원인 == |
| − | |||
| − | == | + | === 비둘기집 원리 === |
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | 대부분의 해시 알고리즘들은 항상 고정된 길이의 결과 문자열을 반환한다는 특징을 가지고 있다. 대표적인 해시 알고리즘인 [[MD5]]로 예를 들면, 128비트로 구성된 결과값, 즉 32자리의 16진수 값을 반환한다. 이 문자열의 길이는 변하지 않는다. 한 비트 단위는 0 혹은 1이라는 두 가지 경우의 수를 가진다는 점에서 128비트는 총 <math>2^{128}</math>만큼의 경우의 수를 표현할 수 있다. 이는 약 340 간(<math>10^{36}</math>)에 해당하는 매우 큰 숫자이다. 단순히 무차별 대입으로 해시 결과가 동일한 두 입력 값을 찾기 위해서는 개인용 컴퓨터로는 상당히 많은 시간을 필요로 하게 된다. 하지만 아무리 큰 숫자라고 하더라도 무한은 아니라는 점에서 특정한 두 입력 값의 결과 해시 값이 동일한 경우가 발생할 수 있다. 예를 들어 입력 값의 개수가 <math>2^{128}</math>를 넘어가게 되면 최소한 한 쌍의 입력 값은 그 결과 값이 동일할 것이다. 더 간단히 설명하자면 비둘기가 5마리일때 상자가 4개밖에 존재하지 않는다면 아무리 비둘기를 균등하게 분배해도 최소한 한 상자에는 2마리의 비둘기가 들어가게 된다. 이러한 원리를 비둘기집 원리라고 말한다. 이 원리에 따라 해시에서는 '서로 다른 입력 값의 해시 결과 값이 동일한 문제' 즉, [[해시 충돌]]이 발생할 여지가 있다. <ref>비트웹 편집국장, 〈[http://www.bitweb.co.kr/m/view.php?idx=360 블록체인의 기본, 해시란 무엇인가?]〉, 《비트웹》, 2018-02-12</ref> |
| − | + | ||
| − | + | === Birthday Paradox === | |
| − | + | ||
| + | [[파일:birthday_paradox.png|썸네일|300픽셀|생일 패러독스]] | ||
| + | |||
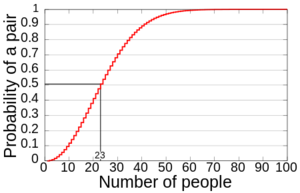
| + | [[생일 패러독스]](Birthday Paradox)란 366명의 사람이 모였을 때, 생일이 겹치는 사람이 최소 2명이 넘는다는 것으로, 가짓수를 넘어서는 통계 표본이 존재할 때, 중복되는 값이 필연적으로 발생한다는 것이다. 얼핏 생각하기에는 생일이 365가지 이므로, 임의의 두 사람의 생일이 같을 확률은 1/365이고, 따라서 365명쯤은 모여야 생일이 같은 경우가 있을 것이라고 생각하기 쉽다. 그러나 실제로는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50%를 넘고, 57명이 모이면 99%를 넘어간다. 생일 패러독스와 비슷하게 암호학적 해시결과가 같은 두 입력값을 찾는것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시충돌을 찾을 수 있다. 이러한 암호 공격을 [[생일 공격]]이라고 부른다.<ref>위키피디아 - https://ko.wikipedia.org/wiki/%EC%83%9D%EC%9D%BC_%EB%AC%B8%EC%A0%9C</ref> | ||
| + | |||
| + | == 충돌 예방법 == | ||
| + | |||
| + | === 체이닝 === | ||
| + | |||
| + | [[파일:chaining.png|썸네일|400픽셀|체이닝]] | ||
| + | |||
| + | 충돌을 허용하지만 이를 최소화 하기 위한 방법 중 하나가 바로 체이닝 방식이다. 체이닝이란 이름 그대로 데이터들을 포인터를 이용해 서로 체인 형태로 엮어 나가는 것을 뜻하며, 해시 테이블에선 동일한 해시값이 출력되 충돌이 일어나면, 그 위치에 있던 데이터에 키값을 포인터로 뒤이어 연결한다. 따라서 최초로 저장된 데이터를 시작으로 그 이후의 값이 출력되는 데이터는 모두 연결 리스트의 형태를 취한다. 그렇기 때문에 최초의 위치를 탐색하는 해시과정을 제외하고, 모든 탐색, 삽입, 삭제 과정은 연결리스트와 유사한 방식으로 진행된다. 체이닝 방법에서의 수행시간은 삽입 시에는 해시값을 이용해 바로 슬롯에 저장하면 되므로 상수시간에 일어나고, 삭제는 연결리스트의 삭제와 동일하게 상수시간에, 탐색시에는 연결리스트를 따라 가기 때문에 리스트의 길이 만큼 발생하지만, 최악의 경우 즉, 모든 데이터의 해시값이 일치하여 한 인덱스에 저장됬을 경우엔 연결리스트의 탐색시간과 동일한 선형시간을 가지게 된다. | ||
| + | |||
| + | === Open Addressing === | ||
| + | |||
| + | Open Addressing은 키값을 테이블에 저장하는 Direct Addressing Table과는 다르게, 모든 데이터를 테이블에 저장하는 방식이다. 데이터를 직접 모두 읽어 오기 때문에, 포인터를 쓸 일이 없어 포인터를 사용함으로써 발생할 수 있는 오버헤드를 방지할 수 있고, 포인터가 필요없기 때문에 구현이 훨씬 용이해졌으며, 포인터 접근에 필요한 시간이 없기 때문에 큰 성능 향상이 있다. | ||
| + | |||
| + | ==== 선형탐사 ==== | ||
| + | |||
| + | 포인터를 사용하지 않기 때문에, 다른 방법으로 충돌시에 대처해야 하는데 그 중 하나가 선형탐사이다. 선형탐사는 키값으로 인덱스를 계산할 때, 만약 충돌이 발생한다면 바로 다음 인덱스에 데이터를 저장하는 방식이다. 다음으로 이동한 후에도 충돌이 발생했다면 또 다시 바로 다음 인덱스에 저장한다. 즉, 충돌이 일어나지 않을 때 까지 계속해서 다음 인덱스로 이동을 해가며 빈 공간을 찾아 그 위치에 저장하는 방식이다. 이러한 방식은 충돌이 나면 뒤에 있는 슬롯에 데이터를 넣어 하나의 데이터 덩어리를 이루기 때문에, 데이터들의 특정 위치에만 밀집하는 현상인 primary clustering이 일어날 수 있다. 슬롯이 점점 많아지면 많아질수록 탐색 하는데 걸리는 시간이 엄청나게 많이 소요되게 되는 것이다. | ||
| + | |||
| + | ==== 제곱탐사 ==== | ||
| + | |||
| + | 제곱탐사는 primary clustering을 방지하기 위해 해시함수를 2차식의 형태로 만드는 것이다. 선형탐사와는 달리 2차식의 형태를 취했기 때문에 한 칸씩 이동하는 것이 아닌 <math>n^{2}</math>칸 만큼 이동하는 방식이다(n은 충돌 횟수). 하지만 처음 시작 해시값이 같을 경우, 그 이후의 해시값들도 모두 동일한 값으로 계산되어 충돌이 반복적으로 일어나는 secondary clustering이라는 단점이 있다.<ref>화투, 〈[https://hsp1116.tistory.com/35 해시 알고리즘 요약정리, 태스트 코드]〉, 《티스토리》, 2016-04-12</ref> | ||
| + | |||
| + | |||
| + | ==== 이중해시 ==== | ||
| + | |||
| + | 제곱탐사의 탐사할 해시값의 규칙성을 없애버려서 clustering을 방지하는 방법이다. 2개의 해시함수를 준비해서 하나는 최초의 해시값을 얻을 때, 또 다른 하나는 해시충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용한다. 이렇게 되면 최초 해시값이 같더라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라고 최초 해시값이 달라져 clustering을 모두 완화할 수 있다. | ||
| + | |||
| + | 예) 해시값을 반환해주는 <math>h_{1}</math>을 3으로 나눈 나머지, 탐사 이동폭을 결정해주는 <math>h_{2}</math>를 5로 나눈 나머지라고 할 때, 키가 3,6인 데이터의 최초 해시값은 모두 0이된다. 하지만 키가 3인 데이터의 탐사이동폭은 3, 키가 6인 데이터의 이동폭은 1로 달라진다. 반대로 키가 6,11인 데이터의 탐사이동폭은 모두 1이된다. 하지만 키가 6인 데이터의 최초 해시값은 0, 키가 11인 데이터의 최초 해시값은 2로 달라지게 된다. | ||
| + | |||
| + | 단, 제수(나누는 값)는 서로소이어야 원하는 효과를 볼 수 있다는 제약이 있다.<ref>ratsgo, 〈[https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/ 해싱, 해시함수, 해시테이블]〉, 《개인 블로그》, 2017-10-25</ref> | ||
{{각주}} | {{각주}} | ||
==참고자료== | ==참고자료== | ||
| + | |||
| + | * 비트웹 편집국장, 〈[http://www.bitweb.co.kr/m/view.php?idx=360 블록체인의 기본, 해시란 무엇인가?]〉, 《비트웹》, 2018-02-12 | ||
| + | * 화투, 〈[https://hsp1116.tistory.com/35 해시 알고리즘 요약정리, 태스트 코드]〉, 《티스토리》, 2016-04-12 | ||
| + | * ratsgo, 〈[https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/ 해싱, 해시함수, 해시테이블]〉, 《개인 블로그》, 2017-10-25 | ||
==같이 보기== | ==같이 보기== | ||
| + | |||
* [[해시]] | * [[해시]] | ||
* [[해시맵]] | * [[해시맵]] | ||
2019년 7월 26일 (금) 17:28 판
해시충돌이란 해시함수가 서로 다른 두 개의 입력값에 대해 동일한 출력값을 내는 상황을 의미한다. 해시충돌은 해시함수를 이용한 자료구조나 알고리즘의 효율성을 떨어뜨리기 때문에, 해시함수는 해시충돌이 자주 발생하지 않도록 구성되어야 한다. 특히, 암호학적 해시함수의 경우 해시함수의 안정성을 깨뜨리는 충돌공격이 가능할 수 있기 때문에 의도적인 해시충돌을 만드는것이 어렵도록 설계되어야 한다.
목차
개요
입력값은 다른데 출력값이 같다는 것은 특정 키의 버켓에 데이터가 집중된다는 것을 의미하기 때문에 해시 충돌은 해시테이블의 성능을 저하시킨다. 해시테이블에서 사용 가능한 모든 키의 숫자는 테이블 인덱스의 개수보다 많기 때문에 불가피한 충돌을 야기하고, 그렇기 때문에 해시충돌을 피할 수 있는 해시 알고리즘은 없다.
원인
비둘기집 원리
대부분의 해시 알고리즘들은 항상 고정된 길이의 결과 문자열을 반환한다는 특징을 가지고 있다. 대표적인 해시 알고리즘인 MD5로 예를 들면, 128비트로 구성된 결과값, 즉 32자리의 16진수 값을 반환한다. 이 문자열의 길이는 변하지 않는다. 한 비트 단위는 0 혹은 1이라는 두 가지 경우의 수를 가진다는 점에서 128비트는 총 만큼의 경우의 수를 표현할 수 있다. 이는 약 340 간()에 해당하는 매우 큰 숫자이다. 단순히 무차별 대입으로 해시 결과가 동일한 두 입력 값을 찾기 위해서는 개인용 컴퓨터로는 상당히 많은 시간을 필요로 하게 된다. 하지만 아무리 큰 숫자라고 하더라도 무한은 아니라는 점에서 특정한 두 입력 값의 결과 해시 값이 동일한 경우가 발생할 수 있다. 예를 들어 입력 값의 개수가 를 넘어가게 되면 최소한 한 쌍의 입력 값은 그 결과 값이 동일할 것이다. 더 간단히 설명하자면 비둘기가 5마리일때 상자가 4개밖에 존재하지 않는다면 아무리 비둘기를 균등하게 분배해도 최소한 한 상자에는 2마리의 비둘기가 들어가게 된다. 이러한 원리를 비둘기집 원리라고 말한다. 이 원리에 따라 해시에서는 '서로 다른 입력 값의 해시 결과 값이 동일한 문제' 즉, 해시 충돌이 발생할 여지가 있다. [1]
Birthday Paradox
생일 패러독스(Birthday Paradox)란 366명의 사람이 모였을 때, 생일이 겹치는 사람이 최소 2명이 넘는다는 것으로, 가짓수를 넘어서는 통계 표본이 존재할 때, 중복되는 값이 필연적으로 발생한다는 것이다. 얼핏 생각하기에는 생일이 365가지 이므로, 임의의 두 사람의 생일이 같을 확률은 1/365이고, 따라서 365명쯤은 모여야 생일이 같은 경우가 있을 것이라고 생각하기 쉽다. 그러나 실제로는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50%를 넘고, 57명이 모이면 99%를 넘어간다. 생일 패러독스와 비슷하게 암호학적 해시결과가 같은 두 입력값을 찾는것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시충돌을 찾을 수 있다. 이러한 암호 공격을 생일 공격이라고 부른다.[2]
충돌 예방법
체이닝
충돌을 허용하지만 이를 최소화 하기 위한 방법 중 하나가 바로 체이닝 방식이다. 체이닝이란 이름 그대로 데이터들을 포인터를 이용해 서로 체인 형태로 엮어 나가는 것을 뜻하며, 해시 테이블에선 동일한 해시값이 출력되 충돌이 일어나면, 그 위치에 있던 데이터에 키값을 포인터로 뒤이어 연결한다. 따라서 최초로 저장된 데이터를 시작으로 그 이후의 값이 출력되는 데이터는 모두 연결 리스트의 형태를 취한다. 그렇기 때문에 최초의 위치를 탐색하는 해시과정을 제외하고, 모든 탐색, 삽입, 삭제 과정은 연결리스트와 유사한 방식으로 진행된다. 체이닝 방법에서의 수행시간은 삽입 시에는 해시값을 이용해 바로 슬롯에 저장하면 되므로 상수시간에 일어나고, 삭제는 연결리스트의 삭제와 동일하게 상수시간에, 탐색시에는 연결리스트를 따라 가기 때문에 리스트의 길이 만큼 발생하지만, 최악의 경우 즉, 모든 데이터의 해시값이 일치하여 한 인덱스에 저장됬을 경우엔 연결리스트의 탐색시간과 동일한 선형시간을 가지게 된다.
Open Addressing
Open Addressing은 키값을 테이블에 저장하는 Direct Addressing Table과는 다르게, 모든 데이터를 테이블에 저장하는 방식이다. 데이터를 직접 모두 읽어 오기 때문에, 포인터를 쓸 일이 없어 포인터를 사용함으로써 발생할 수 있는 오버헤드를 방지할 수 있고, 포인터가 필요없기 때문에 구현이 훨씬 용이해졌으며, 포인터 접근에 필요한 시간이 없기 때문에 큰 성능 향상이 있다.
선형탐사
포인터를 사용하지 않기 때문에, 다른 방법으로 충돌시에 대처해야 하는데 그 중 하나가 선형탐사이다. 선형탐사는 키값으로 인덱스를 계산할 때, 만약 충돌이 발생한다면 바로 다음 인덱스에 데이터를 저장하는 방식이다. 다음으로 이동한 후에도 충돌이 발생했다면 또 다시 바로 다음 인덱스에 저장한다. 즉, 충돌이 일어나지 않을 때 까지 계속해서 다음 인덱스로 이동을 해가며 빈 공간을 찾아 그 위치에 저장하는 방식이다. 이러한 방식은 충돌이 나면 뒤에 있는 슬롯에 데이터를 넣어 하나의 데이터 덩어리를 이루기 때문에, 데이터들의 특정 위치에만 밀집하는 현상인 primary clustering이 일어날 수 있다. 슬롯이 점점 많아지면 많아질수록 탐색 하는데 걸리는 시간이 엄청나게 많이 소요되게 되는 것이다.
제곱탐사
제곱탐사는 primary clustering을 방지하기 위해 해시함수를 2차식의 형태로 만드는 것이다. 선형탐사와는 달리 2차식의 형태를 취했기 때문에 한 칸씩 이동하는 것이 아닌 칸 만큼 이동하는 방식이다(n은 충돌 횟수). 하지만 처음 시작 해시값이 같을 경우, 그 이후의 해시값들도 모두 동일한 값으로 계산되어 충돌이 반복적으로 일어나는 secondary clustering이라는 단점이 있다.[3]
이중해시
제곱탐사의 탐사할 해시값의 규칙성을 없애버려서 clustering을 방지하는 방법이다. 2개의 해시함수를 준비해서 하나는 최초의 해시값을 얻을 때, 또 다른 하나는 해시충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용한다. 이렇게 되면 최초 해시값이 같더라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라고 최초 해시값이 달라져 clustering을 모두 완화할 수 있다.
예) 해시값을 반환해주는 을 3으로 나눈 나머지, 탐사 이동폭을 결정해주는 를 5로 나눈 나머지라고 할 때, 키가 3,6인 데이터의 최초 해시값은 모두 0이된다. 하지만 키가 3인 데이터의 탐사이동폭은 3, 키가 6인 데이터의 이동폭은 1로 달라진다. 반대로 키가 6,11인 데이터의 탐사이동폭은 모두 1이된다. 하지만 키가 6인 데이터의 최초 해시값은 0, 키가 11인 데이터의 최초 해시값은 2로 달라지게 된다.
단, 제수(나누는 값)는 서로소이어야 원하는 효과를 볼 수 있다는 제약이 있다.[4]
각주
- ↑ 비트웹 편집국장, 〈블록체인의 기본, 해시란 무엇인가?〉, 《비트웹》, 2018-02-12
- ↑ 위키피디아 - https://ko.wikipedia.org/wiki/%EC%83%9D%EC%9D%BC_%EB%AC%B8%EC%A0%9C
- ↑ 화투, 〈해시 알고리즘 요약정리, 태스트 코드〉, 《티스토리》, 2016-04-12
- ↑ ratsgo, 〈해싱, 해시함수, 해시테이블〉, 《개인 블로그》, 2017-10-25
참고자료
- 비트웹 편집국장, 〈블록체인의 기본, 해시란 무엇인가?〉, 《비트웹》, 2018-02-12
- 화투, 〈해시 알고리즘 요약정리, 태스트 코드〉, 《티스토리》, 2016-04-12
- ratsgo, 〈해싱, 해시함수, 해시테이블〉, 《개인 블로그》, 2017-10-25
같이 보기

 위키원
위키원