디지털서명

디지털서명(digital signature)이란 첨단 기술로 보안이 강화된 전자서명의 한 종류로서, 개인키와 공개키 암호(비대칭 암호화라고도 불림)을 이용한 전자서명이다. 송신자의 개인키를 사용하여 서명을 보내면 수신측에서는 송신자의 공용키를 이용해 보내온 메시지를 해독한 다음 이를 보관하게 되고, 송신자는 디지털서명을 통해 본인임을 인증, 수신인은 해당 메시지가 위,변조 되지 않았음을 확인한다. 그리고 블록체인에 기록되는 데이터의 보안 및 무결성을 보장하는 주요 측면 중 하나이다.

예를 들어 송신자(A), 수신자(B)라 칭하게 된다면, A는 B에게 데이터를 보낼 때 A의 개인키로 문서를 암호화 하여 B에게 보내고 B는 A의 공개키로 복호환 한 후, 그것이 정말 A가 보낸 것이 맞는지 확인을 하는 방식이 디지털서명이다.

역사

디지털서명은 휘트필드 디피(Whitfield Diffie)와 마틴 헬만(Martin Hellman)이 1976년 처음으로 설명했다. 하지만 그것은 아직 확실하지 않은 추측이었다. 그 이후 로널드 리베스트 (Ron Rivest)와 아디 샤미어 (Adi Shamir), 레오나르도 아델만(Leonard Adleman)이 디지털서명에 사용될 수 있는 RSA 알고리즘을 발명하였다. 하지만 아직까지도 개념만 증명하는 단계였다. 디지털서명을 제공하기 위하여 처음으로 판매된 소프트웨어는 Lotus Notes 1.0 이었고 RSA 알고리즘을 사용하여 제작되었고 1989년에 출시되었다. 그 이후로 계속해서 디지털서명 기법이 개발되었는데, Lamport 서명부터 머클서명, Rabin 서명 등이 개발되었다.

정의

디지털서명은 일반적으로 3개의 알고리즘으로 구성이 된다.

• 키 생성 알고리즘 : 개인키를 임의로 가능한 개인키들의 세트로부터 알고리즘은 개인키와 해당 공개키를 출력한다.
• 서명 생성 알고리즘 : 서명을 만들기 위해 데이터와 개인키를 결합한다.
• 서명 검증 알고리즘 : 서명을 확인하고 메시지, 공개키 및 서명을 기반으로 메시지가 인증되었는지 여부를 확인한다.

디지털 서명은 두가지의 주요 속성이 필요하다. 첫번째로는 고정 된 메시지 및 고정 된 개인키로부터 생성된 서명의 신뢰성은 대응하는 공개키를 사용함으로써 검증이 될 수 있다는것이고, 두번째로는 당사자의 개인키를 알고 있다 하더라도 유효한 서명을 생성하는 것은 불가능하다는 것이다.

알고리즘의 핵심 기능

• 공개키 또는 암호화 된 데이터를 기반으로 개인키를 만드는 것은 절대로 불가능하다.
• 공개키를 통해 확인 된 메시지 및 개인키를 기반으로 서명의 신뢰성을 보장한다.

특징

디지털 서명은 데이터의 신뢰성을 확인하는 데 사용되는 암호화 출력이고,서명 키를 사용하여 원시 데이터에 대한 서명을 생성하는 서명 작업, 서명 키를 알지 못하는 사람이 서명을 검증할 수 있는 확인 작업 이 있으며, 디지털 서명은 공개 키 암호화라고도 하는 비대칭 암호화를 사용한다. 비대칭 키는 공개 키/비공개 키 쌍으로 구성되며, 비공개 키는 서명을 만드는 데 사용되고, 해당 공개 키는 서명을 확인하는 데 사용된다. 메시지 인증 방식은 송수신자의 메시지 교환을 제3자로 부터 보호할수 있다. 그러나 송수신자 간의 서로를 보호할 수 없다. A가 B에게 메시지 M을 보냈는데 B가 M을 위조하여 N을 받았다고 주장할 수 있다. 혹은 A가 B에게 메시지 M을 보내놓고 그런 메시지를 보낸 적이 없다고 부정할수 있다. 즉 메시지 인증 방식은 신뢰가 깨진 상태에는 대응을 못한다. 디지털 서명이 제공한다, 저자, 날짜 및 서명 시간, 메시지 내용 인증, 분쟁 해결을 위한 제 3자의 확인 이 있다. 비트 패턴은 서명된는 메시지에 의존된다. forgery 와 denial을 방지하기 위해 송신자의 고유한 정보를 사용해야 하고 서명을 만드는 것이 쉬워야 하고 쉽게 인식하고 증명해야 하며, 계산상 불가능 하도록 위조를 못하게 해야 한다. 기존 디지털 서명에 새로운 메시지로 바꿀수없고, 주어진 메시지에 대한 사기성 디지털 서명을 만들 수 없으며, 저장소에 디지털 서명의 사본을 보관하는 것이 실용적이다.

• 디지털 서명 워크플로(Digital Signature Workflow)

서명을 만들고 검증하기 위한 이 워크플로는 데이터 서명자와 데이터 수신자의 두 참가자로 구성되어 있다.

1. 서명자가 디지털 서명을 지원하는 비대칭 키를 만든다.
2. 서명자는 이 키를 사용하여 여러 서명을 만들 수 있다.
3. 서명자가 데이터에서 비공개 키 작업을 수행하여 디지털 서명을 만든다.
4. 서명자가 데이터 및 디지털 서명을 데이터 수신자에게 제공 한다.
5. 수신자가 서명자의 공개 키/비공개 키 쌍에서 공개 키 부분을 사용하여 디지털 서명을 확인하고, 확인에 실패하면 데이터가 변경된다.

디지털 서명 방식

1. Direct Digital Signature : 공개키 암호 알고리즘과 hash function 을 사용한 모델 송수신자만 존재하는 디지털 서명 구조 수신자는 송신자의 공개키 를 가지고 있다고 가정 하면, 송신자의 개인키로 전체메시지 또는 해시에 서명하고 서명후 수신자의 공개키로 암호화 한다. 대표적인 예로 ELGamal Digital Signature, Schnoor Digital Signature 가 있고 송신자의 개인키 안전성에 따라 유효성이 다라지거나 송신자가 개인키를 분실하거나 도난당했다고 거짓주장 하거나, 실제로 송신자의 개인키가 도난당할 수 있으며, 제3자의 개입이 필요하다는 문제점이 있다.
2. Arvitrated Digital Signature : 관용암호 알고리즘과 중재자를 사용한 모델 arbiter(중재자) 가 등장한다. arbiter는 서명된 메시지의 유효성을 검사한다. 이를 위해 중재자에 대한 적절한 신뢰가 필요하고, 개인키나 공개키 알고리즘 어디에서든 구현 가능하며, arbiter 는 메시지를 보거나 안볼수 있다.

• ELGamal Digital Signature

A : 송신자, B : 수신자 라고 하자

1. 소수 q와 primitive root a 선택
2. 송신자는 비밀키(개인키, X_A) 선택 후 고개키 계산(1<=X_A<p-1,A : 송신자)
3. 메시지 M을 hash 적용시켜 m으로 만든다. 0<= m <=q-1
4. 임의의 값 K선택한다.(1<=K<=q-1,gcd(k,q-1)=1)
5. 서명값 S_1,S_2 계산후 수신자에게 m과 서명값을 전달한다. $S_{1}=a^{k}modq,K^{-1}mod(q-1)$ 계산 $S_{2}=K^{-1}(m-X_{A}S_{1}mod(q-1))$
6. 수신자는 서명값 계산을 통해 검증하고, V_1,V_2 가 일치하면 유효한 것이다. $V_{1}=a^{m}modeq,V_{2}=Y_{A}^{S_{1}}S_{1}^{S_{2}}modq$

• Schnoor Digital Signature : 쉬노아 서명으로 서명값이 짧다는 특징이 있다.

전자서명과의 차이점

• 전자서명 : 전자서명은 계약 또는 기타 기록에 첨부되거나 관련이있는 문서의 내용이나 조건을 확인하는데 주로 사용된다.
• 디지털서명 : 디지털서명은 서명을 한 사람이 본인이 맞는지, 문서의 내용이 위조 혹은 변조가 된것은 아닌지 확인하는데 주로 사용된다.

작동방법

디지털서명을 만드는 가장 일반적인 방법은 PKC (Public Key Cryptography)를 사용하는 것이다. 그리고 PKC 를 제공하는데 사용되는 시스템은 PKI (Public Key Infrastructure) 라고 한다. 디지털서명 삭제및 지우기 디지털 서명은 PDF 문서에서 삭제할 수 있지만 서명 확인을 잃게 된다. 서명 필드는 서명을 지운 후에도 남아 있지만 문서의 보안 설정에 따라 제거할 수 있다.

• 서명 필드를 지우기 : 서명필드를 지우는 방법은 2가지가 있다.

첫번째 방법, [손 도구] 또는 [문서 서명] 도구를 사용하여 서명 필드를 마우스 오른쪽 단추로 클릭하고 상황에 맞는 메뉴에서 [서명 필드 지우기]를 선택한다.

두번째 방법, [서명] 패널을 열고 지우려는 서명 필드를 선택한 다음 마우스 오른쪽 단추로 클릭하거나 [옵션] 메뉴에서 [서명 필드 지우기]를 선택한다.

• 현재 문서의 모든 서명 필드 지우기 : 서명 필드 지우기는 영구적이므로 이 작업은 취소할 수 없다.

1. 검토 모드의 [보안] > [서명/인증] > [서명/인증] 메뉴에서 또는 왼쪽 도구 모음에 있는 [서명] 패널의 [옵션] 메뉴에서 [모든 서명 필드 지우기]를 합니다.
2. 메시지가 표시되면 [확인]을 클릭하여 모든 서명 필드를 지운다.

• 서명 필드 삭제 : 우선 서명필드를 지우고, 서명 필드를 마우스 오른쪽 단추로 클릭하고 상황에 맞는 메뉴에서 [서명 필드 삭제]를 선택 한다.

디지털서명의 이점

디지털서명은 3가지의 주요 이점이 있다.

• 무결성 보장 : 이론적으로 보았을때, 전송되는 데이터를 해커가 보지 않아도 변경을 할 수있지만 디지털서명이 있는 데이터의 경우 이러한 상황이 발생이 된다면 서명이 무효화가 되어 암호화가 된 디지털 서명 데이터는 위,변조가 되었는지 확인을 할 수 있어 안전하다.
• 개인의 신원 보호 : 디지털서명의 소유권은 특정 사용자에게 구속력을 가지고 있어 원하는 사람과 의사 소통을 하고있는지 확인이 가능하다.
• 개인키가 개별 사용자와 연결 : 디지털서명에 부인 방지의 품질을 부여한다. 이것은 데이터에 서명 한 개인키가 그 소유자가 아닌 다른 사람에 의해 손상되거나, 사용될 일이 없다는 것이다.

주의할 점

블록체인 기술을 사용할 때 사용자는 공개키와 개인키를 가지며 둘 다 임의의 숫자와 문자열로 나타내는데 공개키는 전자 메일 주소 및 비공개 키와 비교할 수도 있기에 누구와도 개인키를 공유하지 않는것이 가장 중요하고, 개인키를 적어서 안전한 곳에 보관하는 것도 중요하다.

활용

• PoS(Proof-of-Stake)블록체인

일반적인 PoS 기반 블록 체인의 구조는 이렇다.

1. 선택된 사용자들로 구성된 위원회가 다음에 추가할 블록 B에 대해 합의된 하위 프로토콜을 실행한다.
2. 각 위원회 구성원은 B 블록에 서명 한다.
3. 충분한 수의 위원회 구성원이 블록 B에 대한 서명을 볼 경우 각 노드는 그들의 분산 원장에 블록 B를 추가 한다.

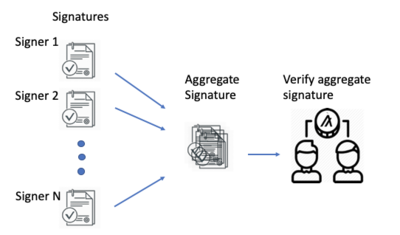
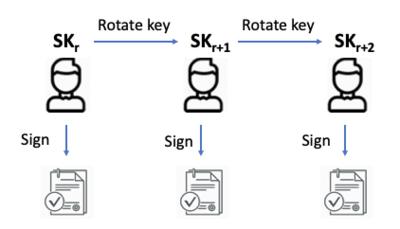
이 블록 B의 위원회 서명 컬렉션을 블록 인증서 이다. 위원회가 선택되고 서브 프로토콜이 합의되는 방식은 다양한 설계에 따라 다른 방식들도 나뉘 는데, 최근 연구에서는 알고랜드는 모든 PoS 기반 블록체인의 공통 암호화 코어인 새로운 서명 체계인 위원회가 사용하는 서명 체계를 설계했다. 효율성 측면에서 PoS 프로토콜의 주요 비용은 위원회 서명을 전파하고 블록 인증서를 저장하는 데 필요한 대역폭 및 공간과 이러한 인증서의 서명 검증에 필요한 계산 리소스이다. 보안 측면에서, 서명은 선행 보안인 키 계약 프로토콜에 의해 이행되는 선행 보안과 유사한 속성이 되어야 하고, 각 서명은 서명된 메시지 외에 현재 기간과 연결되어 있으며, 매 시간 간격 후에는 사용자의 비밀 키를 업데이트하여 이후 기간 동안만 메시지를 서명하는 데 사용할 수 있고 이전 기간에는 서명할 수 없다. 포워드 보안 서명을 사용하면 PoS 기반 블록 체인에 대한 적응형 공격을 방지할 수 있다.알고랜드의 구성을 사용하면 위원회 서명 집합(S_1, … , S_n)은 효율적으로 검증 가능한 단일 서명 S로 압축(aggregate)할 수 있으며, 라운드 r에 대한 블록에 서명한 후에는 사용자가 키를 돌려 위에서 설명한 대로 선행 보안을 충족할 수 있다. 요약하자면, 이 계획은 블록체인에서 확장 가능하고 안전한 합의를 구축하는 데 사용된다.

• Cloud KMS 디지털 서명

Cloud KMS는 디지털 서명을 위해 타원 곡선(EC) 및 RSA 알고리즘을 지원 한다. 이 두 업계 표준 알고리즘 모두 다양한 키 크기와 다이제스트 알고리즘 이며, 타원 곡선 암호법은 단방향 해시 함수 및 점 곱셈을 사용하여 타원 곡선에서 점을 계산하기 때문에 점의 곱함수를 파악하기가 어렵고, 곱함수를 파악하기 어려운 것이 EC 암호범의 암호화 이점 이다. 곡선의 크기가 클수록 곱함수를 계산하기가 더 어려워 EC 암호법의 이점은 동일한 암호화 수준을 제공하는 RSA 키에 비해 EC 키의 크기가 작다는 것이다. RSA 암호법은 큰 정수를 두 개 이상의 요소로 나누기가 어렵다는 점을 이용합니다. 키 크기가 클수록 정수를 계산하기 어렵습니다. Cloud KMS는 디지털 서명을 만들고 검증 하는데 디지털 서명을 직접 검증할 수 없다 대신 OpenSSL과 같은 공개적으로 사용 가능한 SDK 및 도구를 사용하여 디지털 서명을 검증하고 이러한 SDK와 도구에는 Cloud KMS에서 검색되는 공개 키가 필요 하다. 디지털 서명의 기능으로는

1. 키 목적이 ASYMMETRIC_SIGN인 비대칭 키를 생성할 수 있고 비대칭 서명을 위한 Cloud KMS 키는 타원 곡선 서명 알고리즘과 RSA 서명 알고리즘을 모두 지원한다.
2. 디지털 서명을 생성할 수 있다.
3. 비대칭 키의 공개 키를 검색할 수 있다.

사례

• 디지털 서명을 사용하여 빌드를 검증할 수 있다. 예를 들어 비공개 키가 디지털로 서명한 바이너리의 경우, 비공개 키에 해당하는 공개 키를 사용하여 유효성을 검사할 수 있고, 바이너리의 서명이 유효하지 않으면 바이너리가 변조되거나 손상된 것이다. 다른 예로는 인증 기관(CA)에서 발급한 인증서의 주체를 검증하는 것인데, CA는 공개 키/비공개 키의 비공개 키 부분에 대한 주체의 소유권을 바탕으로 주체에게 인증서를 발급한다. 인증서는 주체의 비공개 키로 생성된 디지털 서명을 포함하고 인증서는 공개 키/비공개 키에서 주체의 공개 키 부분도 포함하며, 주체와 상호작용하는 개체는 주체의 공개 키와 추가 인증서 확인 규칙을 사용하여 서명을 검증한다. 서명이 문제의 데이터에 상응하지 않거나 인증서에 규정된 확인 규칙을 위반하는 경우에는 서명이 유효하지 않은 것으로 판명 된다.

참고자료

• 유서트, 〈전자 서명(Electronic Signatures)과 디지털 서명(Digital Signatures)〉, 《네이버 블로그》, 2018-01-25
• 〈전자 서명과 디지털 서명의 차이〉, 《개인 블로그》
• Algorand KR, 〈지분 증명 블록체인을 위한 효율적이고 안전한 디지털 서명〉,《미디움》
• 백인감자, 〈Digital Signature(디지털서명)〉,《티스토리》, 2017-06-10
• 구글클라우드 공식 홈페이지 -〈http://a.to/19oLuJq〉
• Gaaiho Doc에서 PDF 서명 - 〈http://www.gaaiho.com/Help_Files/kor/Gaaiho_PDF_Suite_help/clearing_digital_signatures.htm〉

같이 보기

• 전자서명
• RSA
• 블록체인

이 디지털서명 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반