암호
암호(暗號, cipher)는 정보를 다른 사람이 알지 못하도록 변환한 부호를 말한다. 중요한 정보를 암호화하고 이를 복호화하기 위해 사용하는 기술을 암호기술이라고 하고, 암호기술을 연구하는 학문을 암호학이라고 한다. 암호기술의 안전성은 수학적인 원리에 기반하며, 보안에 있어서 중요한 정보를 직접적으로 보호하는 원천기술이다.
목차
개요[편집]
암호기술을 통해 보호하고자 하는 원본 데이터를 평문(plaintext)라고 하며, 평문에 암호기술을 적용한 것을 암호문(ciphertext)라고 한다. 이렇게 평문에 암호기술을 적용하여 암호문을 변환하는 과정을 암호화라고 하며, 다시 평문으로 복원하는 과정을 복호화라고 한다. 암호화하기 위해서는 암호 키가 필요하며, 키가 있어야만 암호문을 복호화할 수 있다. 그렇기 때문에 암호 키는 비밀로 유지되어야 하며 제3자가 알 수 없어야 한다. 암호기술을 이용하여 데이터 기밀성, 데이터 무결성, 인증 및 부인 방지 등의 기능을 제공할 수 있다.[1]
역사[편집]
인류의 수천 년 역사 속에서 위대한 왕과 장군들은 모두 효율적인 통신 수단에 의존해 나라를 다스리고 군대를 움직여 왔다 해도 과언이 아니다. 하지만 동시에 지도자들은 이러한 통신 내용이 적의 손에 들어가 귀중한 비밀이 누설되거나 중요한 정보가 들어가지 않을까 늘 우려했다. 그런 의미에서 적이 중요한 정보를 가로챌 수 있다는 위협이야말로 암호를 발시킨 원동력이었다고 할 수 있다. 이렇듯 비밀 보장이 절실히 필요해짐에 따라 각국 정부는 가능한 한 가장 안전한 암호를 만들어 내고, 이를 이용해 통신의 보안성을 확보하는 부서를 운영하게 된다.
이에 맞서 적국에서는 거기에 담긴 비밀을 빼내려는 암호 해독가를 동시에 양성했다. 암호 해독가들은 언어를 재료로 이용하는 연금술사로, 무작위로 모아놓은 듯한 부호에서 의미를 가진 단어를 뽑아내기 위해 일생을 바치는 신비하고도 특별한 분야의 사람들이다. 암호의 역사는 바로 암호를 만드는 사람들과 이를 해독하려는 사람들이 수백 년에 걸쳐 벌여온 전쟁의 역사이다. 지성을 무기로 한 이 군비 경쟁은 때로는 역사에 극적인 영향을 미치며 그 경로를 바꿔놓기도 했다.
암호의 어원은 그리스어의 비밀이란 뜻을 가진 크립토스(Kryptos)로 알려져 있다. 이는 평문을 해독 불가능한 형태로 변형하거나 암호화된 통신문을 원래의 해독 가능한 상태로 변환하기 위한 모든 수학적인 원리, 수단, 방법 등을 취급하는 기술이나 과학을 말한다. 즉, 암호란 중요한 정보를 다른 사람들이 보지 못하도록 하는 방법을 의미한다.
암호 기술의 발전 역사를 구분할 때 흔히 두 번의 큰 전환점을 기준으로 고대 암호, 근대 암호, 현대 암호 등의 세 단계로 나눠진다. 첫 번째 전환점은 1920년대, 1, 2차 세계 대전에서 무선 통신 기술의 발전을 기반으로 여러 가지 기계적, 전자적 암호 장치를 개발하고 사용한 것이었고, 두 번째 전환점은 1970년대 들어 컴퓨터 사용이 활발해지면서 컴퓨터를 이용한 암호 기술이 발전한 것이다.
이러한 전환점을 기준으로 고대로부터 1, 2차 세계대전 이전까지 사용된 초보적인 암호 기술들을 고대 암호라고 하면, 1970년대까지 복잡한 기계 장치와 전자 장치들을 이용한 암호 기술을 근대 암호, 컴퓨터가 개발된 이후 컴퓨터를 이용하는 암호 기술을 현대 암호라고 부른다.[2]
고대 암호[편집]
- 스테가노그래피(steganography) : 고대 봉건 사회에서는 황제나 군주가 지방 관리에게 보내는 비밀문서, 전쟁 중의 작전 지시와 보고, 첩자들과의 통신 등 전쟁이나 첩보 시에 정보를 전달해야 하는 경우에 다양한 비밀 통신 기법들이 사용되었다. 헤로도투스가 쓴 《역사》라는 책을 보면, 기원전 440년 그리스 왕 히스티아에우스(Histiaeus)가 다른 나라의 인질로 붙잡힌 상태에서 노예의 머리에 문신을 해서 글자를 새긴 후 양아들에게 밀서를 보냈다는 기록이 있다. 멀리 기밀 정보를 전달해야 하는 경우에는 사자의 머리를 깎고 메시지를 쓴 후 머리를 길러 보내면 받는 측에서는 사자의 머리를 깎고 메시지를 읽도록 하였다.[3]
- 스테가노그래피는 종이에 쓴 메시지가 그냥 보이지 않지만 불빛에 약품 처리를 하면 메시지가 나타나도록 하는 방법, 비밀 노출을 방지하기 위해 말로 전달하도록 하는 방법 등이 다양하게 사용되었다. 다만, 스테가노그래피는 만약 상대방도 이 통신 방식을 알고 있으면 비밀을 유지하기 어렵다는 한계를 갖고 있다.[2]
- 스키테일 암호 : 기원전 400년경 고대 그리스의 군사들은 스키테일 암호라고 불리는 전치 암호(Transposition cipher, 문자의 위치를 서로 바꾸는 암호)를 사용한 기록이 있다. 특정 지름을 갖는 막대에 종이를 감고 평문을 횡으로 쓴 다음 종이를 풀면 평문의 각 문자는 재배치되어 정보를 인식할 수 없게 되는데, 암호문 수신자가 송신자가 사용한 막대와 지름이 같은 막대에 종이를 감고 횡으로 읽으면 평문을 읽을 수 있다. 여기서 막대의 지름은 송신자와 수신자 사이에 공유된 비밀키가 된다.
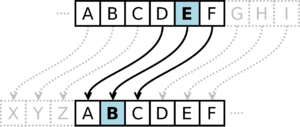
- 시저 암호 : 로마의 황제였던 줄리어스 시저(Julius Caesar)는 시저 암호라고 불리는 치환암호(substitution cipher, 문자를 다른 문자로 치환하는 암호)를 사용하였다. 시저는 가족과 비밀 통신을 할 때 각 알파벳순으로 세자씩 뒤로 물려 읽는 방법으로 글을 작성했다. 즉 A는 D로, B는 E로 바꿔 읽는 방식이었다. 수신자가 암호문을 복호화하려면 암호문 문자를 좌측으로 3문자씩 당겨서 읽으면 원래의 평문을 얻을 수 있다. 송신자와 수신자는 몇 문자씩 이동할지를 비밀키로 하여 바꿔가면서 사용할 수 있다. 시저는 브루투스(Brutus)에게 암살당하기 전 가족들로부터 다음과 같은 긴급 통신문을 받았다. 시저가 받은 편지에는 ‘EH FDUHIXO IRU DVVDVVLQDWRU’라 되어 있었다.[4] 3글자씩 당겨서 읽어보면 뜻은 ‘BE CAREFUL FOR ASSASSINATOR’, 즉 ‘암살자를 주의하라’는 것이었다. 당시 시저의 권세를 시기했던 일당은 시저를 살해할 암살 음모를 꾸미고 있었으며 시저 자신도 이를 어느 정도 눈치 채고 있었다. 하지만 시저는 구체적으로 암살자가 누구인지 알 수 없었다. 결국 암호문을 전달받은 당일 시저는 원로원에서 전혀 생각지도 못했던 브루투스에게 암살당하면서 “브루투스, 너마저…….”라는 말을 남겼다.
- 악보 암호 : 악보 암호는 전설적인 스파이 마타하리(본명 : 마그레타 G. 젤러, Margaretha Geertruida Zelle)가 사용했던 방식이다. 마타하리는 일명 ‘첩보원 H21’이란 이름으로 프랑스 장교에 접근해 군사 기밀 정보를 독일에 빼돌렸는데, 이때 비밀 통신에 사용된 암호가 악보였다. 일정한 형태의 음표에 알파벳 하나씩을 대응시킨 형태로 얼핏 보기에 평범한 악보처럼 보이지만, 실제로 연주하면 전혀 ‘음악’이 되지 않는다. 마타하리의 첩보 활동은 20여만 명에 달하는 프랑스군을 죽음으로 몰고 갔다. 그녀는 제 1차 세계 대전이 끝나기 1년 전 프랑스 정보부에 체포돼 사형을 당했다.
근대 암호[편집]


17세기 근대 수학의 발전과 함께 암호 기술도 발전하기 시작했는데, 프랑스 외교관이었던 비제네르(Vigenere)가 고안한 키워드를 이용한 복수 시저 암호형 방식, 라이언 플레이페어(Lyon Playfair)가 만든 2문자 조합 암호 등 다양한 암호 방식으로 발전하였다.[5]
20세기 들어서는 통신 기술의 발전과 기계식 계산기에 대한 연구를 바탕으로 두 차례의 세계 대전을 통해 암호 설계와 해독에 대한 필요성이 높아지면서 암호에 대한 연구가 더욱 활발하게 진행되었다. 근대 암호의 이론적 기초가 된 논문은 1920년 프리드만(Freidman)이 발표한 ‘일치 반복률과 암호 응용’과 1949년 섀넌이 발표한 ‘비밀 시스템의 통신 이론’을 들 수 있다.
섀넌은 논문에서 일회성 암호 체계가 안전함을 증명했고, 암호 체계 설계의 두 가지 기본 원칙인 ‘혼돈과 확신 이론’을 제시하였다.[6] 암호 체계를 설계함에 있어 ‘혼돈(Confusion)’은 평문과 암호문 사이의 상관관계를 숨기는 반면, ‘확산(Diffusion)’은 평문의 통계적 성격을 암호문 전반에 확산시켜 숨기는 역할을 한다. 혼돈과 확산이라는 두 가지 개념은 오늘날의 암호 체계 설계에도 여전히 적용되고 있다.
프리드만은 2차 세계 대전 중 독일군이 사용하던 에니그마(Enigma) 암호와 일본군이 사용하던 무라사끼 암호를 해독한 사람으로 유명하다. 에니그마 암호는 각기 다른 몇 개의 암호판을 전기적으로 연결하여 원문을 입력하면 전기적 연결에 의해 새로운 암호문을 출력하는 방식으로 이 기계가 존재하지 않으면 암호를 풀 수 없다.[2]
- 미드웨이 해전에서의 암호 전쟁
- 태평양 전쟁 당시 일본의 진주만 공습으로 큰 피해를 입고 전력이 약화됐던 미국은 일본의 그 다음 공격 목표가 어디인지를 알아내야 했다. 1942년 4월, 하와이 주둔 미국 해군 정보부의 암호 해독반 블랙 체임버(Black Chamber)는 일본군의 무전이 증가하고 있음을 발견했다.[7] 이미 일본 해군의 암호 체계인 JN-25를 해독하고 있던 해독반은 AF라는 문자가 자주 나타난다는 사실에 주목했다. AH는 진주만을 뜻하는 것이었다. 암호 해독반의 지휘관이었던 조셉 로슈포르(Joseph Rochefort) 중령은 AF를 미드웨이 섬이라고 생각했다. 일본의 정찰기가 ‘AF 근처를 지나고 있다’는 내용의 무선 보고를 해독한 적이 있었던 그는 정찰기의 비행경로를 추정해본 결과 AF가 미드웨이 섬일 것이라는 심증을 갖게 된 것이다.
- 로슈포르 중령은 체스터 니미츠(Chester William Nimitz) 제독에게 일본군의 침공이 임박했다는 것과 AF가 자주 언급된다는 점, 그리고 AF가 미드웨이 섬일 것이라는 보고를 한 후, 미드웨이 섬의 담수 시설이 고장 났다는 내용의 가짜 전문을 하와이로 평문 송신하게 하자고 건의했다.[3] 3월에 미드웨이 섬 근처에 일본 해군의 비행정이 정찰 왔던 것을 알고 있던 니미츠 제독은 이 건의를 받아들였다. 사실 미드웨이 섬의 정수 시설은 아무런 문제가 없었다. 이틀 후, 도청된 일본군 암호 중 ‘AF에 물 부족’이라는 내용이 해독되었다. 이로써 일본군의 다음 공격 목표가 미드웨이 섬이라는 것이 분명해진 것이다.
- 미군은 암호 해독을 통해 일본의 공격 목표가 미드웨이라는 사실을 알아낸 후 전투에 대비하고 반격을 준비하여 일본의 태평양 함대를 격파하고 전쟁을 승리로 이끌 수 있었다.[2]
현대 암호[편집]
현대 암호는 1970년대 후반 미국 스탠퍼드 대학교과 MIT 대학교에서 시작되었다. 1976년 스탠퍼드 대학교의 휫필드 디피(Whitfield Diffie)와 마틴 헬만(Martin Hellman)은 ‘암호의 새로운 방향(New Directions in Cryptography)’이라는 논문에서 처음으로 공개키 암호의 개념을 발표하였다.[4] 종래의 관용 암호 방식 또는 대칭키 암호 방식에서는 암호화키와 복호화키가 동일한 비밀키를 사용하기 때문에 송신자와 수신자는 비밀 통신을 하기 전에 비밀키를 공유하고 있어야 한다. 반면 공개키 암호 방식에서는 하나의 쌍이 되는 공개키와 비밀키를 생성하여 암호화에 사용되는 공개키는 공개하고, 복호화에 사용되는 비밀키는 사용자가 안전하게 보관하도록 한다. 공개키 암호 방식에서는 송신자와 수신자가 사전에 키를 공유할 필요가 없기 때문에 불특정 다수 사용자 간에 사전 준비가 없이도 암호 통신망을 구축하는데 유용하게 사용할 수 있다.
이어 1978년 MIT 대학의 로널드 라이베스트(Ron Rivest), 아디 샤미르(Adi Shamir), 레너드 애들먼(Leonard Adleman)은 소인수 분해 문제에 기반을 둔 RSA 공개키 암호를 개발했는데, 이것은 오늘까지도 가장 널리 사용되는 공개키 암호 방식이다. 공개키 암호의 도입은 현대 암호의 발전에 중요한 계기가 되었다.[3]
한편, 1977년 미국 상무성 표준국(NBS, 현 NIST)은 전자계산기 데이터 보호를 위한 암호 알고리즘을 공개 모집하여, IBM 사가 제안한 DES(Data Encryption Standard)를 표준 암호 알고리즘으로 채택했다. DES의 표준화를 계기로 하여 금융 시스템을 중심으로 상업용 암호화의 이용이 증가하게 되었고 컴퓨터 통신망을 이용한 문서 전송, 전자 자금 이체 등이 활성화되었으며 암호 방식이 일반인들에게 알려지고 널리 사용되는 계기가 되었다.
이전의 암호 방식에서는 사용하는 키뿐만 아니라 암호 알고리즘도 비밀로 하여 암호문의 비밀을 지키려고 하는 경우도 있었으나, 현대 암호에서는 암호 알고리즘을 공개하도록 하고 있다. 1883년 아우후스트 케르크호프스(Auguste Kerckhoff)는 암호 시스템의 안전성에 대해 ‘키 이외에 암호 시스템의 모든 것이 공개되어도 안전해야 한다’고 했는데 이것을 케르크호프스의 원리(Kerckhoff’s principle)라고 한다.[8] 이렇게 함으로써 암호 방식의 안전성을 공개적으로 검토하게 하여 안전성을 확인하는 것이다.
표준화된 암호와 표준화된 컴퓨팅 기기들을 사용하는 현대 암호에서는 암호 알고리즘을 감추기가 매우 어렵다. 또한 암호 알고리즘을 감춘다고 해서 암호의 보안성이 높아지는 것도 아니다. 비밀로 다루어진 암호 알고리즘이 일단 공개되고 나면 그 안전성에 문제가 발견되는 사례가 많다. 그러므로 암호 분야에서는 어떤 암호 알고리즘이 많은 암호 학자들에 의해 장기간 세부적으로 수행된 분석에서도 잘 견디어 낼 때까지는 그 알고리즘을 안전하다고 인정하지 않는다. 즉, 암호 체계는 ‘무죄가 증명될 때까지는 유죄’이다.[2]
차세대 암호[편집]
양자 기반 알고리즘인 쇼어 알고리즘(Shor's algorithm)은 인수분해 문제의 해결 속도를 단축시켜 RSA, ECC 등 인수분해 및 이산대수 기반의 공개키 암호 알고리즘을 더 이상 사용할 수 없게 한다. 또한, 그로버 알고리즘(Grover algorithm)은 정렬되지 않은 데이터베이스의 원소를 검색하는 속도를 향상시켜 대칭키 암호는 키 사이즈를 2배, 해시 함수의 출력길이를 3배 증가시켜야 기존의 안전성을 가질수 있게 된다.
이러한 환경의 변화같이 특정 상황에서 기존 현대 암호기술(RSA, ECC 등)이 해결하지 못하는 경우를 대비하여, 새로운 암호기술들에 대한 연구가 활발히 진행되고 있다. 양자컴퓨팅 환경에서도 안전하게 사용할 수 있는 공개키 암호 기술인 양자내성암호와 더불어, 동형암호(암호화된 상태로 연산 가능한 암호), 형태보존암호(암호문이 평문과 동일한 형태를 가지는 암호), 경량암호(계산능력이 떨어지는 사물인터넷 환경 등에서 효율적으로 사용할 수 있는 암호) 등이 있다.[2]
- 양자내성암호(Post Quantum Cryptography, PQC)
- 격자 기반(Lattice-based) : 격자(Lattice) 위에서 계산하는 문제의 어려움에 기반하는 암호 시스템
- 코드 기반(Code-based) : 일반적인 선형 코드(Linear Code)를 디코딩하는 어려움에 기반하는 암호 시스템
- 다변수 기반(Multi-variate) : 유한체(Finite Field) 위에서 계산하는 다변수 함수 문제의 어려움에 기반하는 암호 시스템
- 해시 기반(Hash-based) : 해시 함수의 안전성을 기반으로 한 전자 서명 시스템
- 아이소제니 기반(Isogeny-based) : 순서(Order)가 같은 두 타원 곡선 사이에 존재하는 아이소제니(Isogeny)를 구하는 문제의 어려움에 기반하는 암호 시스템
- 동형암호(Fully Homomorphic Encryption) : 암호문을 이용하여 계산을 할 수 있도록 해주는 공개키 암호화 방식이다. 암호화된 데이터들을 이용하여 계산한 결과를 복호화하면 암호화되지 않은 상태로 계산한 값과 일치하는 암호화 방식이다. 국내에서는 정수 환(Ring) 기반의 동형암호 알고리즘이 개발되었으며, 국외 IBM, 마이크로소프트 등은 다수의 동형암호 알고리즘을 개발하고 의료 분야 등 다양한 응용 서비스 적용 기술을 개발 중이다.[9]
- 형태보존암호(Format Preserving Encryption) : 암호문이 평문이 가지고 있는 형태를 그대로 유지한 암호화 방식이다. 암호화된 데이터들을 이용하여 계산한 결과를 복호화하면 암호화되지 않은 상태로 계산한 값과 일치하는 암호화 방식이다. 작은 크기의 평문에 대한 암호화가 가능하며, 안전성에 문제가 발생하지 않도록 추가적인 입력 정보인 트윅(Tweak)을 사용한다. 데이터의 길이가 보존되어 추가적인 저장 공간 구매가 불필요하며, DB 스키마 변경도 불필요하기 때문에 암호화 시스템 구축비용이 절감된다. 신용카드, 주민등록번호, 사회보장번호(Social Security Number, SSN) 등과 같이 특정 형태의 암호화에 효율적으로 사용할 수 있다.
종류[편집]
대칭키 암호[편집]
대칭키 암호(Symmetric-key Cryptography)는 암·복호화에 같은 암호 키를 사용하는 알고리즘이며, 송신자와 수신자는 암호 키가 노출되지 않도록 비밀로 관리해야 한다. 대칭키 암호는 내부 구조가 간단한 전치와 치환(대체)의 조합으로 되어 있어 연산 속도가 빠르다는 장점이 있다.[10] 하지만 송·수신자 간에 동일한 키를 공유해야 하므로 많은 사람들과의 정보 교환 시 많은 키를 관리해야 하는 어려움이 있다.[1][11]
- 블록암호(Block Cipher) : 블록암호는 평문을 고정된 크기의 블록단위로 암·복호화를 수행하며, 각 블록마다 동일한 키가 사용된다. 블록암호는 고정된 크기로 평문을 나누기 때문에, 원하는 길이를 맞추기 위하여 패딩(padding)이라는 기법을 이용한다. 또한 하나의 키로 여러 블록을 안전하게 처리하기 위하여 운용 방식(mode of operation)이라는 절차를 이용한다. 섀넌(Shannon)의 암호 이론에 의하면 전치와 치환(대체, 환자)를 반복시켜 평문의 통계적 성질이나 암호 키와의 관계가 나타나지 않아 안전한 암호를 구성할 수 있다.[12] 대표적인 블록암호 알고리즘으로는 국산 알고리즘인 SEED(시드), HIGHT(하이트), ARIA(아리아), LEA(레아)와 외산 알고리즘인 DES(디이에스), AES(에이이에스) 등이 있다.[1]
- 스트림 암호(Stream Cipher) : 스트림 암호는 평문과 동일한 길이의 키스트림(key stream) 수열을 생성하여, 평문과의 XOR 연산을 통하여 암·복호화를 수행한다. 키스트림 수열을 생성할 때, 평문과 독립적으로 생성하는 경우를 동기식 스트림 암호라고 하며, 반대로 평문이 키스트림 수열에 영향을 미치는 경우를 비동기식 혹은 자기동기 스트림 암호라고 한다. 구현 여건이 제약되는 환경에서 구현이 용이하며, 무선 통신 등의 환경에 주로 사용된다. 대표적인 스트림 암호 알고리즘으로 RC4, A5/1, A5/2 등이 있다.[1]
비대칭키 암호[편집]
- 공개키 암호(Public-key Encryption) : 비대칭키 암호는 공개키 암호라고도 하며, 대칭키 암호와 달리 암·복호화에 서로 다른 키를 사용하는 알고리즘이다.[13] 송신자는 수신자의 공개키를 이용하여 암호화하며, 수신자는 자신의 공개키로 암호화된 암호문을 자신의 개인키로 복호화할 수 있다. 공개키 암호는 수학적인 난제를 기반으로 설계되어 있고 암·복호화에 복잡한 수학 연산을 사용하기 때문에, 대칭키 암호에 비해 효율성이 떨어질 수 있다.[14] 하지만 여러 송신자가 하나의 공개키로 암호화를 수행하기 때문에 사용자가 많더라도 키를 관리하는 데에 유리하다. 대표적인 알고리즘으로 RSA, 엘가말, 타원곡선암호(ECC) 등이 있다.[1]
- 전자서명(Digital Signature) : 전자 서명은 인터넷 상에서 본인임을 증명하기 위해 서명을 하는 수단으로, 공개키 암호를 거꾸로 활용하는 방식이다. 송·수신자의 역할이 반대로 되어, 개인키를 소유한 사람만이 전자서명 알고리즘을 통해 평문에 대한 서명 값을 생성할 수 있다. 생성된 서명 값에 대하여 공개키를 이용하면 평문을 검증할 수 있기 때문에 누구나 그 서명을 검증할 수 있게 된다. 대표적인 전자 서명 알고리즘으로 DSA, RSA Signature, 타원곡선 디지털서명 알고리즘(ECDSA) 등이 있다.[1]
해시 함수[편집]
해시 함수(Hash Function)는 임의의 길이의 메시지를 입력으로 받아 고정된 길이의 해시 값을 출력하는 함수이다.[15] 해시 함수에는 암호 키가 사용되지 않기 때문에, 같은 입력에 대해서 항상 같은 해시 값을 얻을 수 있다. 이러한 성질로 인해 입력 메시지에 대한 변경할 수 없는 증거 값을 만들어냄으로서, 주로 무결성을 제공하는 목적으로 사용된다.[16] 안전한 해시 함수는 역상 저항성, 제2역상 저항성, 충돌 저항성을 가져야 한다.[1]
- 역상 저항성 : 어떤 해시 값에 대하여, 원래 입력 값을 찾는 것이 어려워야 하며, 이를 일방향성(One-wayness)이라고도 한다.
- 제2역상 저항성 : 어떤 입력 값에 대하여, 그 입력값의 해시 값과 같은 해시 값을 갖는 또 다른 입력값을 찾는 것이 어려워야 한다.
- 충돌 저항성 : 동일한 해시 값을 갖는 두 입력 값을 찾는 것이 어려워야 한다.
해시 함수는 데이터가 통신 중 변조되지 않았다는 무결성 검증이 필요할 때, 메시지인증코드(MAC, Message Authentication Code)의 형태로 사용될 수 있다. 또한 해시 함수는 전자서명에도 활용될 수 있다. 전체 메시지가 아닌 짧은 해시 값에 전자 서명을 계산하면 효율적으로 서명 값을 생성할 수 있다. 원래 메시지가 아닌 해시 값에 대해 서명을 하였지만 같은 해시 값을 갖는 다른 메시지를 찾는 것이 어렵기 때문에, 이 서명은 메시지에 대한 서명이라고 인정된다.[16] 대표적인 해시 함수로는 MD5, HAS-160, SHA-1, SHA-2, SHA-3 등이 있다.[1]
각주[편집]
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 〈암호기술의 정의〉, 《KISA 암호이용활성화》
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 〈암호기술의 역사〉, 《KISA 암호이용활성화》
- ↑ 3.0 3.1 3.2 duck1201, 〈암호의 역사〉,《네이버 블로그》, 2017-02-22
- ↑ 4.0 4.1 하늘바다영재교육원, 〈제 57회 Arduino_조이스틱_암호〉, 《네이버 블로그》, 2016-01-25
- ↑ mean, 〈(IT상식) #007. 암호화(Encryption)〉, 《네이버 블로그》, 2016-06-01
- ↑ 청단풍, 〈정보와 첩보 8 미 국가 안보국NSA〉, 《네이버 블로그》, 2017-04-10
- ↑ 〈미드웨이 해전〉, 《위키백과》
- ↑ 이충국, 〈암호는 수학이다〉, 《월간조선 뉴스룸》, 2016-06
- ↑ 〈2017 한국인터넷백서 Korea Internet White Paper〉, 《한국인터넷진흥원》
- ↑ 소셜리, 〈현대암호(대칭키)〉, 《네이버 블로그》, 2016-09-01
- ↑ wind1237, 〈대칭키 암호 IT/DB_IT_Info〉, 《네이버 블로그》, 2013-07-26
- ↑ 멋징승현, 〈Cryptography, 암호 이용 활성화〉, 《티스토리》, 2013-07-30
- ↑ 미니송, 〈정보보안 암호화의 기초〉, 《티스토리》
- ↑ 소셜리, 〈공개키 암호 시스템〉, 《네이버 블로그》, 2016-09-14
- ↑ weicome, 〈HashFunction 해시함수〉, 《티스토리》, 2016-10-12
- ↑ 16.0 16.1 사랑과 생각, 〈IoT 를 보안을 위한 ECC 및 하이브리드 암호화〉, 《네이버 블로그》, 2017-09-19
참고자료[편집]
- 양대일, 〈암호에 대한 이해〉, 《정보 보안 개론》, 한빛아카데미㈜, 2013-06-28
- 〈암호기술의 정의〉, 《KISA 암호이용활성화》
- 〈암호기술의 역사〉, 《KISA 암호이용활성화》
같이 보기[편집]
| ||||||||||||||||||||||||||
| ||||||||||
| ||||||||||||||||||||||

 위키원
위키원