논리연산
논리연산(逻辑运算, Logical Operation)은 주로 논리곱(AND), 논리합(OR), 논리부정(NOT) 등의 기호 논리학의 규칙에 따른 연산이다. 불 대수(Boolean algebra)는 19세기 중반 영국의 수학자 조지 불(George Boole, 1815년 11월 2일 ~ 1864년 12월 8일)이 고안하고 형식화한 대수 체계를 의미한다. 논리연산(logical operation, logical connective)으로도 불린다. 수리 논리학이나 컴퓨터공학과에서, 두 개의 상태인 참(1, T, True)과 거짓(0, F, False)으로 불 연산(Boolean expression)이라 한다. 참고로 백괴사전에서는 이 불 대수를 불(火) 대수로 해석해서 불 붙은 물건의 성질을 다루는 대수로 묘사했다. 불 대수의 출현 이후로 논리학은 기호논리학의 성향이 강해지기 시작한다.
프로그래밍에서는 조건에 의한 분기나 반복을 만드는데 이용되고, 디지털 논리 회로를 배울 때 유용하게 사용된다. 디지털 회로의 신호는 0과 1로 구성되어 있기 때문이다. 전자계통에선 논리연산을 하는 소자를 게이트(Gate)라고 하며 트랜지스터 여러 개를 조합해서 만들 수 있다.
이산수학에서는 속(Lattice) 중 Complementary Lattice이며 Distributive Lattice인 Lattice를 불 속(Boolean Lattice)이라 하며 이를 대수(Algebra)식으로 나타낸 것을 불 대수(Boolean Algebra)라고 한다. 불 속의 원소 개수는 해당 원자(atom) 개수 n에 대해 2n개이다. 즉, 불 속의 원소 개수는 2의 제곱수대로 올라간다고 보면 된다.
개요[편집]
컴퓨터에서 연산은 산술연산과 논리연산 두 가지로 나눠 볼 수 있다.
1 + 1 = 2가 되는 것을 산술연산이라고 한다.
산술연산은 숫자를 계산해 그 결과 또한 숫자가 되는거죠. 즉, 산술연산에서 1은 숫자 1(one)을, 0은 숫자 0(zero)을 의미한다. 산술연산자에는 더하기(+), 빼기(-), 곱하기(×), 나누기(/)와 같은 사칙연산자가 있다.
1 + 0 = 참 (또는 거짓)이 되는 것을 논리연산이라고 한다.
논리연산에서 1, 0과 같은 피연산자는 참, 거짓을 뜻하고 연산 결과 또한 참과 거짓이 된다. 즉, 논리연산에서 1은 참(true)을 0은 거짓(false)을 의미한다.
논리연산의 예시[편집]
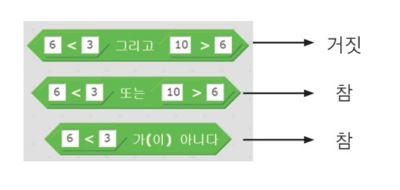
예를 들어, "6<3’그리고 '10>6'"과 같은 논리연산은 "6<3"이 거짓이고 "10>6"이 참이므로 결과는 거짓이다. "'6<3' 또는 '10>6'"과 같은 논리연산은 "6<3"이 거짓이고 "10>6"이 참이므로 결과는 참이다. 또한 "'6<3'이 아니다"와 같은 논리연산은 "6<3"이 거짓이므로 결과는 참이다. 이와 같은 논리연산을 블록 기반 프로그래밍 도구로 작성한 예는 오른쪽과 같다.
설명[편집]
논리 연산에서 처리되어지는 자료들(피연산자)은 논리값이며, 연산의 결과도 논리값이다. 주로 관계 연산들을 합성하는 데 사용되며, 관계 연산과 마찬가지로 반복 구조의 반복 조건 및 선택 구조의 조건에 사용되는데 논리 연산은 복합 조건을 만드는 데 사용된다.
"그리고"는 논리곱 연산으로 연산자 양쪽의 항목(피연산자)이 모두 참일 때만 결과가 참이며, 둘 중의 어느 하나가 거짓이거나 둘 모두가 거짓이면 결과는 거짓이 된다. "또는"은 논리합 연산으로 연산자 양쪽의 항목(피연산자)이 모두 거짓일 때만 결과가 거짓이며, 둘 중의 어느 하나가 참이거나 둘 모두가 참이면 결과는 참이 된다. "가(이) 아니다"는 논리 부정 연산으로 항목(피연산자)이 참이면 결과는 거짓이 되고, 항목(피연산자)이 거짓이면 결과는 참이 된다.
논리연산의 종류[편집]
부정 (NOT; ¬)[편집]
말 그대로 부정(否定)이다. 즉, 참과 거짓을 뒤집는다. C언어의 영향을 받은 프로그래밍 언어에서는 일반적으로 !를 부정 연산자로 사용하며, 그 외에 ~A도 많은 프로그래밍 언어에서 사용되며, 필기나 서적 등에서는 A' 또는 A 위에 ㅡ를 그려넣은 기호가 주로 쓰인다. 불 보수(Boolean Complement)로도 불린다. 이 연산을 하는 회로는 따로 보수기(inverter)라는 이름으로 불린다.
NOT 연산 결과 입력값 반환값 0 1 1 0
논리곱 (AND; ∧)[편집]
두 명제가 모두 참이어야 참값을 돌려준다. C언어의 영향을 받은 프로그래밍 언어에서는 일반적으로 &를 논리곱 연산자로 사용하며, 불 대수에서는 AND는 곱셈과 동치이다. 불 곱(Boolean Multiplication) 혹은 논리곱이라 부른다. 아래의 연산결과를 보면 왜 곱셈과 동치인지 쉽게 알 수 있을 것이다. AB 또는 A·B로 표시한다.
AND 연산 결과 입력값 반환값 0, 0 0 0, 1 0 1, 0 0 1, 1 1
논리합 (OR; ∨)[편집]
두 명제 중 어느 한 명제만 참이어도 참값을 돌려준다. C언어의 영향을 받은 프로그래밍 언어에서는 일반적으로 |를 논리합 연산자로 사용한다. 불 대수에서는 OR는 덧셈과 동치여서, 논리합(Boolean Addition)으로 부른다. 아래에서 보듯 1 + 1 = 1 임을 주의해야 한다. A+B로 표시한다.
OR 연산 결과 입력값 반환값 0, 0 0 0, 1 1 1, 0 1 1, 1 1
부정 논리곱 (NAND; ↑)[편집]
Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다.
NAND 연산 결과 입력값 반환값 0, 0 1 0, 1 1 1, 0 1 1, 1 0
부정 논리합(NOR; ↓)[편집]
두 명제 중 정확히 하나만 참이어야, 혹은 두 명제의 참거짓 여부가 다를 때 참값을 돌려준다. C언어의 영향을 받은 프로그래밍 언어에서는 ^를 배타적 논리합 기호로 사용한다. 다만 일반적인 경우에는 ^가 제곱으로 사용되기 때문에 처음 프로그래밍 언어를 배우는 사람들은 제곱을 하려고 ^ 기호를 사용했다가 안드로메다로 가는 경우가 있다.(…) 이 방식으로 특정 '키'를 이용해 암호화를 하면 그 '키'로 복호화가 가능해서, 암호화 기법으로도 널리 사용된다. 비교 대상의 비트가 0이든 1이든 상관 없이 같기만 하면 0을 돌려준다는 특성을 이용하여 어셈블리어 등의 언어에서 어떤 레지스터나 변수를 0으로 초기화할 때 사용되기도 한다.
XOR 연산 결과 입력값 반환값 0, 0 0 0, 1 1 1, 0 1 1, 1 0
동치 (EQV; =)[편집]
두 명제가 다 참이거나 다 거짓이면, 혹은 두 명제의 참거짓 값이 같으면 참값을 돌려준다. 배타적 부정 논리합 (XNOR) 또는 배타적 논리곱이라고도 한다. 수학적으로는 크로네커 델타(Kronecker delta)로 정의돼 있다. C언어 및 여기서 파생한 프로그래밍 언어에선 =는 대입을 의미하므로 =를 두개 사용해 ==로 동치를 계산한다.
EQV 연산 결과 입력값 반환값 0, 0 1 0, 1 0 1, 0 0 1, 1 1
성질[편집]
교환법칙 / 결합법칙 / 분배법칙[편집]
A+B=B+A A·B=B·A
(A+B)+C=A+(B+C) (A·B)·C=A·(B·C)
A·(B+C)=A·B+A·C A+(B·C)=(A+B)·(A+C)
산수랑 똑같다. 다만 여기서 주의할 점은 분배 법칙에서 A+(B·C)=(A+B)·(A+C)가 된다는 것이다. 드 모르간의 법칙 하단의 설명을 보면 쉽게 이해할 수 있다.
동일법칙(idempotent)[편집]
A·A = A A + A = A
계산하려는 두 숫자가 똑같으면 결과도 그 똑같은 값이 나온다는 뜻이다.
항등원(identity)[편집]
A·1 = A = 1·A A+0 = A = 0+A
흡수법칙(absorption)[편집]
A+A·B=A A·(A+B)=A
전기 회로에서 곱연산을 직렬로, 합연산을 병렬로 생각해보면 이해가 쉽다. 아래 식에서 B는 A와 병렬이라서 B가 끊어졌어도 A가 이어져 있으면 그대로 전기가 흐르기 때문에 사실상 B는 없는 것이나 다름없고, A를 직렬로 두 개 단 것과 똑같기 때문에 식이 저렇게 A로 흡수되는 것이다.
수학적 증명은
A·(A+B) A·A + A·B (∵분배법칙) A + A·B (∵동일법칙 A·A = A) A·1 + A·B (∵항등원 A·1 = A) A·(1 + B) (∵분배법칙) A·1 (∵ B + 1 = 1) A (∵항등원 A·1 = A)
위 식의 증명은 위의 증명에서 3번째 줄부터 같다.
이중부정 법칙(involution)[편집]
(A')' = A
드모르간 법칙(De Morgan law)[편집]
(A·B)'=A'+B' (A+B)'=A'·B'
식을 깔끔하게 정리할 때 가장 많이 사용되는데다가 NAND 연산, NOR 연산과 밀접한 연관이 있는 만큼 불 대수에서 상당히 중요하게 다뤄지는 성질이다. 오죽하면 대부분 교재에서 이 법칙 하나만 불 대수 파트에서 분리해서 따로 가르칠 정도.
사실 머리를 좀 굴려보면 AND와 OR은 같은 구조의 함수지만(항등원끼리연산하면 항등원, 나머지경우는 항등원이 아닌 것) AND는 항등원이 1(=0')이고 OR은 항등원이 0(=1')일 뿐이라는 걸 알 수 있는데, 다시 말해 NOT은 ({0 , 1}, AND)에서 ({0, 1}, OR)로 가는 Isomorphism이다. 이중 부정규칙을 이용하면 동시에 NOT은 ({0 , 1}, OR)에서 ({0, 1}, AND)로 가는 Isomorphism이므로 결론적으로 NOT은 ({0 , 1}, AND, OR)에서 ({0, 1}, OR, AND)로 가는(연산이 서로 바뀌었다) Isomorphism이다.
이걸 이용해 드모르간 법칙을 쉽게 증명할 수 있을 뿐만 아니라 성질 항목에 나와있는 한쌍의 공식이 서로를 유도할 수 있다는 걸 쉽게 보일 수 있다.
합의(Consensus) 법칙[편집]
AB + BC + CA' = AB + CA' (A+B)'=(A + B)(B + C)(C + A') = (A + B)(C + A')
자세히 보면 가운데 마디가 사라진 것을 볼 수 있다.
위 식의 증명은
BC 1·BC (∵항등원 A·1 = A) (A+A')·BC (∵A+A' = 1) ABC + A'BC (∵분배법칙) ABC + CA'B (∵교환법칙)
을 이용해서
AB + BC + CA' AB + ABC + CA'B + CA' (AB + AB·C) + (CA'·B + CA') (∵결합법칙) (AB + AB·C) + (CA' + CA'·B) (∵교환법칙) AB + CA' (∵흡수법칙 A+A·B=A)
아래식도 비슷하다.
그 밖의 연산 법칙[편집]
A + A' = 1 A·A' = 0
A+1=1 A·0 = 0
A+A'·B=A+B A·(A'+B)=A·B
마지막 식의 증명
A·(A'+B) A·A' + A·B (∵분배법칙) 0 + A·B (∵ A·A' = 0) A·B (∵항등원 0+A = A)
그 위의 식도 비슷하다.
연산 우선 순위[편집]
대수학에서 곱셈 연산이 덧셈 연산 보다 우선이듯이, 논리 연산에서도 논리곱(AND)이 논리합(OR) 보다 연산 순위가 높다.
분배법칙의 아래 두 식 중에 첫 번째 식의 우변에는 괄호가 없다. 이는 AND가 OR보다 연산 우선 순위가 높기 때문이다. 괄호가 생략된 것이라 보아도 되는데 A·B와 A·C에 대한 괄호의 존재 여부는 우변의 결과에 영향을 미치지 않는다.
A·(B+C)=A·B+A·C A+(B·C)=(A+B)·(A+C)
A·(B+C)=(A·B)+(A·C)=A·B+A·C
그리고 부정(NOT) 연산은 AND와 OR보다 연산 우선 순위가 높다.
결국 NOT > AND > OR의 연산 순서가 되겠다.
참고자료[편집]
같이 보기[편집]
| ||||||||||||||||||||||||||||||||||

 위키원
위키원