"블록암호"의 두 판 사이의 차이
| 1번째 줄: | 1번째 줄: | ||
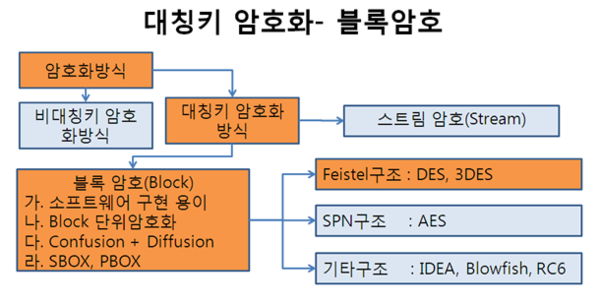
'''블록암호'''(block cipher)<!--블록 암호, block cipher, blockcipher-->란 기밀성있는 정보를 정해진 [[블록]] 단위로 [[암호화]]하는 [[대칭키]] 암호시스템이다. 만약 암호화하려는 정보가 블록의 길이보다 길 경우에는 특정한 운용모드가 사용된다.(예 : ECB, CBC, OFB, CFB, CTR) | '''블록암호'''(block cipher)<!--블록 암호, block cipher, blockcipher-->란 기밀성있는 정보를 정해진 [[블록]] 단위로 [[암호화]]하는 [[대칭키]] 암호시스템이다. 만약 암호화하려는 정보가 블록의 길이보다 길 경우에는 특정한 운용모드가 사용된다.(예 : ECB, CBC, OFB, CFB, CTR) | ||
| − | ==대칭키== | + | ==특징== |
| − | ===구조=== | + | ===패딩=== |
| + | 주어진 평문을 블록 암호로 암호화하기 위해서는 평문을 우선 블록 크기의 배수로 만들어야 합니다. 예를 들어 DES로 암호화를 한다면 평문은 <math>{64}\times{n}</math>비트이어야 한다. 평문의 길이가 블록 크기의 배수가 아닌 경우, 블록 크기의 배수가 되게끔 패딩을 추가한다. 이러한 패딩을 하는 알고리즘은 PKCS#5, ANSIX923 등이 존재한다. | ||
| + | |||
| + | 패딩의 가장 중요한 원칙은 <math>P(M)</math>으로부터 | ||
| + | M | ||
| + | 을 복구할 수 있어야 한다는 점입니다. 이 원칙이 지켜지지 않으면 패딩된 메시지로부터 원본 메시지를 찾을 수 없습니다. 예를 들어 평문의 길이를 32비트의 배수로 만들고 싶을 때 모자란 만큼 0으로 채워 32의 배수로 만드는 패딩을 생각해봅시다. 그러면 패딩된 메시지 00010011 01000111 11001000 00000000에서 실제 평문이 어디까지인지 알 수 있을까요? 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있습니다. 즉 비트 단위의 All zero 패딩은 패딩된 메시지로부터 원본 메시지를 복구할 수 없으므로 사용할 수 없는 패딩입니다. | ||
| + | |||
| + | ===대칭키=== | ||
| + | ====구조==== | ||
[[파일:대칭키 암호화-블록암호.png|600픽셀|가운데|]] | [[파일:대칭키 암호화-블록암호.png|600픽셀|가운데|]] | ||
| − | ===장단점=== | + | ====장단점==== |
* '''장점''' | * '''장점''' | ||
: 블록단위 암호화로 인해 기호를 삽입하거나 제거가 불가능하고 다양한 운영 방법에 의해 혼돈과 확산의 이론을 기반으로 설계될 수 있는 것이 장점이다. | : 블록단위 암호화로 인해 기호를 삽입하거나 제거가 불가능하고 다양한 운영 방법에 의해 혼돈과 확산의 이론을 기반으로 설계될 수 있는 것이 장점이다. | ||
| 13번째 줄: | 21번째 줄: | ||
<div class="mw-collapsible"> | <div class="mw-collapsible"> | ||
| − | ===암/복호화=== | + | ====암/복호화==== |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
[[파일:대칭 블록암호 암호화 복호화.png|600픽셀|가운데|]] | [[파일:대칭 블록암호 암호화 복호화.png|600픽셀|가운데|]] | ||
2019년 10월 25일 (금) 15:00 판
블록암호(block cipher)란 기밀성있는 정보를 정해진 블록 단위로 암호화하는 대칭키 암호시스템이다. 만약 암호화하려는 정보가 블록의 길이보다 길 경우에는 특정한 운용모드가 사용된다.(예 : ECB, CBC, OFB, CFB, CTR)
목차
특징
패딩
주어진 평문을 블록 암호로 암호화하기 위해서는 평문을 우선 블록 크기의 배수로 만들어야 합니다. 예를 들어 DES로 암호화를 한다면 평문은 비트이어야 한다. 평문의 길이가 블록 크기의 배수가 아닌 경우, 블록 크기의 배수가 되게끔 패딩을 추가한다. 이러한 패딩을 하는 알고리즘은 PKCS#5, ANSIX923 등이 존재한다.
패딩의 가장 중요한 원칙은 으로부터 M 을 복구할 수 있어야 한다는 점입니다. 이 원칙이 지켜지지 않으면 패딩된 메시지로부터 원본 메시지를 찾을 수 없습니다. 예를 들어 평문의 길이를 32비트의 배수로 만들고 싶을 때 모자란 만큼 0으로 채워 32의 배수로 만드는 패딩을 생각해봅시다. 그러면 패딩된 메시지 00010011 01000111 11001000 00000000에서 실제 평문이 어디까지인지 알 수 있을까요? 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있습니다. 즉 비트 단위의 All zero 패딩은 패딩된 메시지로부터 원본 메시지를 복구할 수 없으므로 사용할 수 없는 패딩입니다.
대칭키
구조
장단점
- 장점
- 블록단위 암호화로 인해 기호를 삽입하거나 제거가 불가능하고 다양한 운영 방법에 의해 혼돈과 확산의 이론을 기반으로 설계될 수 있는 것이 장점이다.
- 단점
- 블록 단위로 암호화가 이루어지기 때문에 평문 비트들이 완전한 하나의 블록으로 구성한 다음에 암호화 되므로 암호화 과정이 블록의 크기에 따라 지연된다. 즉, 암호화 시간이 느리다.
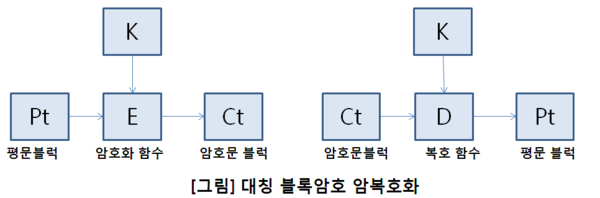
그림에서 t는 t번째를 의미한다. 즉, 일정 비트가 되어 블록이 되면 키와 암호화 함수를 이용하여 암호문 블록이 생성된다. 그리고 생성된 암호화 블록을 전송하고 이를 받은 측에서는 암호문 블럭을 다시 키와 복호 함수를 사용하여 평문 블록으로 만든다. Ct와 Pt 사이의 관계는 각각 Ct=E(Pt,K)와 Pt=D(Ct,K)이다. 왼쪽이 암호화가 이루어지는 과정이고 오른쪽이 복호화가 이루어지는 과정이며, 암호화와 복호화에 사용되는 열쇠는 K로 같다.
- 블록의 길이
- 블록의 길이(Pt)는 대표적으로 64비트와 128비트가 있다. 블록의 길이는 변수에 의해 지정 가능하고, 블록의 길이를 변경할 수 있는 것도 있다.
- K
- 키(Key)의 길이는 40, 56, 64, 80, 128, 192, 256비트가 있다.
- 안정성
- 블록 암호는 N비트의 키 길이에 대해 2 이상의 안정성을 가지지 않는다. 즉, 키의 전수 검색으로 반드시 해독할 수 있다. 이것은 블록암호를 정하는 경우, 매우 중요한 요소이다. 그래서 최근 짧은 키의 길이를 가진 DES(56비트)가 채용되지 않는다.
- 라운드 함수의 구성 방법에 따라 분류
- 파이스텔(Feistel) : DES, 3DES
- SPN : AES
- 비트별 블록 암호 종류
[1]64비트 - TDEA-ISO/IEC_18033, CRYPTREC
- MISTY1-ISO/IEC_18033, CRYPTREC, NESSIE
- CAST-128-ISO/IEC_18033
- CIPHERUNICORN-E – CRYPTREC
- Hierocrypt-L1 –CRYPTREC
- MULTI2-ARIB한정 수신 방식
- KASUMI
128비트 AES - Camellia
SEED - CIPHERUNICORN-A-CRYPTREC
- Hierocrypt-3-CRYPTREC
- SC2000 – CRYPTREC
256비트 - SHACAL-2-NESSIE
종류
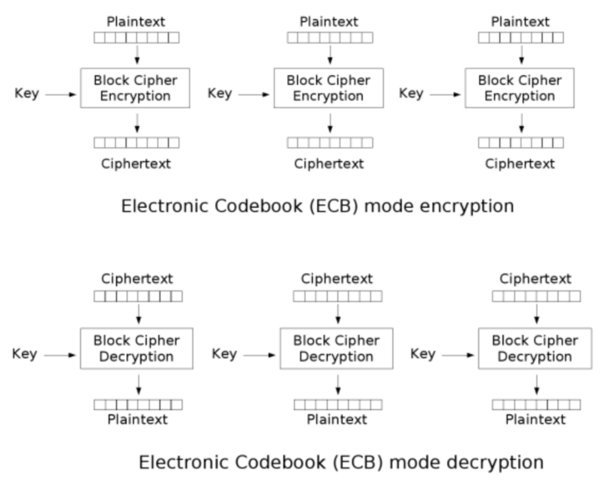
전자 코드북
전자 코드북(Electronic Codebook; ECB)은 운용 방식 중 가장 간단한 구조를 가지며, 암호화하려는 메시지를 여러 블록으로 나누어 각각 암호화하는 방식으로 되어있다. 전자 코드북은 모든 블록이 같은 암호화 키를 사용하기 때문에 보안에 취약하다. 만약 암호화 메시지를 여러 부분으로 나누었을 때, 두 블록이 같은 값을 가진다면, 암호화한 결과 역시 같다. 이것은 공격자가 비슷한 메시지를 반복적으로 암호화하는 반복공격에도 취약한 성질을 가진다.
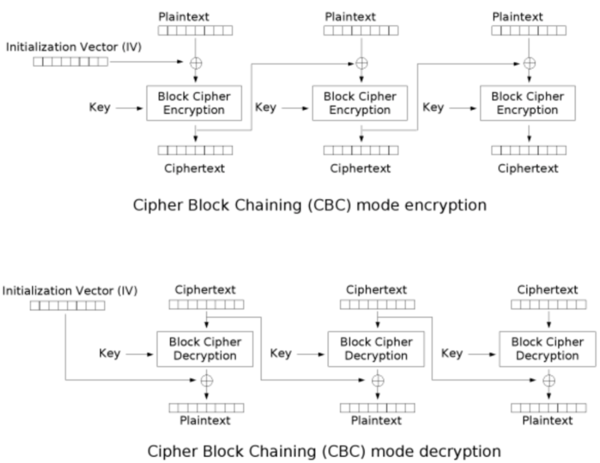
암호 블록체인
암호 블록체인(Cipher Block Chaining; CBC)방식은 1976년 IBM에 의해 개발되었다. 각 블록은 암호화되기 전에 이전 블록의 암호화 결과와 베타적 논리합(XOR)이 되며, 첫 블록의 경우에는 초기화 벡터가 사용된다. 초기화 벡터가 같은 경우 출력 결과가 항상 같기 때문에, 매 암호화마다 다른 초기화 벡터를 사용해야 한다. 암호 블록체인 방식은 현재 널리 사용되는 운용 방식 중 하나이다. 암호 블록체인은 암호화 입력 값이 이전 결과에 의존하기 때문에 병렬화가 불가능하지만, 복호화의 경우 각 블록을 복호화한 다음 이전 암호화 블록과 베타적 논리합을 하여 복구할 수 있기 때문에 병렬화할 수 있다.
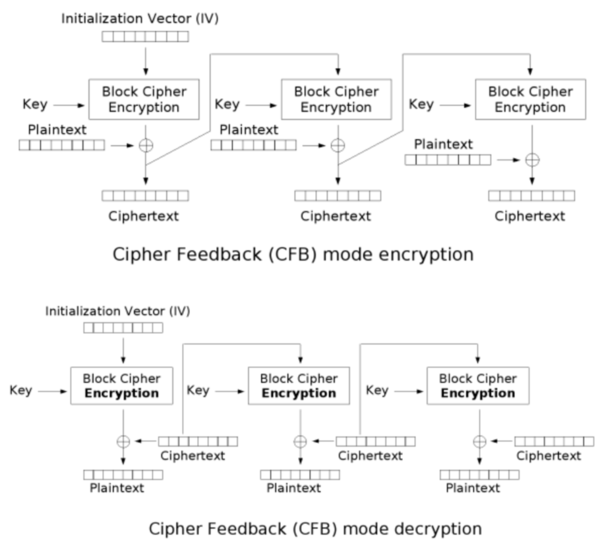
암호 피드백
암호 피드백(Ciper Feedback; CFB) 방식은 암호 블록체인의 변형으로, 블록 암호를 자기 동기 스트림 암호로 변환한다. 암호 피드백의 동작 방식은 암호 블록체인과 비슷하며, 특히 암호 피드백 암호 해제 방식은 암호 블록체인 암호화의 역순과 거의 비슷하다.
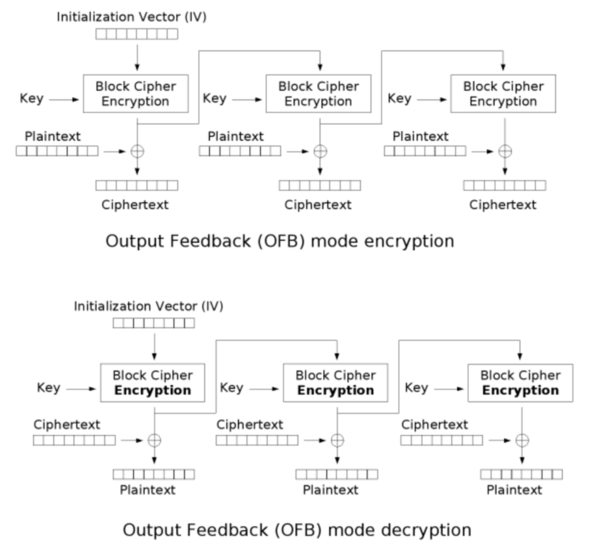
출력 피드백
출력 피드백(Output Feedback; OFB)은 블록암호를 동기식 스트림 암호로 변환한다. XOR 명령의 대칭 때문에 암호화의 암호 해제 방식은 완전히 동일하다.
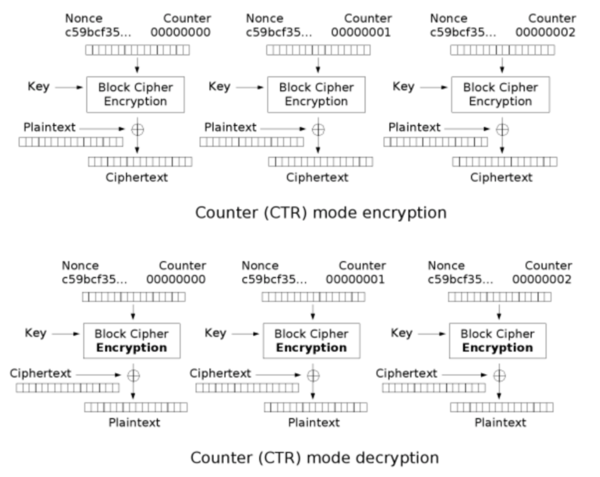
카운터
카운터(Counter; CTR) 방식은 블록암호를 스트림 암호로 바꾸는 구조를 가진다. 카운터 방식에서는 각 블록마다 현재 블록이 몇 번째인지 값을 얻어, 그 숫자와 논스를 결합하여 블록암호의 입력으로 사용한다. 그렇게 각 블록 암호에서 연속적인 난수를 얻은 다음 암호화하려는 문자열과 XOR한다. 카운터 모드는 각 블록의 암호화 및 복호화가 이전 블록에 의존하지 않아서 병렬적으로 동작하는 것이 가능하다. 혹은 암호화된 문자열에서 원하는 부분만 복호화하는 것도 가능하다.
각주
- ↑ Mark&People, 〈블럭 암호 방식에 대해 이해하기(대칭키)〉, 《티스토리》, 2011-12-27
- ↑ 불곰, 〈블록 암호 운용 방식 (block cipher modes of operation〉, 《티스토리》, 2017-02-18
참고자료
- 불곰, 〈블록 암호 운용 방식 (block cipher modes of operation〉, 《티스토리》, 2017-02-18
같이 보기

 위키원
위키원