"부정논리곱"의 두 판 사이의 차이
잔글 (→같이 보기) |
잔글 (→특징) |
||
| (같은 사용자의 중간 판 하나는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''부정논리곱'''(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. '''NAND'''라고도 한다. | + | '''부정논리곱'''(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. '''NAND'''(낸드)라고도 한다. |
| + | |||
== 개요 == | == 개요 == | ||
Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다. | Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다. | ||
| 58번째 줄: | 59번째 줄: | ||
초기의 집적 회로(표준 논리 IC)는 부품이 고가였기 때문에 가장 회로 구성이 간단한 NAND를 이용하여 다양한 논리 회로를 설계하였다. | 초기의 집적 회로(표준 논리 IC)는 부품이 고가였기 때문에 가장 회로 구성이 간단한 NAND를 이용하여 다양한 논리 회로를 설계하였다. | ||
| − | + | ; 부정논리곱(NAND)의 논리 기호의 표현과 이용되는 IC칩 | |
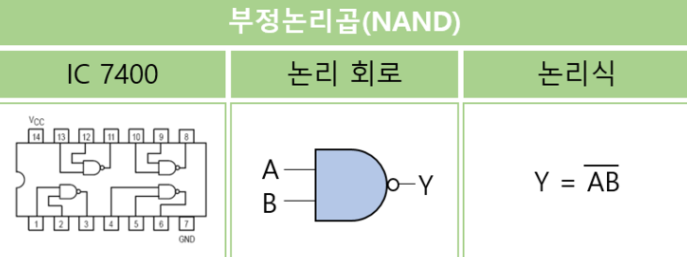
[[파일:부정논리곱(IC칩).png|썸네일|800픽셀|가운데|부정논리곱 논리회로]] | [[파일:부정논리곱(IC칩).png|썸네일|800픽셀|가운데|부정논리곱 논리회로]] | ||
대표적인 NAND 게이트 IC의 TTL는 74LS00(2입력), 74LS10(3입력), 74LS20(4입력)이 있고, CMOS는 CD4011(2입력), CD4023(3입력), CD4012(4입력)가 있다. | 대표적인 NAND 게이트 IC의 TTL는 74LS00(2입력), 74LS10(3입력), 74LS20(4입력)이 있고, CMOS는 CD4011(2입력), CD4023(3입력), CD4012(4입력)가 있다. | ||
| 75번째 줄: | 76번째 줄: | ||
{{암호 알고리즘|검토 필요}} | {{암호 알고리즘|검토 필요}} | ||
| − | |||
2020년 1월 6일 (월) 23:40 기준 최신판
부정논리곱(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. NAND(낸드)라고도 한다.
개요[편집]
Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다.
NAND 연산 결과 입력값 반환값 0, 0 1 0, 1 1 1, 0 1 1, 1 0
특징[편집]
일반적으로 NAND는 다음과 같이 정의된다.
A NAND B = NOT (A AND B)
진리표[편집]
명제 P 명제 Q P NAND Q 참 참 거짓 참 거짓 참 거짓 참 참 거짓 거짓 참
응용[편집]
일반적으로 논리 연산은 논리곱(AND), 논리합(OR), 논리부정(NOT)의 구성으로 표현 가능하다. 하지만, NAND는 모든 논리 연산을 표현할 수 있다. AND, OR, NOT 역시 NAND로 표현할 수 있다.
- NOT A = A NAND A
- A AND B = NOT ( A NAND B ) = ( A NAND B ) NAND ( A NAND B )
- A OR B = ( NOT A ) NAND ( NOT B ) = ( A NAND A ) NAND ( B NAND B )
초기의 집적 회로(표준 논리 IC)는 부품이 고가였기 때문에 가장 회로 구성이 간단한 NAND를 이용하여 다양한 논리 회로를 설계하였다.
- 부정논리곱(NAND)의 논리 기호의 표현과 이용되는 IC칩
대표적인 NAND 게이트 IC의 TTL는 74LS00(2입력), 74LS10(3입력), 74LS20(4입력)이 있고, CMOS는 CD4011(2입력), CD4023(3입력), CD4012(4입력)가 있다.
참고자료[편집]
- 〈논리 연산〉, 《나무위키》
- 〈부정논리곱)〉, 《위키백과》
- 〈불 대수의 기본 연산과 논리게이트(2)〉, 《네이버 블로그》
같이 보기[편집]

 위키원
위키원