|
|
| 7번째 줄: |
7번째 줄: |
| | * '''level''': 트리의 특정 깊이를 가지는 노드의 집합 | | * '''level''': 트리의 특정 깊이를 가지는 노드의 집합 |
| | * '''degree(차수)''': 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수 | | * '''degree(차수)''': 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수 |
| − | * '''Terminal Node''' ( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드 | + | * '''Terminal Node'''( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드 |
| − | * '''Internal Node''' (내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.<ref name='tree'></ref> | + | * '''Internal Node'''(내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.<ref name='tree'></ref> |
| | | | |
| | == 이진 트리(Binary Tree) == | | == 이진 트리(Binary Tree) == |
2020년 8월 12일 (수) 09:10 판
트리(tree)는 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조이다. 데이터 요소들의 단순한 나열이 아닌 부모-자식 관계의 계층적 구조로 표현이 된다.
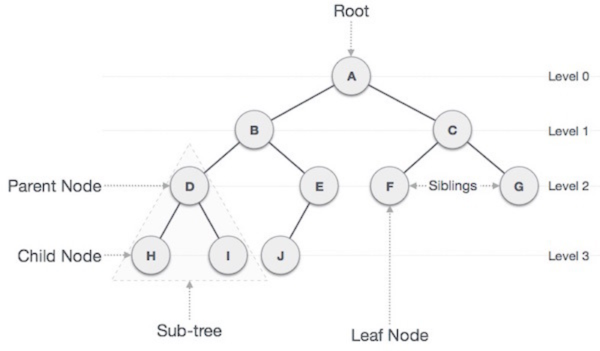
구조
 [1]
[1]
- node: 트리를 구성하고 있는 각 요소
- Edge(간선): 트리를 구성하기 위해 노드와 노드를 연결하는 선
- Root Node: 최상위 계층에 존재하는 노드
- level: 트리의 특정 깊이를 가지는 노드의 집합
- degree(차수): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- Terminal Node( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드
- Internal Node(내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.[1]
이진 트리(Binary Tree)
- 이진 트리(Binary Tree) : 이진트리는 트리를 구성하는 노드들의 최대 차수(degree)가 2인 노드들로 구성되는 트리이다.
- 이진트리의 레벨 i에서 가질 수 있는 최대 노드의 수는 2^i이다. (i>=0)
- 깊이가 k인 이진트리가 가질 수 있는 최대 노드의 수는 2^k-1이다.(k>=1)
- 이진트리는 완전 이진 트리(Completable Binary Tree)와 포화 이진 트리(Perfect Binary Tree), 전 이진 트리(Full Binary Tree)라고 하는 특별한 트리 구조를 정의할 수 있다.[1]
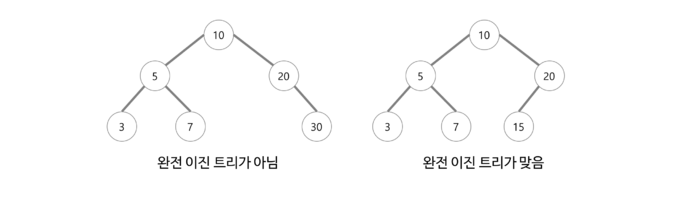
완전 이진 트리(Completable Binary Tree)
 [1]
[1]
- 트리를 구성하고 있는 임의의 두 단말 노드의 레벨 차이가 1 이하이고 마지막 레벨을 제외한 모든 레벨에 존재할 수 있는 모든 노드를 갖고 있으며, 왼쪽에서 오른쪽으로 채워지는 이진트리이다.
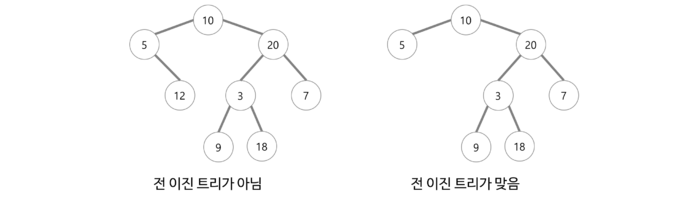
전 이진 트리(Full Binary Tree)
 [1]
[1]
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.
포화 이진 트리(Perfect Binary Tree)
- 모든 레벨에 노드가 차있는 상태로 최대 노드 수인 2^k-1개로 채워져 있는 트리이다.
- 전 이진 트리이면서 완전 이진 트리인 경우이다.[1]
같이 보기
|
 이 트리 문서는 데이터에 관한 토막글입니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 이 문서의 내용을 채워주세요. 이 트리 문서는 데이터에 관한 토막글입니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 이 문서의 내용을 채워주세요.
|
| 개발 : 프로그래밍, 소프트웨어, 데이터 □■⊕, 솔루션, 보안, 하드웨어, 컴퓨터, 사무자동화, 인터넷, 모바일, 사물인터넷, 게임, 메타버스, 디자인
|
|
|
| 데이터
|
ACID • CRUD • CSV • DAO • DB • DBMS • DB 명령어 • DCL • DDL • DML • DTO • ERD • ETL • JDBC • LOD • MDM • ODBC • RDBMS • RDF • SQL • 가상 데이터베이스 • 관계형 데이터베이스 • 그래프 • 기본키(PK) • 내부조인 • 널 • 노드 • 다이어그램 • 대리키 • 대체키 • 데이터 • 데이터댐 • 데이터마트 • 데이터 모델링 • 데이터뱅크 • 데이터베이스(DB) • 데이터베이스 언어 • 데이터 사이언스 • 데이터 사전 • 데이터 웨어하우스 • 데이터 정의어(DDL) • 데이터 제어어(DCL) • 데이터 조작어(DML) • 데이터 클러스터 • 데이터 토큰 (문자열) • 데이터 통합 • 덱 • 디비서버 • 라이트조인 • 락 • 레코드 • 레프트조인 • 로그 • 로그파일 • 로깅 • 롤백 • 리두로그 • 릴레이션 • 마스터데이터 • 마스터데이터관리(MDM) • 마이그레이션 • 메타데이터 • 배열 • 뷰 • 빅데이터 • 서브쿼리 • 수퍼키 • 순차리스트 • 스키마 • 스택 • 슬로우쿼리 • 엔티티 • 역정규화 • 연결리스트 • 외래키(FK) • 외부조인 • 인덱스 • 인덱싱 • 인젝션 • 자료구조 • 정규화 • 정보 • 조인 • 커밋 • 쿼리 • 큐 • 키 • 타깃 • 테이블 • 튜플 • 트랜잭션 • 트리 • 트리거 • 티비마이그레이터 • 풀조인 • 프로시저 • 필드 • 해시 • 해시맵 • 해시태그 • 해시테이블 • 해시함수 • 해싱 • 후보키
|
|
|
데이터베이스
관리 시스템
(DBMS)
|
관계형 데이터베이스 관리 시스템(RDBMS) • 노에스큐엘(NoSQL) • 데이터베이스 관리 시스템(DBMS) • 더비 • 디비투(DB2) • 레디스 • 마리아디비(MariaDB) • 마이에스큐엘(MySQL) • 몽고디비 • 빅테이블 • 사이베이스 • 선디비 • 알티베이스 • 액세스 • 에스큐엘(SQL) • 에스큐엘라이트(SQLite) • 에이치베이스 • 엠에스에스큐엘(MS-SQL) • 오라클(Oracle) • 인터베이스 • 인포믹스 • 카산드라 • 카우치디비 • 큐브리드 • 티베로 • 파이어버드 • 포스트그레스큐엘(PostgreSQL) • 하이퍼테이블
|
|
|
| DB 명령어
|
alter • array • create • delete • drop • from • full join • grant • inner join • insert • join • left join • null • order by • outer join • rename • revoke • right join • select • truncate • update • where
|
|
|
| 시스템 연계
|
API • CGI • EAI • ESB • JPA • RSS • SOA • SOAP • SSL • SSO • web3.js • XML • 디비투디비(DB-to-DB) • 레스트풀(RESTful) • 상호운용성 • 시스템 인터페이스 • 신디케이션 API • 오픈 API • 웹 API • 웹개방성 • 윈도우 API • 자바 API • 크롤링 • 프라이빗 API
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|

 위키원
위키원








