"타원곡선"의 두 판 사이의 차이
(→개요) |
|||
| (사용자 3명의 중간 판 94개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''타원곡선'''(elliptic curve)은 | + | '''타원곡선'''(elliptic curve)은 <math> y^{2}=x^{3}+ax+b </math> 형태의 [[방정식]]으로 나타나는 곡선으로서, <ref>〈[http://a.to/19cbFsi 타원 곡선 [楕圓曲線]]〉,《다음 한국어사전》 </ref> 첨 점이나 교차점 등의 특이점이 없는 것으로 중근을 갖지 않는 임의의 3차 혹은 4차 다항식 P에 대해 y2 = P(x)는 곡면 종수 1의 비특이 평면 곡선의 방정식이며, 보다 일반적으로는 종수가 1인 임의의 비특이 대수 곡선을 타원 곡선이라 한다. |
== 개요 == | == 개요 == | ||
| − | 타원곡선은 타원하고 별로 상관이 없고, 형태상으로는 | + | 타원곡선은 19세기 타원 함수론과 함께 발전하였으나 타원하고 별로 상관이 없고, 형태상으로는 [[타원]] 보다는 중괄호에 가까운 모양으로서 '타원곡선'이란 이름이 붙은 이유는 타원의 둘레를 구하기 위한 적분에서 유래했던 역사적 이유지만, 현재는 그것과 전혀 상관없이 사용되고 있으며, 항목이 등재된 이유는 이름이 혼란스러워서인 것은 아니고, 수학 전반에서 엄청난 중요성을 갖고 있기 때문이다. 같은 대상을 실 해석학에서, 복소 해석학에서, 대수 기하학에서, 정수론에서 모두 이야기할 수 있는 경우는 그렇게 많지 않다. 보통 y 좌표가 무한대라는 설정인 특이 점을 추가하는데, 이 특이 점은 매우 중요하다. 번외로 타원곡선에 대한 Birch and Swinnerton-Dyer 추측은 클레이 연구소가 선정한 7개의 밀레니엄 문제 중 하나이다. 이산 대수 문제를 타원곡선으로 옮겨 기밀성과 효율성을 높인 방식. 서명을 위해서는 [[ECDSA]](Elliptic Curve Digital Signature Algorithm) 를, 키 교환을 위해서는 [[ECDH]](Elliptic curve Daffie? Hellman)를 사용한다.<ref>한국정보통신 기술협회 공식홈페이지 -https://www.tta.or.kr </ref> |
== 정의 == | == 정의 == | ||
| − | + | 실수 위에서의 타원곡선은 a와 b가 고정된 실수일 경우에 방정식 <math> y^{2}=x^{3}+ax+b </math> 을 만족하는 (x, y)점들의 집합을 의미한다. 우변인 x3+ax+b가 중근을 갖지 않으면, 즉 4a3+27b2 ≠ 0 이면타원곡선은 군을 정의 할 수 있는 대수적 특성을 제공하는 것이다. 원점이 주어진 [[대수곡선]] 이란 순서쌍 <math> (M,x_{0}) x_{0}\in M, {\displaystyle M} </math> M은 대수곡선)을 의미한다. 임의의 체의 표수에서, 타원곡선은 일반적으로 다음과 같은 같은 꼴의 식의 해의 집합으로 나타낼 수 있다. | |
| + | # 타원곡선은 특이점을 가지지 않는다. | ||
| + | # 타원곡선은 복소수체의 경우 위상수학적으로 원환면곡면 으로 종수가 1이다. | ||
| + | # 대수 곡선을 정의하는 식을 만족시키는 점 <math> (x,y)\in k^{2} </math>적어도 하나 존재하여 점은 무한대에 있을 수도 있으며, 적어도 하나의 유리점을 가진다. | ||
| + | : <math> y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}</math> 만약 체의 표수가 2나 3이 아닌 경우, 타원곡선은 다음과 같은 꼴의 식의 해의 집합으로 나타낼 수 있다.<math> y^{2}=x^{3}-px-q </math> 여기서(1, x, y) (1, x, y)는 사영 평면의 동차좌표이고, 원점은(0, 0, 1) (0, 0, 1)이 된다. 이 점은(x, y) (x, y) 평면에서의 무한대에 해당하며, (x, y) (x, y) 평면에 무한대를 추가하여 사영 평면을 취한 뒤, 타원곡선을 사영 평면 속의 곡선으로 간주한다. 체의 표수가 3인 경우, 일반적인 타원곡선은 다음과 같은 꼴의 식의 해의 집합으로 나타낼 수 있어 y^{2}=4x^{3}+b_{2} x^{2}+2b_{4} x+b_{6} 체의 표수가 2인 경우는 위의 일반적인 표현을 사용하여야 한다. <ref name="백">〈[http://a.to/19kmXo2 타원곡선]〉, 《위키백과》 </ref> | ||
| + | |||
| + | == 역사 == | ||
| + | : 타원 적분(elliptic integral)에서 그 이름을 땄다. 이름과는 달리, 타원과 직접적인 관련이 없으며, 타원은 2차 곡선이므로, 곡선으로서 타원 곡선(3차 곡선)이 아니다. 현재 타원곡선으로 불리는 대상은 디오판토스가 최초로 이고, 디오판토스는 y(a-y)=x^{3}-x 꼴의 타원곡선에 대하여 기술하였다. 피에르 드 페르마와 아이작 뉴턴, 카를 구스타프 야코프 야코비, 카를 바이어슈트라스, 앙리 푸앵카레 등이 타원곡선에 대하여 연구하였으며, 존 테이트 등이 타원곡선 이론을 수론과 연관 지었다. 앤드루 와일스는 타원곡선에 대한 [[모듈러 성]] 정리(의 상당 부분)를 증명하여, 이를 통해 [[페르마]] 의 마지막 정리를 증명하여 [[유한체]] 에 대한 타원곡선은 엄호론에서 타원곡선 암호를 정의하는 데 사용한다. | ||
== 특징 == | == 특징 == | ||
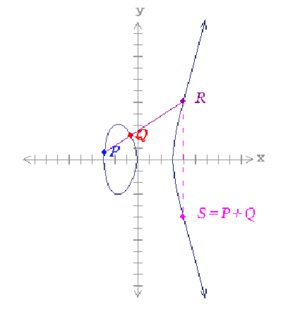
| − | [[파일:그림1.PNG|썸네일|300픽셀|'''그림 1. 타원곡선''' | + | [[파일:그림1.PNG|썸네일|300픽셀|'''그림 1. 타원곡선''' y<sup>2</sup>=x<sup>3</sup>-9x-1와 타원곡선 위의 덧셈]] |
| − | * 그림 1은 | + | * 그림 1은 y<sup>2</sup>=x<sup>3</sup>-9x-1인 타원곡선이다. 실수 위에서의 타원곡선 군은 해당 타원곡선 위의 모든 점들과 무한대 점이라고 명명된 특수 점으로 구성되고 여기에 덧셈이 정의된다. 점 P(x1 , y1)와 점 Q(x2, y2)를 더하기 위해서 P와 Q를 잇는 선을 그으면 타원곡선 위의 다른 점 R과 교차한다. 만약 P=Q이면 점 P에 대한 접선을 그으면 된다. 계산한 점 R을 X축에 대칭을 시킨 다른 점 S가 P+Q로 정의된다. 점 P와 점 Q의 합을 구하는 방법은 다른 교점 R의 X축 대칭이고, ( 기하학적 연산 )점 P와 상수 N의 곱은 점과 점의 합을 여러 번 반복한다. <ref>우주를줄게, 〈[https://tokenbank.co.kr/news/detail/28155/ 타원곡선 암호과 이더리움 전자서명]〉, 《티스토리》 </ref> |
| + | |||
| + | * '''군 (Group)''' | ||
| + | : 군은 하나의 이항 연산자에 대해서 특수한 조건을 가진 수의 집합으로 모든 정수는 덧셈에 대해서 군을 이룬다. 정수를 정수와 더하면 정수가 나올 것이고 더샘은 결합법칙이 성립하는 연산으로 정수 안에는 더샘의 항등원인 0이 있고, 역원인 음수가 있다. 예를 들면 42의 역원은 -42이고 항등원은 0이라면, 모든 정수가 덧셈에 대해서 군을 이룬다. 정수와 같이 덧셈에 대한 군을 덧셈 군이라 부르고, 곱셈에 대해서 군이 성립하면 곱셈 군이다. <ref>Luavis, 〈[https://b.luavis.kr/science/elliptic-curve 타원곡선 디피 헬만]〉,《생계코딩 이야기》, 2019-02-17 </ref> 요약하면 군은 정의된 [[연산자]]에 대해서 닫혀있어야 하고, 연산자에 대해서 결합법칙이 성립되어야 하며, 군 안에는 항등원과 역원이 있어야 한다. 군은 역원이 없으며, 2의 곱셈에 대한 역원은 1/2인데 이는 정수가 아닌 [[유리수]] 라고 하면 유리수에는 0이 있는데, 0은 곱셈에 대한 역원이 존재하지 않는다.(1/0은 계산할 수 없다)따라서 0을 제외한 유리수가 곱셈군을 이룬다. 또는 모든 타원곡선에는 다음과 같은 두 점을 더하는 매우 신기한 연산이 있다. 두 점 P = (x1 , y1)와 Q = (x2 , y2) 가 있다고 할 때, 이들의 합 P+Q는 이렇다. | ||
| + | # P와 Q를 잇는 직선 l은 타원곡선과 다른 한 점 R = (x3 , -y3)에서 만난다. | ||
| + | # R을 x축에 대칭시킨 S = (x3 , y3)가 P+Q가 된다. | ||
| + | # 예외규칙 으로 무한점 ∞에 대해서는 "∞을 지나는 직선은 y축과 평행한 직선이다" 라는 규칙을 적용시키는데 l이 y축에 평행해서 다른 일반 점하고 안 만날 때는, R은 ∞로 정의 하고, P=∞일 때는, l은 'Q를 지나고 y축에 평행한 직선'이 된다. | ||
| + | # 예외규칙 으로 l이 다른 한 점 R에서 만나지 않을 경우에는, l은 P 또는 Q에서 접할 것이고 이 때 R은 l이 접하는 점이 된다. | ||
| + | # 예외규칙 으로 P=Q인 경우에는 l은 'P에서 그은 접선'으로 정의 하는데 l이 다른 한 점 R에서 만나지 않는다면 l은 P에서 변곡점을 가져야 하며, 이 때 R은 P로 생각한다. | ||
| + | # 예외규칙 으로 ∞에서 그은 접선은 ∞에서 변곡점을 가진다. ∞를 x축에 대칭시키면 ∞이다. | ||
* '''타원곡선 군에서의 덧셈의 특성''' | * '''타원곡선 군에서의 덧셈의 특성''' | ||
| − | # 무한대 점은 O로 표기하며 타원곡선 위의 임의의 점 P에 대해서 P+O=P가 | + | # 무한대 점은 O로 표기하며 타원곡선 위의 임의의 점 P에 대해서 P+O=P가 성립되며, [[무한대]] 점은 덧셈 상의 항등원이 된다. |
| − | # 타원곡선 위의 임의의 점 P에 대해서 P+Q=O를 만족하는 점 Q가 존재하는데 Q=-P로 나타내며 뺄셈 R-S는 R+(-S)로 | + | # 타원곡선 위의 임의의 점 P에 대해서 P+Q=O를 만족하는 점 Q가 존재하는데 Q=-P로 나타내며 뺄셈 R-S는 R+(-S) 로 정의되고, 점 -P는 점 P의 X축의 대칭점이 되기 때문에 점 P의 좌표가 (x, y)이면 점 -P의 좌표는(x, -y) 이 된다. |
| − | # 타원곡선 위의 임의의 점 P, Q와 R에 대해서 P+(Q+R)=(P+Q)+R이 성립한다. 타원곡선 위의 임의의 점 P와 Q에 대해서 P+Q=Q+P가 | + | # 타원곡선 위의 임의의 점 P, Q와 R에 대해서 P+(Q+R)=(P+Q)+R이 성립한다. 타원곡선 위의 임의의 점 P와 Q에 대해서 P+Q=Q+P가 성립하므로 타원곡선 군은'가환군'이 된다. |
| + | |||
* ''' 타원곡선 위에서의 기하학적 연산''' | * ''' 타원곡선 위에서의 기하학적 연산''' | ||
| − | : 타원곡선 위에서의 기하학적 연산은 그대로 대수적인 연산으로도 | + | : 타원곡선 위에서의 기하학적 연산은 그대로 대수적인 연산으로도 설명이 된다. (x1, y1), (x2, y2), (x3, y3)'를 각각 점 P, Q, S=P+Q의 좌표라 한다면, 점 P+Q의 좌표(x3, y3)를 통해서 표현하고자 x1, x2, y1, y2 을 통해서 표현하고자 한다. R = (x3, y3)=-S가 성립되므로 y=α x+β를 점 P와 Q를 지나는 선의 방정식이다. 만약, (α x+β) 2 = x3+ax+b가 성립하면 점 P와 Q를 지나는 선 위의 점(x, α x+β)은 타원 곡선 위의 점이 되고, 3차 방정식 x3 - (α x+β) 2 + ax+b의 각각의 근에 대하여 한 개의 교차점이 존재하게 된다. (x1, αx1+β)'과 (x2, αx2+β)는 타원곡선 위의 두 점 P와 Q이기 때문에 이미 x1, x2가 근임을 알고 있다. 차수가 가장 높은 항의 계수가 1인 다항식에서 그 다항식에 존재하는 모든 근의 합은 차수 가두 번째로 높은 항의 계수에‘-’를 붙은 값과 동일하기 때문에 x1+ x2 + x3 = α2, 이 된다. 나머지 근은 x3 = α2 - x1 - x2와 y3 = αx3+β = y1 + α(x3 - x1)이 된다. P+Q에서 P=Q가 되며 는 점 P에서의 미분 값이 되기 때문에 음함수 미분을 하면 2yy'=3x2 / 2 y1 가 된다.<ref name="코">코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 </ref> |
| − | 만약, ( | ||
'''< 예제 >''' | '''< 예제 >''' | ||
| − | : y2 = x3-17x+16 에 의해서 정의되는 타원곡선 위의 두 점 P=(0, -4), Q=(1, 0) 이 주어졌을 때, P+Q는 다음과 같이 구할 수 있다. 즉, x1=0 , y1 =-4, x2 =1, y2 =0 | + | : y2 = x3-17x+16 에 의해서 정의되는 타원곡선 위의 두 점 P=(0, -4), Q=(1, 0) 이 주어졌을 때, P+Q는 다음과 같이 구할 수 있다. 즉, x1=0, y1 =-4, x2 =1, y2 =0 을식-1에 대입하면 을 얻게 되므로 P+Q=(15, -56) 이 된다. 실수 계산은 일반적으로 느리며 또한 반올림에 따른 오차로 인하여 정확하지가 않기 때문에 암호 응용에는 적합하지 않아서, [[암호 시스템]] 구축을 위해서는 유한체위에서 정의된 타원곡선 군이 이용된다. P가 소수일 때 유한체 GF(P) 상에서의 타원곡선은 a, b∈GF(P)의 경우에 방정식 y2 mod p =x3+ax+b mod p를 만족하는(x, y) 점들의 집합과 무한대 점 O를 의미하고 x, y∈GF(P)이며, 4a 3 + 27b ≠0 (mod p)이면 타원곡선 군이 정의된다.<ref name="코">코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 </ref> |
* '''타원곡선 이산대수 문제''' | * '''타원곡선 이산대수 문제''' | ||
| − | : 소수 p에 대해서 GF(p)를 p개의 원소로 구성된 유한체라 하면, 타원곡선 위의 점 P의 위수 t는 | + | : 소수 p에 대해서 GF(p)를 p개의 원소로 구성된 유한체라 하면, 타원곡선 위의 점 P의 위수 t는 TP=O를 만족하는 가장 작은 정수 t로 정의되고, GF(P) 상에서 정의된 타원곡선과 점 Q, 그리 고위수가 t인 타원곡선 위의 점 P가 주어졌을 때 Q=XP를 만족하는 정수 x∈[0, t-1]을 구하는 것을 타원곡선 이산대수 문제이다. 타원곡선 이산대수 문제의 가장 직접적인 해결방법은 Q를 구할 때까지 단순히 P, 2P=P+P, 3P=P+P+P, …를 연속적으로 계산하는 것이지만 t의 값이 매우 클 경우에는 실효성이 게 되어 현재까지 알려진 가장 효율적인 알고리즘은 Pollard의 rho 알고리즘 으로서 번의타원곡선 덧셈이 소요된다. Pohlig-Hellman알고리즘 역시 적용이 가능하지만, t가 소수일 경우에는 [[실효성]] 이 없어지게 되면, 대부분의 학자에 의해서 타원곡선 이산대수 문제는 소인수 분해나 이산대수 문제보다 훨씬 더 어려운 문제로 인식이 된다. 타원곡선 이산대수 문제에 대한 좀 더 적극적인 공격은 Pollard의 rho 알고리즘에 기반을 두고 병렬처리를 가능하게 하는 특수목적의 하드웨어를 구축하는 것이다. 하지만 이런 공격도 t2160 인 경우에는 불가능하게 된다. 현재 타원곡선 암호에 적용 가능한 타원곡선 이산대수의 t 값은 단기적으로 150bit, 장기적으로 180bit 이상이 권고된다.<ref name="코">코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 </ref> |
| + | |||
| + | [[파일:K9.PNG|썸네일|400픽셀|'''실수체상의 타원곡선 그래프''']] | ||
| + | |||
| + | === 체에대한 타원곡선 === | ||
| + | |||
| + | * '''실수체 위의 타원곡선''' | ||
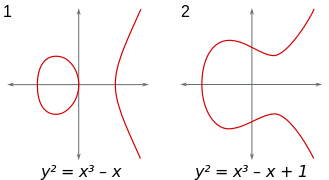
| + | : 실수 체 상에서, 타원곡선은 실수 a와 b에 대해 방정식 y2 = x3 + ax + b로 정의되는 평면 곡선으로 1이 아닌 3차 항의 계수와 0이 아닌 2차 항의 계수는 x, y를 다시 정의함으로써 흡수시킬 수 있기에 우변이 임의의 x의 3차식이면 언제나 이런 형태의 식을 바이어슈트라스 방정식으로 만들 수 있다. 타원곡선의 정의에는 이 곡선이 비특이 하다는 조건이 포함되고, 기하학적으로 말하자면 이는 곡선의 그래프가 첨 점이나 교차점이 없다는 뜻으로 판별식 Δ = −16(4a 3 + 27b 2)이 0이 아니라는 대수적인 조건과 동치이다. 비특이 대수 곡선은 판별식이 양수일 경우 두 개의 연결 성분을 가지고, 음수일 경우에는 하나의 연결 성분만을 가진다. 옆의 그래프에서 첫 번째 곡선의 판별식은 64, 두 번째 곡선의 판별식은 −368이다. | ||
| + | |||
| + | * '''복소수체 위의 타원곡선''' | ||
| + | : 복소수체에서의 타원곡선은 1차원 아벨 다양체이다. 종수가 1이므로, 기하학적으로 이는 원환면의 모양을 하고 있다. 임의의 타원곡선<math> y^{2}=4x^{3}-px-q</math>가 주어졌다면, 원환면으로 여길 수 있으며, 복소 구조를 갖춘 원환면은 격자<math> \Lambda \subset {\mathbb C}</math>에 대한 몫공간 <math> {\mathbb C}/\Lambda </math> 로 여길 수 있다. 그렇다면 이 원환면에서 타원곡선으로 바이어슈트라스 타원함수<math> \wp (z;\Lambda ) </math>를 사용해 다음과 같은 사상을 정의할 수 있다. | ||
| + | : <math>z\in {\mathbb C}/\Lambda </math> | ||
| + | : <math>z\mapsto (x,y)=(\wp (z;\Lambda ),\wp '(z;\Lambda )) </math> | ||
| + | : 바이어슈트라스 타원함수는 다음과 같은 항등식을 만족시킨다. <math>\wp '(z;\Lambda )^{2}=4\wp (z;\Lambda )^{2}-g_{2}(\Lambda )\wp (z)-g_{3}(\Lambda ) </math> 따라서 이는 <math>(p,q)=(g_{2}(\Lambda ),g_{3}(\Lambda ))</math> 인 타원 곡선과의 동형사상이다. | ||
| + | |||
| + | * '''수체 위의 타원곡선''' | ||
| + | : 유리 수 체를 비롯한 다른 대수적 수 체에 대한 타원곡선은 수론에서 중요한 위치를 차지하는데 수 체에 대한 타원곡선의 점들은 보통 유리 점 이라 하고, 주어진 수 체 K에 대하여, 타원곡선 E의 K-유리 점들의 집합 E(K)는 아벨 군을 이룬다. 모델-베유 정리에 따라서, 타원곡선의 유리점군 E(K)는 항상 유한 생성 아벨 군이며, 따라서 그 계수와 꼬임 부분 군에 의해 주어진다. [[유리수체]] 의 경우, 유리 점 군의 꼬임 부분 군은 메이저 꼬임 정리에 따라 15가지의 가능한 군 가운데 하나이며, 다른 수 체의 경우에도 메이저 꼬임 정리와 유사한, 가능한 꼬임 부분군 목록들이 존재한다. | ||
| + | |||
| + | * '''유한체 위의 타원곡선''' | ||
| + | : 유한체 <math> \mathbb {F} _{q}</math>에 대한 타원곡선은 유한개의 점들로 이루어져 유한 군을 이루고 점의 개수를 세는 것은 일반적으로 매우 어려운 문제이며, 수론의 주요 연구 분야 가운데 하나이다. 하세 정리에 따라 <math> \mathbb {F} _{q}</math>위의 타원곡선 E에 대하여, 그 점의 수 <math> \#E({\mathbb F}_{q})</math>는 다음과 같은 상계 및 하계를 가진다. <math> q+1-2{\sqrt q}\leq \#E({\mathbb F}_{q})\leq q+1+2{\sqrt q}</math> 유한체에 대한 타원곡선의 점들이 이루는 유한군은 항상 두 순환군의 곱으로 유한체 <math> {\mathbb F}_{{71}}</math>에 대한 타원 곡선 <math> y^{2}=x^{3}-x</math>은 72개의 점 을 갖고, 그 군 구조는 2차 순환군과 36차 순환군의 곱이다. <math>({\mathbb Z}/2{\mathbb Z})\times ({\mathbb Z}/36{\mathbb Z})</math>유한체에 대한 타원곡선은 타원곡선 암호를 정의 하는데 사용한다. | ||
| + | |||
| + | === 공개키 암호 === | ||
* '''다른 공개키 암호와 비교''' | * '''다른 공개키 암호와 비교''' | ||
| − | : | + | : RSA 공개키 암호나 DSA 디지털 서명의 경우에 법 n과 p의 크기가 각각 1024bit 이상이 되고, 타원곡선 암호의 경우에는 160bit 이상이 요구되므로 타원곡선 암호의 경우에는 RSA나 DSA보다 짧은 키를 가지고도 높은 수준의 안전성이 보장되기 때문에 실제 구현에 있어서 안전성과 효율성이 모두 뛰어난 암호로 인식되고 있다.<ref name="코">코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 </ref> |
| − | + | :{|class=wikitable width=600 | |
| − | : < 타원곡선 이산대수와 소인수 분해에 | + | |+<big>'''< 타원곡선 이산대수와 소인수 분해에 드는 계산량 >'''</big> |
| − | + | !align=center|<math> p(bits) </math> | |
| + | !align=center|<math> t(bits) </math> | ||
| + | !align=center|<math>\sqrt{\pi(\frac{t}{2})}</math> | ||
| + | !align=center|mips-year | ||
| + | |- | ||
| + | |align=center|163 | ||
| + | |align=center|160 | ||
| + | |align=center|<math> 2^{80} </math> | ||
| + | |align=center|<math>9.6x10^{11}</math> | ||
| + | |- | ||
| + | |align=center|191 | ||
| + | |align=center|186 | ||
| + | |align=center|<math> 2^{93} </math> | ||
| + | |align=center|<math>7.9x10^{15}</math> | ||
| + | |- | ||
| + | |align=center|239 | ||
| + | |align=center|234 | ||
| + | |align=center|<math> 2^{117} </math> | ||
| + | |align=center|<math>1.6x10^{23}</math> | ||
| + | |- | ||
| + | |align=center|359 | ||
| + | |align=center|354 | ||
| + | |align=center|<math> 2^{177} </math> | ||
| + | |align=center|<math>1.5x10^{41}</math> | ||
| + | |- | ||
| + | |align=center|431 | ||
| + | |align=center|426 | ||
| + | |align=center|<math> 2^{213} </math> | ||
| + | |align=center|<math>1.0x10^{52}</math> | ||
| + | |} | ||
| + | :{|class=wikitable width=250 | ||
| + | |- | ||
| + | !align=center|<math> n(bits) </math> | ||
| + | !align=center|<math> mips-year </math> | ||
| + | |- | ||
| + | |align=center|512 | ||
| + | |align=center|<math>3*10^{4}</math> | ||
| + | |- | ||
| + | |align=center|768 | ||
| + | |align=center|<math>2*10^{8}</math> | ||
| + | |- | ||
| + | |align=center|1024 | ||
| + | |align=center|<math>3*10^{11}</math> | ||
| + | |- | ||
| + | |align=center|1280 | ||
| + | |align=center|<math>1*10^{14}</math> | ||
| + | |- | ||
| + | |align=center|1536 | ||
| + | |align=center|<math>3*10^{20}</math> | ||
| + | |} | ||
* '''타원곡선 공개키 암호''' | * '''타원곡선 공개키 암호''' | ||
| − | : 이산대수에 기반을 둔 | + | : 이산대수에 기반을 둔 공개키 암호는 타원곡선 이산대수에 기반을 둔 공개키 암호로 전환된다. 두 시스템에서의 암호화 및 복호화 그리고 공개키 및 개인키를비교하면, 타원곡선 공개키 암호에서는 공개키 G와 Y 그리고 평문 M과 암호문 C1과 C2는 모두 타원곡선 위의 점으로 두 시스템 간의 기본적인 차이점은 ? 공개키 암호에서의 지수 승과 곱셈 작업이 타원곡선 공개키 암호에서는 각각 배수와 덧셈 작업으로 전환된다.<ref name="코">코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 </ref> |
| − | + | :{|class=wikitable width=600 | |
| − | : < ElGamal 공개키 암호와 타원곡선 공개키 암호 비교 > | + | |+<big>'''< ElGamal 공개키 암호와 타원곡선 공개키 암호 비교 >'''</big> |
| + | !align=center| | ||
| + | !align=center|ELGamal 공개키 암호 | ||
| + | !align=center|타원곡선 공개키 암호 | ||
| + | |- | ||
| + | |align=center|공개키 | ||
| + | |align=center|<math>(g,py=g^{2}mod p)</math> | ||
| + | |align=center|<math>(G,p,Y=xG')</math> | ||
| + | |- | ||
| + | |align=center|개인키 | ||
| + | |align=center|<math>(x)</math> | ||
| + | |align=center|<math>(x)</math> | ||
| + | |- | ||
| + | |align=center|암호화 | ||
| + | |align=center|<math>(c_{1},c_{2})=(g^{%} mod p, y^{%}m mod p)</math> | ||
| + | |align=center|<math>(C_{1},C_{2})=(x'G,x'Y+M)</math> | ||
| + | |- | ||
| + | |align=center|복호화 | ||
| + | |align=center|<math>C_{1}, C_{2}^{%} mod p</math> | ||
| + | |align=center|<math>C_{2}-x_C{1}</math> | ||
| + | |} | ||
| 40번째 줄: | 146번째 줄: | ||
== 참고자료 == | == 참고자료 == | ||
| + | * 우용이, 〈[https://yygg9800.blog.me/221149160405 타원곡선]〉, 《네이버》, 2017-11-27 | ||
* 코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 | * 코원동서, 〈[http://a.to/19JtTQA 타원곡선 암호 시스템(공개키 암호)]〉 | ||
* 〈[http://a.to/19kmXo2 타원곡선]〉, 《위키백과》 | * 〈[http://a.to/19kmXo2 타원곡선]〉, 《위키백과》 | ||
| + | * 〈[http://a.to/19u2wX0 타원곡선]〉, 《나무위키》 | ||
| + | * Crocus, 〈[https://www.crocus.co.kr/1226 타원 곡선 암호학(Elliptic Curve Cryptography)]〉 | ||
| + | * 〈[https://wiki.mathnt.net/index.php?title=%ED%83%80%EC%9B%90%EA%B3%A1%EC%84%A0 타원곡선]〉, 《수학노트》 | ||
| + | * 우주를줄게, 〈[https://tokenbank.co.kr/news/detail/28155/ 타원곡선 암호과 이더리움 전자서명]〉, 《티스토리》 | ||
== 같이 보기 == | == 같이 보기 == | ||
2022년 9월 27일 (화) 15:58 기준 최신판
타원곡선(elliptic curve)은 형태의 방정식으로 나타나는 곡선으로서, [1] 첨 점이나 교차점 등의 특이점이 없는 것으로 중근을 갖지 않는 임의의 3차 혹은 4차 다항식 P에 대해 y2 = P(x)는 곡면 종수 1의 비특이 평면 곡선의 방정식이며, 보다 일반적으로는 종수가 1인 임의의 비특이 대수 곡선을 타원 곡선이라 한다.
개요[편집]
타원곡선은 19세기 타원 함수론과 함께 발전하였으나 타원하고 별로 상관이 없고, 형태상으로는 타원 보다는 중괄호에 가까운 모양으로서 '타원곡선'이란 이름이 붙은 이유는 타원의 둘레를 구하기 위한 적분에서 유래했던 역사적 이유지만, 현재는 그것과 전혀 상관없이 사용되고 있으며, 항목이 등재된 이유는 이름이 혼란스러워서인 것은 아니고, 수학 전반에서 엄청난 중요성을 갖고 있기 때문이다. 같은 대상을 실 해석학에서, 복소 해석학에서, 대수 기하학에서, 정수론에서 모두 이야기할 수 있는 경우는 그렇게 많지 않다. 보통 y 좌표가 무한대라는 설정인 특이 점을 추가하는데, 이 특이 점은 매우 중요하다. 번외로 타원곡선에 대한 Birch and Swinnerton-Dyer 추측은 클레이 연구소가 선정한 7개의 밀레니엄 문제 중 하나이다. 이산 대수 문제를 타원곡선으로 옮겨 기밀성과 효율성을 높인 방식. 서명을 위해서는 ECDSA(Elliptic Curve Digital Signature Algorithm) 를, 키 교환을 위해서는 ECDH(Elliptic curve Daffie? Hellman)를 사용한다.[2]
정의[편집]
실수 위에서의 타원곡선은 a와 b가 고정된 실수일 경우에 방정식 을 만족하는 (x, y)점들의 집합을 의미한다. 우변인 x3+ax+b가 중근을 갖지 않으면, 즉 4a3+27b2 ≠ 0 이면타원곡선은 군을 정의 할 수 있는 대수적 특성을 제공하는 것이다. 원점이 주어진 대수곡선 이란 순서쌍 M은 대수곡선)을 의미한다. 임의의 체의 표수에서, 타원곡선은 일반적으로 다음과 같은 같은 꼴의 식의 해의 집합으로 나타낼 수 있다.
- 타원곡선은 특이점을 가지지 않는다.
- 타원곡선은 복소수체의 경우 위상수학적으로 원환면곡면 으로 종수가 1이다.
- 대수 곡선을 정의하는 식을 만족시키는 점 적어도 하나 존재하여 점은 무한대에 있을 수도 있으며, 적어도 하나의 유리점을 가진다.
- 만약 체의 표수가 2나 3이 아닌 경우, 타원곡선은 다음과 같은 꼴의 식의 해의 집합으로 나타낼 수 있다. 여기서(1, x, y) (1, x, y)는 사영 평면의 동차좌표이고, 원점은(0, 0, 1) (0, 0, 1)이 된다. 이 점은(x, y) (x, y) 평면에서의 무한대에 해당하며, (x, y) (x, y) 평면에 무한대를 추가하여 사영 평면을 취한 뒤, 타원곡선을 사영 평면 속의 곡선으로 간주한다. 체의 표수가 3인 경우, 일반적인 타원곡선은 다음과 같은 꼴의 식의 해의 집합으로 나타낼 수 있어 y^{2}=4x^{3}+b_{2} x^{2}+2b_{4} x+b_{6} 체의 표수가 2인 경우는 위의 일반적인 표현을 사용하여야 한다. [3]
역사[편집]
- 타원 적분(elliptic integral)에서 그 이름을 땄다. 이름과는 달리, 타원과 직접적인 관련이 없으며, 타원은 2차 곡선이므로, 곡선으로서 타원 곡선(3차 곡선)이 아니다. 현재 타원곡선으로 불리는 대상은 디오판토스가 최초로 이고, 디오판토스는 y(a-y)=x^{3}-x 꼴의 타원곡선에 대하여 기술하였다. 피에르 드 페르마와 아이작 뉴턴, 카를 구스타프 야코프 야코비, 카를 바이어슈트라스, 앙리 푸앵카레 등이 타원곡선에 대하여 연구하였으며, 존 테이트 등이 타원곡선 이론을 수론과 연관 지었다. 앤드루 와일스는 타원곡선에 대한 모듈러 성 정리(의 상당 부분)를 증명하여, 이를 통해 페르마 의 마지막 정리를 증명하여 유한체 에 대한 타원곡선은 엄호론에서 타원곡선 암호를 정의하는 데 사용한다.
특징[편집]
- 그림 1은 y2=x3-9x-1인 타원곡선이다. 실수 위에서의 타원곡선 군은 해당 타원곡선 위의 모든 점들과 무한대 점이라고 명명된 특수 점으로 구성되고 여기에 덧셈이 정의된다. 점 P(x1 , y1)와 점 Q(x2, y2)를 더하기 위해서 P와 Q를 잇는 선을 그으면 타원곡선 위의 다른 점 R과 교차한다. 만약 P=Q이면 점 P에 대한 접선을 그으면 된다. 계산한 점 R을 X축에 대칭을 시킨 다른 점 S가 P+Q로 정의된다. 점 P와 점 Q의 합을 구하는 방법은 다른 교점 R의 X축 대칭이고, ( 기하학적 연산 )점 P와 상수 N의 곱은 점과 점의 합을 여러 번 반복한다. [4]
- 군 (Group)
- 군은 하나의 이항 연산자에 대해서 특수한 조건을 가진 수의 집합으로 모든 정수는 덧셈에 대해서 군을 이룬다. 정수를 정수와 더하면 정수가 나올 것이고 더샘은 결합법칙이 성립하는 연산으로 정수 안에는 더샘의 항등원인 0이 있고, 역원인 음수가 있다. 예를 들면 42의 역원은 -42이고 항등원은 0이라면, 모든 정수가 덧셈에 대해서 군을 이룬다. 정수와 같이 덧셈에 대한 군을 덧셈 군이라 부르고, 곱셈에 대해서 군이 성립하면 곱셈 군이다. [5] 요약하면 군은 정의된 연산자에 대해서 닫혀있어야 하고, 연산자에 대해서 결합법칙이 성립되어야 하며, 군 안에는 항등원과 역원이 있어야 한다. 군은 역원이 없으며, 2의 곱셈에 대한 역원은 1/2인데 이는 정수가 아닌 유리수 라고 하면 유리수에는 0이 있는데, 0은 곱셈에 대한 역원이 존재하지 않는다.(1/0은 계산할 수 없다)따라서 0을 제외한 유리수가 곱셈군을 이룬다. 또는 모든 타원곡선에는 다음과 같은 두 점을 더하는 매우 신기한 연산이 있다. 두 점 P = (x1 , y1)와 Q = (x2 , y2) 가 있다고 할 때, 이들의 합 P+Q는 이렇다.
- P와 Q를 잇는 직선 l은 타원곡선과 다른 한 점 R = (x3 , -y3)에서 만난다.
- R을 x축에 대칭시킨 S = (x3 , y3)가 P+Q가 된다.
- 예외규칙 으로 무한점 ∞에 대해서는 "∞을 지나는 직선은 y축과 평행한 직선이다" 라는 규칙을 적용시키는데 l이 y축에 평행해서 다른 일반 점하고 안 만날 때는, R은 ∞로 정의 하고, P=∞일 때는, l은 'Q를 지나고 y축에 평행한 직선'이 된다.
- 예외규칙 으로 l이 다른 한 점 R에서 만나지 않을 경우에는, l은 P 또는 Q에서 접할 것이고 이 때 R은 l이 접하는 점이 된다.
- 예외규칙 으로 P=Q인 경우에는 l은 'P에서 그은 접선'으로 정의 하는데 l이 다른 한 점 R에서 만나지 않는다면 l은 P에서 변곡점을 가져야 하며, 이 때 R은 P로 생각한다.
- 예외규칙 으로 ∞에서 그은 접선은 ∞에서 변곡점을 가진다. ∞를 x축에 대칭시키면 ∞이다.
- 타원곡선 군에서의 덧셈의 특성
- 무한대 점은 O로 표기하며 타원곡선 위의 임의의 점 P에 대해서 P+O=P가 성립되며, 무한대 점은 덧셈 상의 항등원이 된다.
- 타원곡선 위의 임의의 점 P에 대해서 P+Q=O를 만족하는 점 Q가 존재하는데 Q=-P로 나타내며 뺄셈 R-S는 R+(-S) 로 정의되고, 점 -P는 점 P의 X축의 대칭점이 되기 때문에 점 P의 좌표가 (x, y)이면 점 -P의 좌표는(x, -y) 이 된다.
- 타원곡선 위의 임의의 점 P, Q와 R에 대해서 P+(Q+R)=(P+Q)+R이 성립한다. 타원곡선 위의 임의의 점 P와 Q에 대해서 P+Q=Q+P가 성립하므로 타원곡선 군은'가환군'이 된다.
- 타원곡선 위에서의 기하학적 연산
- 타원곡선 위에서의 기하학적 연산은 그대로 대수적인 연산으로도 설명이 된다. (x1, y1), (x2, y2), (x3, y3)'를 각각 점 P, Q, S=P+Q의 좌표라 한다면, 점 P+Q의 좌표(x3, y3)를 통해서 표현하고자 x1, x2, y1, y2 을 통해서 표현하고자 한다. R = (x3, y3)=-S가 성립되므로 y=α x+β를 점 P와 Q를 지나는 선의 방정식이다. 만약, (α x+β) 2 = x3+ax+b가 성립하면 점 P와 Q를 지나는 선 위의 점(x, α x+β)은 타원 곡선 위의 점이 되고, 3차 방정식 x3 - (α x+β) 2 + ax+b의 각각의 근에 대하여 한 개의 교차점이 존재하게 된다. (x1, αx1+β)'과 (x2, αx2+β)는 타원곡선 위의 두 점 P와 Q이기 때문에 이미 x1, x2가 근임을 알고 있다. 차수가 가장 높은 항의 계수가 1인 다항식에서 그 다항식에 존재하는 모든 근의 합은 차수 가두 번째로 높은 항의 계수에‘-’를 붙은 값과 동일하기 때문에 x1+ x2 + x3 = α2, 이 된다. 나머지 근은 x3 = α2 - x1 - x2와 y3 = αx3+β = y1 + α(x3 - x1)이 된다. P+Q에서 P=Q가 되며 는 점 P에서의 미분 값이 되기 때문에 음함수 미분을 하면 2yy'=3x2 / 2 y1 가 된다.[6]
< 예제 >
- y2 = x3-17x+16 에 의해서 정의되는 타원곡선 위의 두 점 P=(0, -4), Q=(1, 0) 이 주어졌을 때, P+Q는 다음과 같이 구할 수 있다. 즉, x1=0, y1 =-4, x2 =1, y2 =0 을식-1에 대입하면 을 얻게 되므로 P+Q=(15, -56) 이 된다. 실수 계산은 일반적으로 느리며 또한 반올림에 따른 오차로 인하여 정확하지가 않기 때문에 암호 응용에는 적합하지 않아서, 암호 시스템 구축을 위해서는 유한체위에서 정의된 타원곡선 군이 이용된다. P가 소수일 때 유한체 GF(P) 상에서의 타원곡선은 a, b∈GF(P)의 경우에 방정식 y2 mod p =x3+ax+b mod p를 만족하는(x, y) 점들의 집합과 무한대 점 O를 의미하고 x, y∈GF(P)이며, 4a 3 + 27b ≠0 (mod p)이면 타원곡선 군이 정의된다.[6]
- 타원곡선 이산대수 문제
- 소수 p에 대해서 GF(p)를 p개의 원소로 구성된 유한체라 하면, 타원곡선 위의 점 P의 위수 t는 TP=O를 만족하는 가장 작은 정수 t로 정의되고, GF(P) 상에서 정의된 타원곡선과 점 Q, 그리 고위수가 t인 타원곡선 위의 점 P가 주어졌을 때 Q=XP를 만족하는 정수 x∈[0, t-1]을 구하는 것을 타원곡선 이산대수 문제이다. 타원곡선 이산대수 문제의 가장 직접적인 해결방법은 Q를 구할 때까지 단순히 P, 2P=P+P, 3P=P+P+P, …를 연속적으로 계산하는 것이지만 t의 값이 매우 클 경우에는 실효성이 게 되어 현재까지 알려진 가장 효율적인 알고리즘은 Pollard의 rho 알고리즘 으로서 번의타원곡선 덧셈이 소요된다. Pohlig-Hellman알고리즘 역시 적용이 가능하지만, t가 소수일 경우에는 실효성 이 없어지게 되면, 대부분의 학자에 의해서 타원곡선 이산대수 문제는 소인수 분해나 이산대수 문제보다 훨씬 더 어려운 문제로 인식이 된다. 타원곡선 이산대수 문제에 대한 좀 더 적극적인 공격은 Pollard의 rho 알고리즘에 기반을 두고 병렬처리를 가능하게 하는 특수목적의 하드웨어를 구축하는 것이다. 하지만 이런 공격도 t2160 인 경우에는 불가능하게 된다. 현재 타원곡선 암호에 적용 가능한 타원곡선 이산대수의 t 값은 단기적으로 150bit, 장기적으로 180bit 이상이 권고된다.[6]
체에대한 타원곡선[편집]
- 실수체 위의 타원곡선
- 실수 체 상에서, 타원곡선은 실수 a와 b에 대해 방정식 y2 = x3 + ax + b로 정의되는 평면 곡선으로 1이 아닌 3차 항의 계수와 0이 아닌 2차 항의 계수는 x, y를 다시 정의함으로써 흡수시킬 수 있기에 우변이 임의의 x의 3차식이면 언제나 이런 형태의 식을 바이어슈트라스 방정식으로 만들 수 있다. 타원곡선의 정의에는 이 곡선이 비특이 하다는 조건이 포함되고, 기하학적으로 말하자면 이는 곡선의 그래프가 첨 점이나 교차점이 없다는 뜻으로 판별식 Δ = −16(4a 3 + 27b 2)이 0이 아니라는 대수적인 조건과 동치이다. 비특이 대수 곡선은 판별식이 양수일 경우 두 개의 연결 성분을 가지고, 음수일 경우에는 하나의 연결 성분만을 가진다. 옆의 그래프에서 첫 번째 곡선의 판별식은 64, 두 번째 곡선의 판별식은 −368이다.
- 복소수체 위의 타원곡선
- 복소수체에서의 타원곡선은 1차원 아벨 다양체이다. 종수가 1이므로, 기하학적으로 이는 원환면의 모양을 하고 있다. 임의의 타원곡선가 주어졌다면, 원환면으로 여길 수 있으며, 복소 구조를 갖춘 원환면은 격자에 대한 몫공간 로 여길 수 있다. 그렇다면 이 원환면에서 타원곡선으로 바이어슈트라스 타원함수를 사용해 다음과 같은 사상을 정의할 수 있다.
- 바이어슈트라스 타원함수는 다음과 같은 항등식을 만족시킨다. 따라서 이는 인 타원 곡선과의 동형사상이다.
- 수체 위의 타원곡선
- 유리 수 체를 비롯한 다른 대수적 수 체에 대한 타원곡선은 수론에서 중요한 위치를 차지하는데 수 체에 대한 타원곡선의 점들은 보통 유리 점 이라 하고, 주어진 수 체 K에 대하여, 타원곡선 E의 K-유리 점들의 집합 E(K)는 아벨 군을 이룬다. 모델-베유 정리에 따라서, 타원곡선의 유리점군 E(K)는 항상 유한 생성 아벨 군이며, 따라서 그 계수와 꼬임 부분 군에 의해 주어진다. 유리수체 의 경우, 유리 점 군의 꼬임 부분 군은 메이저 꼬임 정리에 따라 15가지의 가능한 군 가운데 하나이며, 다른 수 체의 경우에도 메이저 꼬임 정리와 유사한, 가능한 꼬임 부분군 목록들이 존재한다.
- 유한체 위의 타원곡선
- 유한체 에 대한 타원곡선은 유한개의 점들로 이루어져 유한 군을 이루고 점의 개수를 세는 것은 일반적으로 매우 어려운 문제이며, 수론의 주요 연구 분야 가운데 하나이다. 하세 정리에 따라 위의 타원곡선 E에 대하여, 그 점의 수 는 다음과 같은 상계 및 하계를 가진다. 유한체에 대한 타원곡선의 점들이 이루는 유한군은 항상 두 순환군의 곱으로 유한체 에 대한 타원 곡선 은 72개의 점 을 갖고, 그 군 구조는 2차 순환군과 36차 순환군의 곱이다. 유한체에 대한 타원곡선은 타원곡선 암호를 정의 하는데 사용한다.
공개키 암호[편집]
- 다른 공개키 암호와 비교
- RSA 공개키 암호나 DSA 디지털 서명의 경우에 법 n과 p의 크기가 각각 1024bit 이상이 되고, 타원곡선 암호의 경우에는 160bit 이상이 요구되므로 타원곡선 암호의 경우에는 RSA나 DSA보다 짧은 키를 가지고도 높은 수준의 안전성이 보장되기 때문에 실제 구현에 있어서 안전성과 효율성이 모두 뛰어난 암호로 인식되고 있다.[6]
< 타원곡선 이산대수와 소인수 분해에 드는 계산량 > mips-year 163 160 191 186 239 234 359 354 431 426
512 768 1024 1280 1536
- 타원곡선 공개키 암호
- 이산대수에 기반을 둔 공개키 암호는 타원곡선 이산대수에 기반을 둔 공개키 암호로 전환된다. 두 시스템에서의 암호화 및 복호화 그리고 공개키 및 개인키를비교하면, 타원곡선 공개키 암호에서는 공개키 G와 Y 그리고 평문 M과 암호문 C1과 C2는 모두 타원곡선 위의 점으로 두 시스템 간의 기본적인 차이점은 ? 공개키 암호에서의 지수 승과 곱셈 작업이 타원곡선 공개키 암호에서는 각각 배수와 덧셈 작업으로 전환된다.[6]
< ElGamal 공개키 암호와 타원곡선 공개키 암호 비교 > ELGamal 공개키 암호 타원곡선 공개키 암호 공개키 개인키 암호화 복호화
각주[편집]
- ↑ 〈타원 곡선 [楕圓曲線]〉,《다음 한국어사전》
- ↑ 한국정보통신 기술협회 공식홈페이지 -https://www.tta.or.kr
- ↑ 〈타원곡선〉, 《위키백과》
- ↑ 우주를줄게, 〈타원곡선 암호과 이더리움 전자서명〉, 《티스토리》
- ↑ Luavis, 〈타원곡선 디피 헬만〉,《생계코딩 이야기》, 2019-02-17
- ↑ 6.0 6.1 6.2 6.3 6.4 코원동서, 〈타원곡선 암호 시스템(공개키 암호)〉
참고자료[편집]
- 우용이, 〈타원곡선〉, 《네이버》, 2017-11-27
- 코원동서, 〈타원곡선 암호 시스템(공개키 암호)〉
- 〈타원곡선〉, 《위키백과》
- 〈타원곡선〉, 《나무위키》
- Crocus, 〈타원 곡선 암호학(Elliptic Curve Cryptography)〉
- 〈타원곡선〉, 《수학노트》
- 우주를줄게, 〈타원곡선 암호과 이더리움 전자서명〉, 《티스토리》

 위키원
위키원