논리곱

논리곱

논리곱(conjunction, AND)이란 수리 논리학에서, 주어진 복수 명제 모두가 참인지를 나타내는 논리 연산이다. 논리곱은 임의의 명제를 나타낼 때, '그리고(and)'이라는 논리적 언어로 연결된 합성명제이다.

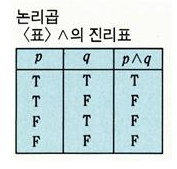
두 임의의 명제 p와 q를 논리어「그리고(and)」를 사용하여「p 그리고 q」(p and q)라고 표현한 합성명제(合成命題). 합접(合接) 또는 연합명제라고도 한다. 기호 p∧q로 표시하고「p 그리고 q」라고 읽는다. p∧q는 두 명제 p와 q를 동시에 주장하며 그 진리값은 <표>와 같다. 진리값은 p,q의 양쪽이 참일 때만 참이며 p,q의 한쪽 또는 양쪽이 거짓일 때는 거짓이다(표에서 T는 참, F는 거짓).

예시

• 「내 키는 160 cm 이상이다」
• 「내 몸무게는 50 kg 이상이다」

위 두 명제의 논리곱은

• 「내 키는 160 cm 이상이고, 내 몸무게는 50 kg 이상이다.」

특징

논리곱은 부정과 논리합으로 나타낼 수 있다.

P ∧ Q = ¬(¬P ∨ ¬Q) 반대로, 부정과 논리곱을 이용해서 논리합을 표현할 수 있다.

P ∨ Q = ¬(¬P ∧ ¬Q)

동작원리

논리곱(AND)은 · 로 표현하고 "그리고"를 의미한다. 입력 값이 둘 다 참(1)일 경우에만 결과가 참(1)이 되는 논리를 가진다. 입력값의 두 가지 조건이 모두 만족해도 된다.

공원 입장료가 "8세 초과이고 65세 미만이면 3,000원"이라는 조건을 논리식으로 표현해 보면

나이·값> 8>그리고 나이·값>65

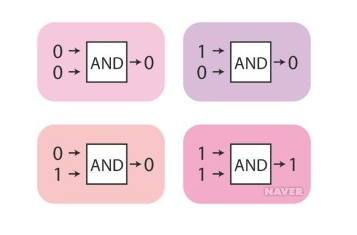
입력이 두 개라고 했을 때 논리곱 연산 결과는 어떻게 될까? 입력값이 두 개이므로 00, 01, 10, 11일 때 각각의 경우를 살펴보면 다음과 같다.

입력값이 두개일 경우

 

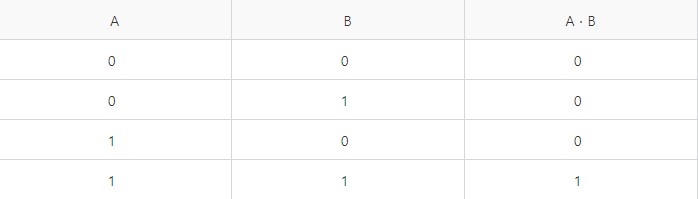
논리곱 연산 결과를 표로 정리해 보면,

설명

 

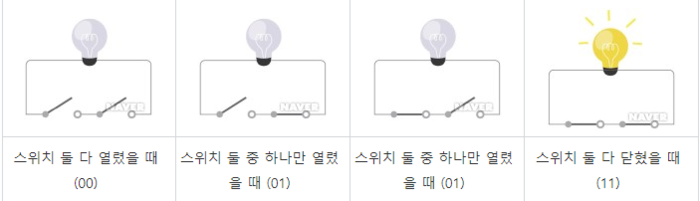
그림은 스위치 2개, 전구가 1개 있는 직렬회로이다.

스위치 예를 든 논리곱과 같은 논리

 

스위치가 열렸을 때를 0 닫혔을 때를 1이라고 할 때, 직렬회로는 스위치가 둘 다 닫혔을 때만 전구에 불이 들어온다. 즉 입력값에 모두 1일 때 참이 되는 논리곱(AND)과 같은 논리로 동작한다.

논리곱(AND)의 논리를 집합으로 표현한 그래프

 

참고자료

• 〈논리곱〉, 《위키백과》
• 〈논리곱〉, 《네이버지식백과》
• 〈논리곱〉, 《사이언스올》
• 〈논리연산〉, 《네이버지식백과》

같이 보기

• 논리연산
• 논리합
• 부정논리합
• 부정연산

이 논리곱 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반