논리합

논리합(disjunction, 論理合, OR)은 수리 논리학에서 주어진 복수 명제에 적어도 1개 이상의 참이 있는지를 나타내는 논리 연산이다. 논리합은 두개의 임의의 명제 P,Q를 논리어「또는 (or)」을 사용하여「P 또는 Q」(P or Q)라고 표시하는 합성명제(合成命題)이다. 이접(離接)·선언명제(選言命題)라고도 한다. 기호 P Q라고 표시하며, 이것은 두 명제 가운데 어느 쪽인가 한 쪽을 주장하는 것이다.

예시

• 내 키는 160cm 이상이다.

내 몸무게는 50kg 이상이다. 위 두 명제의 논리합은

내 키는 160cm 이상이거나 나의 몸무게는 50kg 이상이다. 가 된다.

진리표

P Q의 진리값은 표와 같이 정의한다.

명제 P	명제 Q	P ∨ Q
참	참	참
참	거짓	참
거짓	참	참
거짓	거짓	거짓

즉, P,Q 양쪽이 다 거짓일 때만 거짓이고 P,Q의 한쪽 또는 양쪽이 참일 때는 참이다.

동작논리

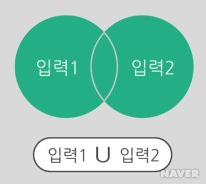
논리합(OR)은 +로 표현하고 "또는"을 의미한다.

입력값에 참(1)이 한 개 이상이면 결과값이 참(1)이 되는 논리를 가진다. 입력값의 두 가지 조건 중 하나만 만족해도 된다.

공원 입장료가 "나이가 8세 미만 무료, 65세 이상 무료"라고 했을 때 논리식으로 표현해 보면

나이 · 값 > 8 > 또는 나이 · 값 > 65

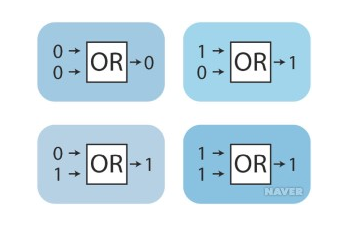
입력이 두 개라고 했을때 논리합 연산 결과는 어떻게 될까?

입력값이 두 개이므로 00, 01, 10, 11일 때 각각의 경우를 살펴보면 다음과 같다.

입력값이 두개일때 경우

 

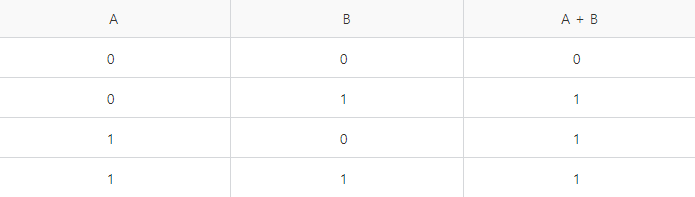
논리합 연산 결과를 표로 정리해 보면,

논리합 연산 결과

 

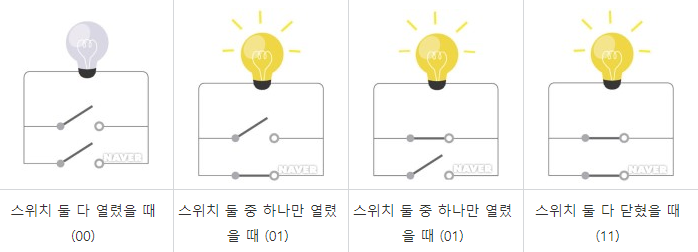
그림은 스위치 2개, 전구가 1개 있는 병렬회로이다.

스위치 2개, 전구 1개 병렬회로 동작논리

 

스위치가 열렸을 때를 0 닫혔을 때를 1이라고 할 때, 병렬회로는 최소한 스위치가 둘 중에 하나만 닫혀도 전구에 불이 들어온다. 즉 입력값에 최소한 1이 한 개만 있어도 참이 되는 논리합(OR)과 같은 논리로 동작한다.

논리합(OR)의 논리를 집합으로 표현한 그래프

 

참고자료

• 〈논리 연산〉, 《나무위키》
• 〈논리연산〉, 《네이버지식백과》
• 〈논리연산〉, 《네이버지식백과》
• 〈논리연산〉, 《위키백과》

같이 보기

• 논리곱
• 논리연산
• 논리부정
• C언어

이 논리합 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반