"부정논리곱"의 두 판 사이의 차이
잔글 (→같이 보기) |
잔글 |
||
| 1번째 줄: | 1번째 줄: | ||
| − | '''부정논리곱'''(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. '''NAND'''라고도 한다. | + | '''부정논리곱'''(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. '''NAND'''(낸드)라고도 한다. |
| + | |||
== 개요 == | == 개요 == | ||
Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다. | Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다. | ||
| 75번째 줄: | 76번째 줄: | ||
{{암호 알고리즘|검토 필요}} | {{암호 알고리즘|검토 필요}} | ||
| − | |||
2020년 1월 6일 (월) 23:39 판
부정논리곱(否定論理積, NAND)은 주어진 복수의 명제 중 거짓이 포함되었는지 보는 논리 연산이다. NAND(낸드)라고도 한다.
개요
Not AND. 논리곱의 결과값을 부정한 것이다. 즉, 두 명제가 모두 참이면 거짓값을 돌려주고 그 외에는 참값을 돌려준다. 참고로 NAND만을 통해 다른 논리 연산식을 모조리 구현할 수 있기 때문에 현재 사용되는 플래시 메모리들은 대부분이 NAND 회로로 구성되어 있다.
NAND 연산 결과 입력값 반환값 0, 0 1 0, 1 1 1, 0 1 1, 1 0
특징
일반적으로 NAND는 다음과 같이 정의된다.
A NAND B = NOT (A AND B)
진리표
명제 P 명제 Q P NAND Q 참 참 거짓 참 거짓 참 거짓 참 참 거짓 거짓 참
응용
일반적으로 논리 연산은 논리곱(AND), 논리합(OR), 논리부정(NOT)의 구성으로 표현 가능하다. 하지만, NAND는 모든 논리 연산을 표현할 수 있다. AND, OR, NOT 역시 NAND로 표현할 수 있다.
- NOT A = A NAND A
- A AND B = NOT ( A NAND B ) = ( A NAND B ) NAND ( A NAND B )
- A OR B = ( NOT A ) NAND ( NOT B ) = ( A NAND A ) NAND ( B NAND B )
초기의 집적 회로(표준 논리 IC)는 부품이 고가였기 때문에 가장 회로 구성이 간단한 NAND를 이용하여 다양한 논리 회로를 설계하였다.
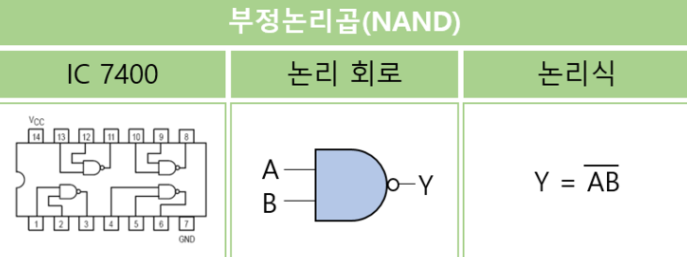
부정논리곱(NAND)의 논리 기호의 표현과 이용되는 IC칩
대표적인 NAND 게이트 IC의 TTL는 74LS00(2입력), 74LS10(3입력), 74LS20(4입력)이 있고, CMOS는 CD4011(2입력), CD4023(3입력), CD4012(4입력)가 있다.
참고자료
- 〈논리 연산〉, 《나무위키》
- 〈부정논리곱)〉, 《위키백과》
- 〈불 대수의 기본 연산과 논리게이트(2)〉, 《네이버 블로그》
같이 보기

 위키원
위키원