CRC-32

CRC-32은 Cyclic Redundancy Check (CRC) 방식중의 하나이며 CRC 알고리즘 계산을 추진할 때 CRC32 다항식 (Polynomial) 을 사용한다. CRC는 네트워크 데이터블록 또는 파일 등 데이터에 근거하여 짧고 간단하며 자리수가 고정 된 검증코드를 발생시키는 채널코딩기술 (Channel Coding Techniques) 이며 주로 데이터 전송 또는 저장 후에 발생할 수 있는 오류 등을 감지 또는 검증하는데 사용된다. CRC는 1961년에 미국의 정보와 컴퓨터과학 전문가 W. Wesley Peterson 이 발명하였다.

개요

CRC-32은 Cyclic Redundancy Check (CRC) 방식중에 CRC32 다항식을 적용하여 검증코드 (체크섬;Checksum) 를 취득하고 이를 통신에 적용하는 채널코딩기술이다.

적용시 송신자측은 전송하고자 하는 메세지에 산출 된 체크섬을 더하여 전송하고 수신자측은 체크섬 산출 시 사용하였던 다항식을 그대로 적용하여 수신한 메세지에 나누기를 적용하여 산출 된 값이 Zero인지를 판단한다. Zero 이면 데이터 송수신이 정확히 진행되었고 아닐 경우 송수신 오류가 발생하였다고 판단한다.

CRC검증작업에서 실수(검증작업에서 오류를 발견못하는) 할 확률은 1/2^32이다. 실제 작업중에는 실수가 없다고 과언해도 무리는 아니다.

ISO, ANSI 등 에서 적용하는 CRC-32 다항식은 x³² + x²⁶ + x²³ + x²² + x + x¹⁶ + x¹² + x¹¹ + x¹⁰ + x⁸ + x⁷ + x⁵ +x⁴ + x² + x + 1 이다.

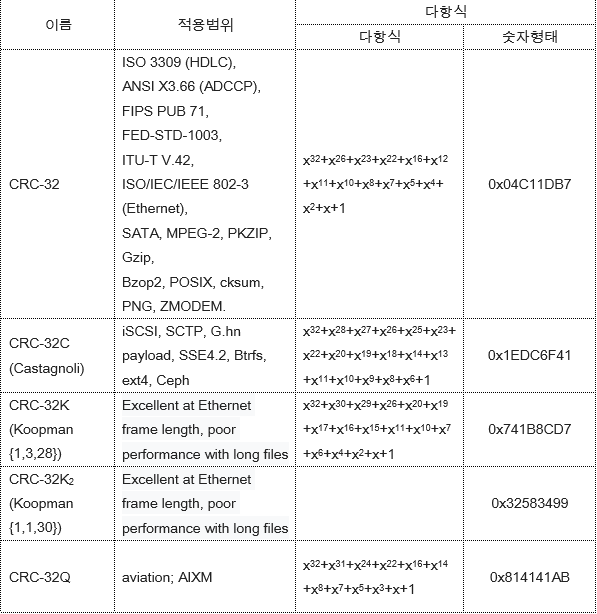
CRC-32 산하에는 적용하는 다항식에 따라 CRC-32 알고리즘군이 구성되어 있으며 넓은 영역에서 사용된다. 구체적으로 아래시트를 참조할 수 있다.

CRC-32 알고리즘 군

CRC원리

▷ 다항식과 바이너리 코드

다항식과 바이너리코드사이에는 직접적인 대응관계가 존재한다. X의 최고지수가 바이너리의 최고위와 대응되며 아래 각 항들이 일일이 각 제곱과 대응된다. 지수가 있을 경우는 1로 표시하고 없는 경우에는 0으로 표기한다. X의 최고지수가 R일 경우 R+1 비트 바이너리 코드로 전환할 수 있다. 예를 들면 다항식 G(x)=x4 + x3 + x + 1 은 바이너리 코드 11011로 전환할 수 있다.

▷ 다항식

송수신 양측이 약정하여 메세지 데이터 처리에 사용하는 바이너리 데이터이며 데이터 전송 전반과정에서 불변한다. 다항식은 용도에 따라 상당수 분야에서 과학가들이 이미 정해놓았다.

▷ CRC원리

전송하고자 하는 어떤 데이터에 CRC 알고리즘을 적용하여 k 비트 바이너리 서열이 형성되고 형성된 서열은 다항식 (Pplynomial) 이라 불리우는 바이너리 서열에 나뉜다. 나뉜 뒤, r 비트의 나머지를 체크섬 (Checksum) 이라하며 송신측은 (k + r) 비트의 신규 바이너리 서열을 만들어 전송한다.

수신측은 접수 한 바이너리 서열 (서열에는 체크섬이 포함되어 있다) 을 송신측에서 사용하였던 다항식으로 나누기를 추진한다. 나눈 결과가 zero 이면 송신은 정확히 진행되었고 아닐 경우 송신오류가 발생하였다고 판단한다.

여기서 나누기 계산은 산술계산의 나누기가 아니고 Logic 계산 XOR를 가르킨다.

CRC 검증코드 수동계산 사례

▶ 작업목표: 다항식 G(x)=x4 + x3 + 1 일때 바이너리 코드 10110011의 CRC 검증코드를 산출한다.

▶ 계산내역:

1)다항식의 바이너리 서열

G(x)=x4 + x3 + 1, 대응되는 바이너리 서열 11001 (설명: x4 는 5비트 바이너리 서열의 최고위치를 가르키고 Logic 값은 1을 나타내며 x3 은 5비트 서열의 그 다음 위치, Logic 값은 1을 나타낸다. x2 는 없기에 3번째 위치를 가르키고 Logic 값은 0을 나타낸다. 이런 식으로 마지막까지 처리하면 위의 바이너리 서열을 얻을 수 있다.)

2)검증코드는 4자리수를 맞추어야 함으로 바이너리 코드 10110011에 0 4개를 첨부하여 신규 서열 1011 0011 0000 을 얻는다.

3)검증코드 산출계산

• 메시지 = 10110011
• 다항식 = 11001

CRC 수동계산 사례

4)신규 취득 바이너리 서열

메시지 1011001를 대상으로 CRC 알고리즘 계산 추진 후 신규 서열 1011 0011 0100 이 형성되었으며 이가 나중에 공식적으로 전송하는 발송메세지가 된다.

참고자료

• "Cyclic redundancy check", Wikipedia

같이 보기

• CRC-16

이 CRC-32 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반