"에스박스"의 두 판 사이의 차이
잔글 (→Rijendael S-box) |
잔글 |
||
| 12번째 줄: | 12번째 줄: | ||
DES의 8개의 S-box는 설계자만이 알고 있는 취약성이 암호에 심어졌을지도 모른다는 우려 때문에 수년 동안 집중적인 연구의 대상이었다. S-box 설계기준은 결국 차등암호분석의 일반적 재발견 후에 발표되었고(Copersmith 1994) 이러한 특정 공격에 대한 저항을 증가시키기 위해 세심하게 조정되었음을 보여준다. Biham과 Shamir는 S-box를 조금만 수정해도 DES를 크게 약화시킬 수 있다는 것을 발견했다. | DES의 8개의 S-box는 설계자만이 알고 있는 취약성이 암호에 심어졌을지도 모른다는 우려 때문에 수년 동안 집중적인 연구의 대상이었다. S-box 설계기준은 결국 차등암호분석의 일반적 재발견 후에 발표되었고(Copersmith 1994) 이러한 특정 공격에 대한 저항을 증가시키기 위해 세심하게 조정되었음을 보여준다. Biham과 Shamir는 S-box를 조금만 수정해도 DES를 크게 약화시킬 수 있다는 것을 발견했다. | ||
| − | == | + | == 레인달 에스박스 == |
| − | + | 레인달 에스박스(Rijndael S-box)는 [[AES]](Advanced Encryption Standard) 암호 알고리즘을 기반으로 한 [[레인달]](Rijendael, [rɛindaːl]) 암호에 사용된 대체 박스이다. | |
| − | === | + | === 포워드 에스박스 === |
[[파일:AES S-box.png|썸네일|500픽셀|오른쪽|]] | [[파일:AES S-box.png|썸네일|500픽셀|오른쪽|]] | ||
| − | S-box는 8비트 입력 c를 8비트 출력 '''s=S(c)'''에 매핑한다. 입력과 출력 모두 '''GF(2)'''를 통한 다항식으로 해석된다. 첫째, 입력은 '''GF(2<sup>8</sup>)=GF(2)[''x'']/(''x''<sup>8</sup> + ''x''<sup>4</sup> + ''x''<sup>3</sup> + ''x'' + 1)'''의 곱셈 역에 매핑된다. 역이 없는 제로(zero)는 0으로 매핑된다. 이러한 변형은 발명가 카이사 니베르크(Kaisa Nyberg)의 이름을 따서 "니베르크 S-box | + | S-box는 8비트 입력 c를 8비트 출력 '''s=S(c)'''에 매핑한다. 입력과 출력 모두 '''GF(2)'''를 통한 다항식으로 해석된다. 첫째, 입력은 '''GF(2<sup>8</sup>)=GF(2)[''x'']/(''x''<sup>8</sup> + ''x''<sup>4</sup> + ''x''<sup>3</sup> + ''x'' + 1)'''의 곱셈 역에 매핑된다. 역이 없는 제로(zero)는 0으로 매핑된다. 이러한 변형은 발명가 카이사 니베르크(Kaisa Nyberg)의 이름을 따서 "니베르크 에스박스"(Nyberg S-box)로 알려져 있다. 곱하기 역은 다음과 같은 아핀 변환을 사용하여 변환한다. |
[[파일:에스박스-1.png|썸네일|400픽셀|가운데|]] | [[파일:에스박스-1.png|썸네일|400픽셀|가운데|]] | ||
여기서 '''[''s''<sub>7</sub>, ..., ''s''<sub>0</sub>]'''은 S-box 출력이고 '''[''b''<sub>7</sub>, ..., ''b''<sub>0</sub>]'''은 벡터로서 곱셈의 역수이다. | 여기서 '''[''s''<sub>7</sub>, ..., ''s''<sub>0</sub>]'''은 S-box 출력이고 '''[''b''<sub>7</sub>, ..., ''b''<sub>0</sub>]'''은 벡터로서 곱셈의 역수이다. | ||
| − | 이 아핀 변환은 바이트의 다중 회전을 벡터로 합한 것이다. 여기에서 더하기는 XOR 연산이다. | + | 이 아핀 변환은 바이트의 다중 회전을 벡터로 합한 것이다. 여기에서 더하기는 [[XOR]] 연산이다. |
<math> s = b \oplus (b \lll 1) \oplus (b \lll 2) \oplus (b \lll 3) \oplus (b \lll 4) \oplus 63_{16}</math> | <math> s = b \oplus (b \lll 1) \oplus (b \lll 2) \oplus (b \lll 3) \oplus (b \lll 4) \oplus 63_{16}</math> | ||
| 35번째 줄: | 35번째 줄: | ||
다른 하나는 다음과 같다: <math>s = (b \times 31_d) \operatorname{mod} 257_d \oplus 99_d</math> | 다른 하나는 다음과 같다: <math>s = (b \times 31_d) \operatorname{mod} 257_d \oplus 99_d</math> | ||
| − | === | + | === 인버스 에스박스 === |
[[파일:역방향 에스박스.png|썸네일|400픽셀|오른쪽|역방향 에스박스|]] | [[파일:역방향 에스박스.png|썸네일|400픽셀|오른쪽|역방향 에스박스|]] | ||
| − | Inverse S- | + | 인버스 에스박스(Inverse S-box)는 단순히 에스박스의 역방향 실행이다. 예를 들어, 0xb8의 역방향 S-box는 0x9a이다. 먼저 입력 값의 역방향 아핀 변환을 계산하고, 그 뒤에 곱셈 역변형을 계산한다. 역방향 아핀 변환은 다음과 같다. |
[[파일:역방향아핀변환.png|썸네일|400픽셀|가운데|역방향 아핀변환|]] | [[파일:역방향아핀변환.png|썸네일|400픽셀|가운데|역방향 아핀변환|]] | ||
역방향 아핀 변환은 벡터로서의 바이트의 다중 회전 합계를 나타내기도 하며, 여기서 추가는 XOR 연산이다. | 역방향 아핀 변환은 벡터로서의 바이트의 다중 회전 합계를 나타내기도 하며, 여기서 추가는 XOR 연산이다. | ||
| 53번째 줄: | 53번째 줄: | ||
<youtube>0UhNURV8CE8</youtube> | <youtube>0UhNURV8CE8</youtube> | ||
<youtube>skMih0DLR3g</youtube> | <youtube>skMih0DLR3g</youtube> | ||
| + | |||
== 참고자료 == | == 참고자료 == | ||
* "[https://en.wikipedia.org/wiki/S-box S-box]", ''Wikipedia'' | * "[https://en.wikipedia.org/wiki/S-box S-box]", ''Wikipedia'' | ||
| 60번째 줄: | 61번째 줄: | ||
* [[AES]] | * [[AES]] | ||
* [[DEX]] | * [[DEX]] | ||
| + | * [[레인달]] | ||
{{암호 알고리즘|검토 필요}} | {{암호 알고리즘|검토 필요}} | ||
2020년 1월 12일 (일) 15:47 판
에스박스(S-box, substitution box)는 암호학 분야의 하나의 기본 패킷으로서 그 기능은 데이터의 비선형 치환을 실현하는 것이다. 암호학에서 에스박스는 대체를 수행하는 대칭 키 알고리즘의 기본 구성요소이다. 블록 암호에서는 일반적으로 키와 암호텍스트(섀넌의 혼란 속성)사이의 관계를 모호하게 하는데 사용된다.
일반적으로 S-box는 몇 개의 입력 비트 m을 취하여 일부 출력 비트수 n으로 변환한다. 여기서 n은 반드시 m과 동일하지 않다. m×n S-box는 각각 2m 단어의 n비트로 구성된 룩업 테이블로 구현될 수 있다. 고정 테이블은 데이터 암호화 표준(DES, Data Encryption Standard)에서와 같이 일반적으로 사용되지만, 일부 암호에서는 테이블이 키(예: Blowfish 및 Twofish 암호화 알고리즘)에서 동적으로 생성된다.
응용
에스박스는 DES(Data Encryption Standard), AES(Advanced Encryption Standard), SM1(국가암호 알고리즘), SM4(국가암호 알고리즘)와 같은 대칭 암호화 알고리즘에 주로 사용된다.
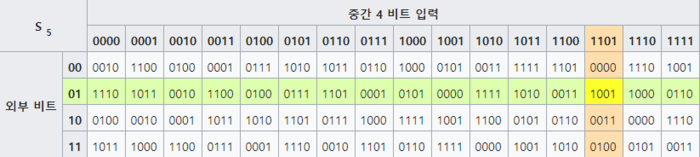
고정 테이블의 좋은 예로는 DES(S5)에서 S-box를 들 수 있으며, 6비트 입력을 4비트 출력에 매핑한다.
6비트 입력이 주어지면, 4비트 출력은 바깥쪽 2비트(첫 번째 비트 및 마지막 비트)를 사용하여 행을 선택하고, 안쪽 4비트를 사용하여 열을 선택하여 찾을 수 있다. 예를 들어, 입력 "011011"은 외부 비트 "01"과 내부 비트 "1101"을 가지고 있으며, 해당 출력은 "1001"이 될 것이다.
DES의 8개의 S-box는 설계자만이 알고 있는 취약성이 암호에 심어졌을지도 모른다는 우려 때문에 수년 동안 집중적인 연구의 대상이었다. S-box 설계기준은 결국 차등암호분석의 일반적 재발견 후에 발표되었고(Copersmith 1994) 이러한 특정 공격에 대한 저항을 증가시키기 위해 세심하게 조정되었음을 보여준다. Biham과 Shamir는 S-box를 조금만 수정해도 DES를 크게 약화시킬 수 있다는 것을 발견했다.
레인달 에스박스
레인달 에스박스(Rijndael S-box)는 AES(Advanced Encryption Standard) 암호 알고리즘을 기반으로 한 레인달(Rijendael, [rɛindaːl]) 암호에 사용된 대체 박스이다.
포워드 에스박스
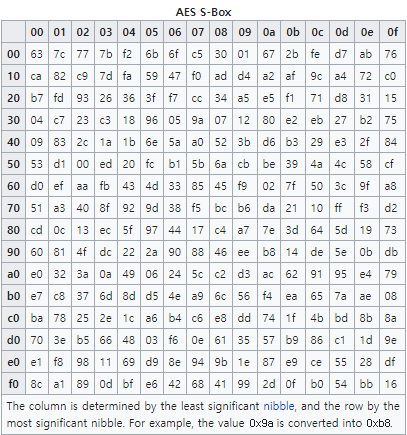
S-box는 8비트 입력 c를 8비트 출력 s=S(c)에 매핑한다. 입력과 출력 모두 GF(2)를 통한 다항식으로 해석된다. 첫째, 입력은 GF(28)=GF(2)[x]/(x8 + x4 + x3 + x + 1)의 곱셈 역에 매핑된다. 역이 없는 제로(zero)는 0으로 매핑된다. 이러한 변형은 발명가 카이사 니베르크(Kaisa Nyberg)의 이름을 따서 "니베르크 에스박스"(Nyberg S-box)로 알려져 있다. 곱하기 역은 다음과 같은 아핀 변환을 사용하여 변환한다.
여기서 [s7, ..., s0]은 S-box 출력이고 [b7, ..., b0]은 벡터로서 곱셈의 역수이다.
이 아핀 변환은 바이트의 다중 회전을 벡터로 합한 것이다. 여기에서 더하기는 XOR 연산이다.
여기서 b는 곱셈의 역수를 나타낸다. 는 IS bitwise XOR 연산자, 는 왼쪽 비트 단위의 순환 시프트이며 상수 6316 = 011000112 는 16진수로 주어진다 .
아핀 변환에 대한 등가 방정식은 다음과 같다.
여기서 s, b 및 c는 8비트 배열이고 c는 01100011이다.
다른 하나는 다음과 같다:
인버스 에스박스
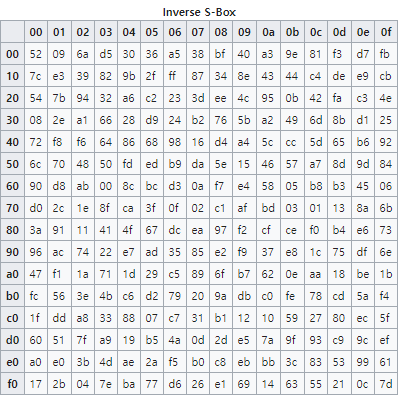
인버스 에스박스(Inverse S-box)는 단순히 에스박스의 역방향 실행이다. 예를 들어, 0xb8의 역방향 S-box는 0x9a이다. 먼저 입력 값의 역방향 아핀 변환을 계산하고, 그 뒤에 곱셈 역변형을 계산한다. 역방향 아핀 변환은 다음과 같다.
역방향 아핀 변환은 벡터로서의 바이트의 다중 회전 합계를 나타내기도 하며, 여기서 추가는 XOR 연산이다.
여기서 는 bitwise XOR 연산자, 은 왼쪽 bitwise 순환 이동이며, 상수 516 = 000001012</sub는 16진수로 주어진다.
설계기준
Rijdael S-Box는 특별히 선형 및 차등 암호해석에 내성을 갖도록 설계되었다. 이는 입력/출력 비트의 선형 변환 사이의 상관관계를 최소화하고 동시에 차이 전파 확률을 최소화함으로써 수행되었다.
Rijdael S-Box는 정적 S-box를 이용하는 암호에 내장된 백도어의 의심을 물리치는 Rijdael 암호로 대체될 수 있다. 저자들은 "평균" 상관관계/차이 전파 특성을 가진 S-Box를 사용할 경우 Rijdael 암호 구조가 차등 및 선형 암호해석에 대해 충분한 저항을 제공해야 한다고 주장한다.
동영상
참고자료
- "S-box", Wikipedia
- "Rijndael_S-box", Wikipedia
같이 보기

 위키원
위키원