타원곡선(elliptic curve)은 y^2 = x^3 + Ax + B 형태의 방정식으로 나타나는 곡선으로서, 첨점이나 교차점 등의 특이점이 없는 것으로 중근을 갖지 않는 임의의 3차 혹은 4차 다항식 P에 대해 y2 = P(x)는 곡면 종수 1의 비특이 평면 곡선의 방정식이며, 보다 일반적으로는 종수가 1인 임의의 비특이 대수 곡선을 타원 곡선이라 한다.
개요
타원곡선은 타원하고 별로 상관이 없고, 형태상으로는 타원보다는 중괄호에 가까운 모양 으로서 '타원곡선'이란 이름이 붙은 이유는 타원의 둘레를 구하기 위한 적분에서 유래했던 역사적 이유 지만, 현재는 그것과 전혀 상관없이 사용 되고 있으며, 항목이 등재된 이유는 이름이 혼동스러워서인 것은 아니고, 수학 전반에서 엄청난 중요성을 갖고 있기 때문이다. 같은 대상을 실해석학에서, 복소해석학에서, 대수기하학에서, 정수론에서 모두 이야기할 수 있는 경우는 그렇게 많지 않다.
특징
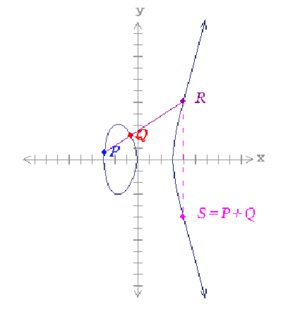
그림 1. 타원곡선y2=x3-9x-1와 타원곡선 위의 덧셈
- 그림 1은 y2=x3-9x-1 인 타원곡선이다. 실수 위에서의 타원곡선 군은 해당 타원곡선 위의 모든점들과 무한대 점이라고 명명된 특수 점으로 구성되고 여기에 덧셈이 정의된다. 점 P(x1 , y1)과 점 Q(x2, y2)를 더하기 위해서 P와 Q를 잇는 선을 그으면 타원곡선 위의 다른점 R과 교차한다. 만약 P=Q이면 점 P에 대한 접선을 그으면 된다. 계산한 점 R을 X축에 대칭을시킨 다른 점 S가 P+Q로 정의된다.
- 무한대 점은 O로 표기하며 타원곡선 위의 임의의 점 P에 대해서 P+O=P가 성립 되며, 무한대 점은 덧셈상의 항등원이 된다.
- 타원곡선 위의 임의의 점 P에 대해서 P+Q=O를 만족하는 점 Q가 존재하는데 Q=-P로 나타내며 뺄셈 R-S는 R+(-S)로 정의 되고, 점 -P는 점 P의 X축의 대칭점이 되기 때문에 점 P의좌표가 (x, y)이면 점 -P의 좌표는(x, -y)이 된다.
- 타원곡선 위의 임의의 점 P, Q와 R에 대해서 P+(Q+R)=(P+Q)+R이 성립한다. 타원곡선 위의 임의의 점 P와 Q에 대해서 P+Q=Q+P가 성립 하므로 타원곡선 군은'가환군'이 된다.
- 타원곡선 위에서의 기하학적 연산은 그대로 대수적인 연산으로도 설명 이 된다. (x1, y1), (x2, y2), (x3, y3)을 각각 점 P, Q, S=P+Q의 좌표라 한다면, 점 P+Q의 좌표(x3, y3)을 통해서 표현 하고자 x1, x2, y1, y2 을 통해서 표현하고자 한다. R = (x3, y3)=-S 가 성립 되므로 y=αx+β 를 점 P와 Q를 지나는 선의 방정식이라 한다면, [파일:K1.PNG|썸네일|400픽셀]
각주
참고자료
같이 보기
|
 이 타원곡선 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.
|
| 블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스
|
|
|
| 암호기술
|
개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산
|
|
|
| 논리연산
|
논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT)
|
|
|
| SHA
|
SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512
|
|
|
| MD
|
MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320
|
|
|
| 기타 해시
|
CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사
|
|
|
| 대칭키
|
AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES
|
|
|
| 비대칭키
|
PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호
|
|
|
| 영지식증명
|
영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명
|
|
|
| 양자암호
|
BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜
|
|
|
| 암호해독
|
기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독
|
|
|
| 암호학 인물
|
라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|
위키원
