형태보존암호
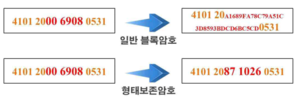
형태보존암호(Format-Preserving Encryption)란 평문과 암호문의 형태를 동일하게 유지한 채 암호화를 수행하는 암호화 알고리즘 및 기술이다. 기존의 운영 모드와는 달리 암호화를 거치더라도 메시지의 형태와 길이가 동일하도록 생성하는 암호기술이다. 암호화 장치를 작업 공간의 내부에 탑재하여 시스템과 유기적으로 연동한다.
개요
형태보존암호는 평문과 암호문의 형태를 동일하게 한다. 평문이 가진 형태를 온전히 유지한 채로 암호화를 수행하는 암호화 알고리즘이자 기술이다. 예를 들면 주민등록번호는 앞의 6자리와 뒤의 7자리 총 13자리 정수로 구성되어 있다. 여기서 보통은 13자리의 평문을 암호화하면 기법에 따라서 정해진 길이의 암호문이 출력된다. 만약 AES가 적용되었다면 128비트로 출력될 것이다. 그러나 형태보존암호에서는 13자리 정수라는 형태가 보존된 상태로 암호문이 출력된다. 따라서 어떤 응용프로그램은 암호문을 통해서 평문의 값을 알아낼 수는 없지만 어떤 종류의 값을 나타내는지는 알 수 있다. 형태보존암호의 형태는 일반적으로 정의역의 크기를 의미하며, 보통 크기가 작은 평문을 암호화할 때 사용된다. 형태보존암호의 주된 장점은 작은 크기의 평문을 암호화할 수 있다는 것이며, 평문과 암호문이 같은 형태이기 때문에 평문과 암호문 각각의 크기 또한 동일하고, 따라서 일반적인 블록 암호에서 상대적으로 긴 길이의 암호문을 전부 저장할 필요는 없다는 장점이 있다. 또, 기존의 시스템에 형태보존암호를 적용하고 싶을 때 기업이나 개인이 가지고 있는 기존의 시스템을 수정하거나 교체할 필요가 없어서 시간이나 비용 면에서 부담을 덜 수 있다. 형태보존암호는 대표적으로 prefix cipher, cycle-walking cipher, VFPE, FF1, FF3-1, FEA 등이 있다.[1] 블랙과 로가웨이가 도메인의 크기별/알고리즘의 복잡도별로 제안한 세 가지 방법인 prefix cipher, cycle-walking cipher, generalized-Feistel cipher은 여러 형태보존암호의 근간이 되었다.[2] 형태보존암호 방식의 대표적인 예로는 블록 암호 운영 모드를 이용한 방식을 들 수 있는데, 암호화 메시지 저장을 위해 별도로 추가적인 저장 공간을 확보할 필요가 없으며, 기업은 시스템 변경 최소화로 인한 암호화 시스템 구축 비용의 절감 효과를 얻을 수 있다. 이 운영 모드는 2016년에 미국 국립표준기술 연구소에서 관련 표준을 제정하였으며, 국내의 대표적인 형태보존암호로는 FEA가 있다.[3]
특징
일반적인 암호 알고리즘은 비트열을 비트열로 변환한다. 그러나 형태보존암호는 주민등록번호나 신용카드번호, 사회보장번호 등과 같이 비트열이 아닌 어떠한 특정 형태의 데이터를 갖진 경우에는 원본 데이터 값을 통일한 형태로 변환하기 때문에 기존 암호화 방식의 대체 기술이다.
- 트윅
형태보존암호에서 기밀성을 제공하기 위해서 정형화된 데이터에 추가로 입력하는 정보이다. 트윅은 꼭 비밀로 취급해서 보호받아야 하는 요소는 아니다. 암호화와 복호화의 함수 모두를 결정하기 때문에 키에서 변화할 수 있는 부분으로 간주한다.
- 파이스텔 구조
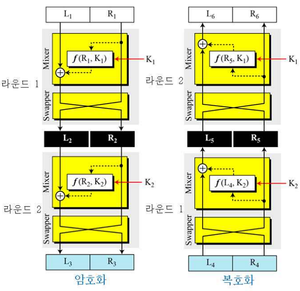
형태보존암호는 블록 암호의 파이스텔 구조에 기반한다. 파이스텔 구조는 암호화 방식이 특정한 계산 함수의 반복으로 이루어지는 구조를 말하며, 페스탈 구조라고도 불린다. 데이터를 두 부분으로 나누어서 좌우 두 부분에 교대로 비선형 변환을 적용하며, 치환과 순열을 번갈아서 수행한다. 암호화 및 복호화 과정에서 역함수가 필요 없다는 장점이 있으며, 구현 시에 스왑 단계 때문에 연산량이 많이 소요되고 암호에 사용되는 라운드 함수를 안전하게 설계해야 한다는 단점이 있다. SPN 구조와 함께 자주 비교된다. 대표적인 암호로는 DES가 있고, SingleDES는 안전성 문제로 사용하고 있지 않다.
- 두 개의 라운드를 갖는 파이스텔 구조 및 동작 과정 예시
- 라운드 키 두 개는 각각 K1, K2이며, 키는 암호화와 복호화에서 역순으로 사용된다.
- 두 개의 믹서는 서로 역관계이고, 스와퍼는 서로 역관계이기 때문에 암호화 알고리즘과 복호화 알고리즘은 서로 역관계이다.
- 전송 도중 암호문은 변동되지 않았다면, L4=L3와 R4=R3를 만족한다는 가정하에 L6=L1과 R6=R1이라고 증명할 수 있다.
장점
형태보존암호의 주된 장점은 작은 크기의 평문을 암호화할 수 있다는 것이다. 하지만 만약 평문의 크기가 작다면, 출력될 암호문의 크기 또한 작기 때문에 안전성에 큰 문제가 생길 수 있는데, 이를 형태보존암호는 추가 정보인 트윅(Tweak)을 사용해서 안전성을 확보한다. 예를 들자면 16자리 신용카드번호를 암호화한다고 할 때, 신용카드 앞의 6자리와 마지막 4자리는 신용카드 회사의 정보나 변경되지 않아야 할 정보가 담겨 있기 때문에 중간의 6자리만을 암호화한다. 따라서 평문은 가지, 즉 100만 가지 경우의 수가 존재한다. 만약 모든 데이터베이스에 개의 카드번호가 있다면 그중에서 약 100개는 중간 6자리가 같은 숫자로 이루어져 있다. 만약 중간 6자리가 동일한 카드 번호를 같은 트윅을 암호화한다면 모두 같은 암호문이 된다. 하지만 가운데 6자리를 제외한 나머지 카드값을 트윅으로 사용한다면 서로 다른 암호문을 가지게 된다.
형태보존암호는 평문과 암호문이 같은 형태이기 때문에 둘의 크기도 동일하기 때문에, 일반적인 블록 암호에서 상대적으로 긴 길이의 암호문을 전부 저장할 필요는 없다. 신용카드의 16자리 10진수 번호 중에서 일부 6자리를 암호화해야 한다고 할 때, 만약 128비트 블록 사이즈의 블록 암호 AES를 이용해서 암호화한다면 암호문의 길이도 128비트가 될 것이다. 평문인 6자리 10진수는 이므로 약 20비트 밖에 안 되는데, 암호문은 이보다 6배 이상 큰 128비트 길이를 갖는다. 따라서 신용카드를 담당하는 회사에서 모든 카드 번호를 암호화해서 저장한다면, 평문을 저장한 데 비해서 암호문을 저장하는데 필요한 저장 용량은 6배 이상이 된다. 하지만 여기서 형태보존암호를 사용한다면 말이 달라진다. 형태보존암호를 사용하여 6자리 10진수 신용카드 번호를 암호화하면 암호문도 마찬가지로 6자리 10진수가 된다. 따라서 평문 대신에 암호문을 저장하기 위한 추가적인 저장 용량은 필요하지 않게 된다.
형태보존암호은 기존의 시스템에서 이용하고 싶을 때 시간과 비용 면에서 부담을 덜 수 있다. 개인정보와 거래정보 등 각종 정보를 지금까지 한 번도 암호화를 하지않고 관리해온 시스템을 갖고 있는 기업이 있다고 가정한다. 암호화가 안 되어 있는 그 정보들을 정부의 정책이나 다른 모종의 이유로 암호화를 해야 하게 될 경우, 이 기업에서 사용하고 있던 시스템은 평문의 형태에 맞춰서 작동하고 있었기 때문에 암호문의 형태에 맞춰서 시스템이 운용될 수 있도록 주변의 모든 시스템을 교체하거나 수정해야만 한다. 시간과 비용면에서 상당한 부담이 되는 과정이기 때문에 기업 입장에서는 당연히 부담스러울 수밖에 없다. 그러나 여기서 형태보존암호를 적용한다면 기존의 시스템을 크게 바꿀 필요 없이 그대로 사용할 수 있다. 기존의 시스템을 수정하거나 교체할 필요가 없어서 시간과 비용 면에서 부담을 덜 수 있다.[4] 형태보존암호 방식의 대표적인 예로 블록 암호 운영 모드를 이용한 방식을 들 수 있는데, 암호화 메시지 저장을 위해 별도로 추가적인 저장 공간을 확보할 필요가 없으며, 기업은 시스템 변경 최소화로 인한 암호화 시스템 구축 비용의 절감 효과를 얻을 수 있다. 이 운영모드는 2016년에 미국 국립표준기술 연구소에서 관련 표준을 제정하였으며, 국내의 대표적인 형태보존암호로는 FEA가 있다.
비교
- 블록 암호 : AES, DES 등 기존의 블록 암호화 기술은 이진 데이터가 암호화 대상이기 때문에, 이를 이용해서 주민등록번호나 신용카드번호를 암호화하면 형태가 달라진다. 신용카드 1234567898765432를 AES로 암호화하면 원본과 다른 형태의 암호문이 출력된다. 1234567898765432를 숫자로 가정하고 AES로 암호화하면 16자리보다 더 큰 수가 출력될 가능성이 높다. 1234567898765432를 아스키코드로 가정한 후 AES로 암호화한다면 그 결괏값의 길이가 원본과 달라질 수 있으며, 아스키코드의 숫자 범위인 0x30~0x39의 사이에서 값이 출력될 가능성도 낮아진다.
- 토큰화 : 형태보존암호와 토큰화 기술을 비교했을 때 토큰화가 가지는 특징은 다음과 같다. 토큰화는 임의로 생성된 값, 즉 토큰을 신용카드번호와 주민등록번호처럼 민감한 정보 대신 사용하는 기술을 말한다. 실제로 민감한 정보는 안전한 곳에 따로 보관되며 토큰과 실제 데이터를 연결하는 매핑 테이블이 필요하다. 토큰과 실제 데이터와의 연관성이 없기 때문에 공격자가 토큰에서 실제 데이터를 유추하는 것 자체가 불가능하다. 또, 토큰화 시스템의 구축과 데이터 분리 보관, 실시간 토큰 동기화 등 추가적으로 보안과 관련한 부담이 생기며, 시스템의 개발과 유지에 비용이 든다.[2]
라이브러리
파이썬, C 언어, C++, 자바 등 다양한 플랫폼 기반의 형태보존암호 관련 오픈 소스 라이브러리가 존재한다.[2]
라이브러리 설명 라이선스 LibFTE 파이썬 기반의 FFX(FF1) 라이브러리 MIT libffx 파이썬 기반의 FFX(FF1) 라이브러리 GPL botan(FPE) C++ 기반의 FE1 라이브러리 BSD2 Miracl C/C++ 기반의 BPS 라이브러리 상업 라이선스 및 AGPL DotFPE .net 기반의 FE1 라이브러리 NewBSD 자바FPE 자바 기반의 FE1 라이브러리 NewBSD
종류
형태보존암호 기법은 prefix cipher, cycle-walking cipher, VFPE, FF1, FF3-1, FEA, Mix-and-cut, Swap-ornot, Sometimes-recurse-shuffle 등이 있다. 이러한 다양한 기법 중 FFX, VAES3, BPS는 각각 FF1, FF2, FF3라는 명칭으로 미국 국립표준기술 연구소의 표준에 제정되었다. 하지만 FF2는 안전성 문제가 제기되어서 표준에서 삭제되었고, 현재 FF1과 FF3만 표준으로 사용되고 있다. 형태보존암호 기법 중에서도 블랙과 로가웨이가 도메인의 크기별/알고리즘의 복잡도별로 제안한 세 가지 방법인 prefix cipher, cycle-walking cipher, generalized-Feistel cipher은 여러 형태보존암호의 근간이 되었다.[2]
- FF1, FF3
- FF1과 FF3은 둘 다 AES 같은 기존의 블록 암호를 파이스텔 구조와 함께 적용해서 암호화한다. 임의의 평문 길이에 모두 적용할 수 있는 파이스텔 구조의 형태보존암호이다. 내부 F 함수로 일반 블록 암호를 사용하며, 매 라운드에서 법 연산을 취해서 평문의 길이를 유지한다. 두 기법은 파이스텔 구조의 라운드 수와 입력되는 트윅의 길이, 평문이 입력되는 순서 등에서 차이점이 존재하는데, 예를 들어 FF1은 1평문이 입력되는 그대로 사용하며 10라운드를 사용한다. 반면에 FF3은 평문이 역순으로 입력되어야 하고, 8라운드를 사용한다. FF1, 즉 FFX를 제안한 벨레어(Bellare)는 FF1과 FF3에 대해 새로운 복구 공격을 제안했고 이들에게 취약점이 있다고 말했었다. 메시지 복구 공격은 파이스텔 구조에서 오른쪽 절반 값이 동일한 서로 다른 두 입력값에 대해서, 두 초깃값의 왼쪽 절반 연산과 출력된 값들의 왼쪽 절반 연산을 비교한다. 이때 라운드 수가 크지 않다면 초깃값과 출력값의 연산 결과가 같은 확률이 높다는 성질을 기반으로 공격한다. 결론적으로 FF1과 FF3가 고정된 라운드 수를 수행하면 크기가 작은 평문에 대해 메시지 복구 공격에 약할 수도 있다.[4]
- prefix cipher
- prefix cipher은 형태보존암호를 적용하려는 도메인이 {0,...,N-1}처럼 정수로 주어졌을 때, 해당 도메인에 속하는 각각의 정수에 AES, DES와 같은 블록 암호 알고리즘을 사용해서 의사난수 가중치를 계산하여 정렬하는 방법이다. 모든 평문에 대해서 임의의 블록 암호를 사용하여 암호문을 얻은 다음 오름차순으로 정렬한 후, 다시 복호화한 것을 제일 처음의 평문들의 prefix cipher 암호문으로 대응시킨다. 알고리즘이 간단하고 도메인 크기가 작은 경우에 용이하다는 장점이 있다. 그러나 한 번 암호화할 때마다 평문의 크기만큼 암호화를 하고 정렬해야 하는 불편함이 있어 효율적인 방식은 아니다. 만약 도메인의 크기가 커진다면 매핑 테이블의 크기 또한 커져서 저장과 사용이 번거롭다.
- cycle-walking cipher
- cycle-walking cipher은 블록 암호화 알고리즘을 사용하여 원본과 동일한 형태의 결과가 나올 때까지 알고리즘을 계속해서 수행하는 방식을 말한다. 앞의 prefix-cipher와는 달리 전체 매핑 테이블을 유지할 필요가 없다. 언젠가 알고리즘이 종료되는 것은 맞지만, 알고리즘을 수행할 때 그 알고리즘이 언제 종료하는지 시간을 예측할 수 없다. 사용하는 블록 암호보다 원하는 형태의 크기가 작을 때 반복 횟수가 많이 증가할 수도 있어 다소 위험하다. 원본 형태의 허용 범위가 작을수록 지나치게 많은 반복으로 인해 실용성이 떨어지며, 허용 범위 값의 범위가 블록 암호화 알고리즘의 고정된 블록 크기에 영향을 받는다.
- generalized-Feistel cipher : 파이스텔 네트워크를 이용한 방법으로, 각 라운드의 보조키로 블록 암호화 알고리즘의 출력을 사용하여 형태보존암호를 수행한다. 원본 형태와 다른 출력이 발생하면 cycle-walking과 유사하게 원하는 형태가 얻어질 때까지 파이스텔 네트워크를 반복해서 수행한다. prefix-cipher와 cycle-walking cipher와 달리, 도메인의 크기가 큰 경우에도 비교적 큰 성능 저하 없이 사용할 수 있기 때문에 실무에서 많이 사용되며, 여기에 기반한 다양한 알고리즘이 제안되었다. 대부분의 형태보존암호는 prefix cipher와 cycle-walking cipher, generalized-Feistel cipher를 기반으로 만들어지기 때문에 동일한 안전 정도를 보장한다.
- VFPE
- VFPE는 ISA 카드회사에서 채택한 형태보존암호로, 카운터 모드를 사용한다. 각 카운터에서 얻은 블록 암호의 암호문에 법 연산을 취하여 원하는 형태의 암호문을 얻는 방식이다. 예를 들어 카드번호인 16자리 10진수의 암호문은 16개의 카운터에서 얻어진 블록 암호의 암호문들에 각각 법 10 연산을 취해서 얻을 수 있다.
- FEA(Format-Preserving Encryption Algorithm): 국가보안기술연구소에서 개발한 형태보존암호기술로, 국내에서 독자적으로 개발했다. FF1과 FF3와 달리 내부 F 함수로서 FEA 함수를 사용한다. 그리고 F 함수의 길이를 조정해서 평문의 길이를 유지한다. 미국 국립표준기술 연구소에서 개발한 FPE의 파이스텔 구조와 다른 트위커블 가변길이 블록 암호의 특징을 갖는다. 국내에서 사용중인 민감한 개인정보들의 길이가 대체로 짧다는 것을 토대로 고안되었다. FRA는 기존의 AES와 달리 원본 데이터에 대해서만 암호화하는 특징을 갖고 있어, 암호화 솔루션의 구축비용은 감소하고 성능은 향상할 수 있는 암호화를 할 수 있다. 형태보존암호가 실용화된다면 암호화에 있어서 기존 데이터베이스의 스키마를 변경할 필요가 사라진다는 장점이 있다. 형태보존암호에서 평문의 길이가 짧다면 라운드 수를 증가하는 방식을 적용해서 비용면에서 큰 부담이 들지 않기 때문에 메시지 복구 공격에 충분한 안전성을 확보하는 기법 등 다양한 방법에 관해서 연구 중이다.[5]
표준화
ISO에 등재되는 암호기법들이 표준화되기 위해서는 필요성과 적합성을 모두 적합해야 한다. 여러 분야에서 자체적으로 사용되고 있는지와 산업계의 요구 등을 충족해야 하며, 보통 최소 3년 정도의 국제적인 공개검증 기간을 진행해야만 한다. 따라서 형태보존암호의 표준화는 쉬운일이 아니다.
형태보존암호의 표준화는 산업계의 요구에서 시작되었다. 산업체의 요청으로 형태보존암호 표준화 필요성이 대두되었다. 2017년 10월에 진행된 제55차 ISO/IEC JTC1 SC27 국제 표준화 회의에는 한국대표단도 참여했었다. 한국대표단은 회의에서 FEA를 소개하며 산업계의 형태보존암호 표준화 요청에 따라서 표준화의 필요성을 제시했다. 제시된 내용에 따라 형태보존암호의 필요성과 적합성을 검토하기 위해 SP 절차를 시작했으며, SP에는 한국의 송정환 교수와 미국의 릴리 첸이 참가했다. 하지만 이 이후에 형태보존암호에 대한 의견은 한국과 미국을 제외하고는 많지 않은 편이었고, 결국 2018년 4월 중국에서 열리는 제56차 ISO/IEC JTC1 SC27 국제표준화 회의에서 각국의 전문가들에게 구체적인 질문을 남기기 위해 SP를 연장했다. 이후 한국에서는 FEA-2를, 미국에서는 미국 국립표준기술 연구소 표준 형태보존암호인 FF1과 FF3을 표준화 후보 알고리즘으로 제안했다. 그러나 형태보존암호가 작은 정의역을 갖는다는 특성을 기반으로 한 키 복구 공격과 코드북 공격 등 다양한 안전성 검증 절차를 진행한 결과, 프랑스와 러시아는 형태보존암호의 안전성이 우려된다는 의견을 제시했다. 이에 작은 정의역 특성을 이용한 공격들에 대한 논의를 위해서 SP 기간을 또 6개월을 늘려 연장전을 진행했다. 작은 크기의 정의역을 이용한 공격은 상당히 효과적이라 미국의 FF3은 코드북 공격으로 완전히 깨졌다. FF1과 FEA-2도 안전성 분석에서 뛰어난 결과를 보여주지 못했고, 형태보존암호는 작은 정의역을 갖는다는 특성을 이용한 공격에 대응하기 위해 정의역의 최소 크기에 대한 제한이 필요하다는 의견이 나왔다. 의견에 따라, 작은 크기의 정의역을 이용한 공격에서 FEA-2는 정의역의 크기가 218 이상일 때 안전하다는 결론이 나왔는데, 이는 18비트 길이로 약 5자리 10진수가 되는 상당히 짧은 길이에 해당한다. 반면에 미국의 FF1, FF3은 FEA-2와 동일한 조건에서 32비트 길이의 정의역 크기가 필요하다는 결과가 나왔다. 특히 FF3은 코드북 공격으로 완전히 깨진 상황에서 알고리즘을 수정해야 했고, 결국 FF3을 FF3-1로 수정해서 2019년 12월 28일에 미국 국립표준기술 연구소 800-38G revision 1 이라는 문서를 발행했다. 2019년 4월에 이스라엘에서 열린 제 58차 ISO/IEC JTC1 SC27 국제표준화 회의에서 러시아와 프랑스는 함께 형태보존암호의 안전성 분석에 대해서 아직 충분히 논의되지 않았기 때문에 표준화를 시작하기에는 시기가 이르다고 의견을 제시했다. 형태보존암호에 대한 공격이 비교적 적었으며, 발표된 논문들이 모두 2016년에서 2018년 사이에 몰려있기 때문이다. 따라서 SP 기간이 6개월 더 연장되었다.[4]
각주
- ↑ 정수용, 홍도원, 서창호, 〈[메시지 복구 공격에 안전한 형태보존암호]〉, 《한국정보과학회》, 2017-08
- ↑ 2.0 2.1 2.2 2.3 송지환, 〈민감 정보 암호화에 따른 형태 보존 암호화 기술의 재조명〉, 《소프트웨어정책연구소》, 2016-05-25
- ↑ 김영기, 〈[금융부문 암호기술 활용 가이드]〉, 《금융보안원》, 2019-01
- ↑ 4.0 4.1 4.2 송정환, 〈[형태보존암호는 필요한가?]〉, 《ICT스탠다드위클리》, 2019-06
- ↑ 임지환, 나관우, 우재민, 서화정, 〈형태보존암호화를 이용한 랜섬웨어 방지 및 스테가노그래피 보안 강화기술 〉, 《한국정보통신학회논문지》, 2018-05
참고자료
- 형태보존암호 위키피디아 - https://en.wikipedia.org/wiki/Format-preserving_encryption
- 송지환, 〈민감 정보 암호화에 따른 형태 보존 암호화 기술의 재조명〉, 《소프트웨어정책연구소》, 2016-05-25
- 정수용, 홍도원, 서창호, 〈[메시지 복구 공격에 안전한 형태보존암호]〉, 《한국정보과학회》, 2017-08
- 임지환, 나관우, 우재민, 서화정, 〈형태보존암호화를 이용한 랜섬웨어 방지 및 스테가노그래피 보안 강화기술 〉, 《한국정보통신학회논문지》, 2018-05
- 김영기, 〈[금융부문 암호기술 활용 가이드]〉, 《금융보안원》, 2019-01
- 송정환, 〈[형태보존암호는 필요한가?]〉, 《ICT스탠다드위클리》, 2019-06
같이 보기

 위키원
위키원