톱니바퀴를 이용한 수동계산기
톱니바퀴를 이용한 수동계산기란 1645년 수학자이자 과학자인 블레즈 파스칼(Blaise Pascal)이 톱니바퀴의 원리를 이용하여 만든 최초의 기계식 수동계산기이다. 그 당시에 덧셈, 뺄셈이 가능하였으며 오늘날 컴퓨터의 발명의 표본이 되는 기술이다. 흔히 파스칼 계산기(Pascal's calculator), 파스칼린(pascaline) 이라 부르고 라이프니츠가 만든 계산기도 톱니바퀴를 이용하여 만들었다.
파스칼 계산기[편집]
블레즈 파스칼(Blaise Pascal)은 프랑스인으로 수학, 과학, 철학가로 그 당시 세금을 계산하는 공무원이었던 아버지의 밑에서 어린 시절을 보내게 되었다. 오늘과 같이 전자계산기가 있는 것도 아니고 오로지 사람의 수작업에 의지했기 때문에 세금을 계산하는데 하나하나 글을 작성하며 계산을 했고, 이에 오랜 시간이 소요되고, 실수라도 하면 큰 피해가 있었기에 수많은 검산과 노력이 필요했다. 파스칼은 어린 시절 밤늦게까지 세금계산으로 고생하시는 아버지의 모습을 보며 기계를 사용하여 더욱 편하게 계산을 하는 장치에 대한 발명을 키워왔다. 이로 인해 파스칼은 톱니바퀴를 사용하여 만든 최초의 수동식 계산기를 만들게 되었다. 여러 개의 톱니바퀴를 맞불려서 돌아가게 되고 0~9까지 10진수의 기법을 사용하여 십만 자리까지 계산을 사용할 수 있었다. 오늘날 계산기와는 다르게 덧셈과 뺄셈, 자리 올림기능까지만 사용할 수 있었다. 일의 자리를 나타내는 톱니바퀴가 시계방향으로 1회전 하면 숫자 1이 올라가고 9에서 10으로 가는 경우에는 십의 자리 숫자가 1이 올라가고 일의 자리는 다시 0부터 시작하게된다. 십진수 기법을 사용하여 톱니바퀴 한 단위 1/10을 회전 하는 방식으로 가산기로 만들어 졌다. 다이얼에 의하여 십진수를 표시하는 6개의 원판이 두 개로 이루어져 있고, 각 원판에는 0부터 9까지의 십진수가 적혀 있어 유리를 통해 한 번에 하나의 숫자만 볼 수 있도록 설계가 되었다. 다이얼을 이루는 두 개의 집합은 각 수를 기억하는 레지스터(register)로 사용되었고 하나의 레지스터는 계산 결과를 누적하는 누산기(accumulator)의 역할을, 다른 하나는 누산기에 더하거나 빼는 값을 저장하는 데 사용되었다. 파스칼은 1645년에 처음으로 자신이 만든 기계를 대중에 공개하기 전까지 50개의 시제품을 만들어 시험해 보았고 이후 10년 동안 기계를 계속 개선해나가면서 약 20 여개를 더 만들어 냈다. 파스칼은 자신이 만든 계산기에 대한 자부심과 함께 계산기의 장점을 부각했다. 파스칼은 톱니바퀴를 사용하여 굉장히 정교하고 케이스를 사용함으로 튼튼하고 내구성이 우수하다고 주장했다. 기계의 견고함에도 불구하고 바퀴가 손으로 작동하기 때문에 움직일 때 편하고 계산은 간단하고 빠른 특징을 가지고 있다. 게다가 톱니바퀴를 이용한 수동계산기는 실수의 위험이 존재하지 않기에 완벽에 가까워 보였다 하지만, 수동계산기는 일을 능률적으로 처리할 수 있었지만, 덧셈과 뺄셈이외의 연산은 할 수가 없다는 단점 때문에 큰 관심을 끌지 못했다. 하지만 톱니바퀴를 이용한 수동계산기의 탄생은 점차 유럽을 시작으로 하여 전 세계적으로 기계식 수동 계산기 개발을 촉발하는 계기가 되었고 훗날 라이프니츠의 계산기가 탄생하게 되었다. 이는 오늘날의 컴퓨터의 모델이 되는 제품이다. 파스칼이 발명한 이 계산기는 구두 상자 정도로 작은 크기였지만 계산기 발달에 세 가지 원칙을 세웠다. ‘첫째자리 올림은 자동으로 수행해야 한다.', '둘째 뺄셈은 다이얼을 역으로 회전시킴으로 가능하다.', 셋째 곱셈은 덧셈의 반복적인 수행으로 가능하다.’ 이고, 현재에도 이 세 가지 원칙은 많은부분에서 사용되고 있다. 오늘날에는 20여 대의 기계 중에서 수동계산기 9개만이 현존하고 있다.[1][2]
작동원리[편집]
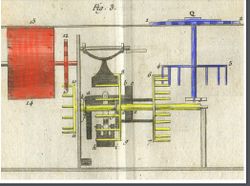
수동계산기의 내부를 보면 크게 세 가지로 나뉘게 되는데, 값을 입력하는 입력 다이얼(input dial)과 값을 계산하는 처리 장치(add, carry mechanism)와 출력값을 실린더에 보여주는 넘버 휠(number wheel)로 나누어진다. 옛날 전화기를 보면 다이얼을 돌려서 원하는 번호를 입력하는 원리가 톱니바퀴를 이용한 수동계산기에서 왔다. 또한 일상생활 속에서 카지노 룰렛의 원리와 비슷하다. 원하는 값을 얻기에 입력 다이얼을 돌려서 값을 지정한다. 그 다음 입력 다이얼과 연결된 톱니바퀴가 내부의 처리를 담당하는 메커니즘과 맞물려서 돌아가게 되고 출력값을 담당하는 실린더는 처리 톱니바퀴의 회전에 의해 그 값이 결정된다. 입력 다이얼과 맞물리는 톱니를 크라운 휠(crown wheel)이라 하고 바로 맞은편에 있는 톱니바퀴는 누산기의(accumulator) 역할을 한다. 누산기의 역할을 하는 톱니에 멈춤 쇠(backstop pawl)가 달려있어 일정한 값을 지정하는데 오차 없이 계산값을 출력하게 해준다. 예를 들어 룰렛의 같은 경우 룰렛이 돌아가다가 어떠한 영역에 멈춰야 하는데 그때 멈춤 쇠로 인해 특정 값에 멈추게 된다. 이같이 톱니바퀴를 이용한 수동계산기에도 입력 휠을 통해 값을 돌릴 때 정확한 값이 실린더에 나오도록 역할을 한다. 누산기의 역할을 하는 톱니바퀴에 추가적으로 작은 톱니바퀴 하나를 더 붙인다. 이는 출력값이 지정되는 실린더와 맞물려서 실린더가 회전하게 되고 1개의 톱니가 회전을 할 때마다 값이 달라진다. 실린더는 톱니의 거리에 따라 맞게 0부터 9까지의 숫자가 적혀있다. 실린더에 붙어있는 작은 톱니바퀴를 피니언(pinion)이라 한다. 옆의 그림에서 보면 파란색 톱니바퀴가 입력 다이어, 노란색 톱니바퀴 부분이 누산기의 역할을 하고 빨간색 실린더는 출력값을 보여준다. 실린더 바로 오른쪽에 있는 멈춤쇠도 볼 수 있다. 톱니바퀴를 이용한 수동계산기는 9의보수 즉 10진법을 사용한다. 때문에 0부터 9까지 숫자를 표현할 수 있다. 9에서 0으로 될 때에는 입력 다이얼 톱니바퀴의 붙어있는 소트오르를 사용하여 바로 윗자리의 숫자를 넘겨주는 역할을 한다. 예를 들어 35+47을 계산한다고 하면, 초기의 값을 0으로 모두 맞춘다. 기본값에 35를 지정해주고 그다음 3을 4칸만큼 시계방향으로 움직여 7로 만들어준다.5+7=12 이기에 십의 자리가 반환됨으로 일의 자리 다이얼을 5칸 움직여 2로 만들어준다. 그러면 운반 메커니즘에 의해 소트오르가 움직여 십의 자리 실린더를 8로 만들어 준다. 그러므로 올바른 값인 82가 나오게 된다. 뺄셈은 이와 반대로 모든 실린더의 값을 9로 맞추어주고 출력값이 두 가지가 존재하는데 수평 슬랫을 밑으로 내리면 된다. 그다음 덧셈과 같이 시계방향으로 원하는 값만큼 다이얼을 돌려주어 계산 하면 된다.- 운반 매커니즘
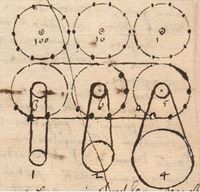
- 톱니바퀴를 이용한 수동계산기의 운반 메커니즘은 소트오르(sautoir)이다. 옆의 그림을 보면 자세히 나와 있다. 하나의 바퀴에 갈고리 모양으로 멈춤 쇠가 달려있다. 옆의 바퀴는 입력 바퀴와 연결된 톱니바퀴이다. 만약 19에서 20으로 값이 변한다면 십의 자리 숫자를 2로 바꾸어 주어야 한다. 오른쪽 톱니바퀴를 보면 파란색 점(carry pin) 두 개가 있다. 소트오르는 입력 다이얼 톱니바퀴와 맞물려 있음으로 캐리 핀이 회전하여 멈춤 쇠를 서서히 올리게 되고 일의자리 숫자가 0에서 9로변환이 될 때 멈춤 쇠가 내려가게 되어 올림 차수를 해내게 된다. 꼭 일의 자리뿐만 아니라 어떠한 자리수에도 해당이 된다. 소트오르의 멈춤 쇠가 내려갈 때의 작용의 힘으로 숫자가 옆의 톱니바퀴의 1개의 톱니만큼 값이 변하게 된다.
- 9의보수
파스칼 계산기는 10진수 즉 9의보수의 값을 사용했기 때문에 0에서 9까지의 값만 표현되고 10이 되는 순간에 값을 윗자리수를 넘겨준다. 공식으로 나타내면 한자리 십진수 숫자의 보수는 X-a 이다 9의보수를 사용하니 9-a가된다. 예를 들어 9의 6의 보수는 3이된다. C9(a)= 9-a C9(6)= 9-6=3 이다. 따라서 10진수 기계에서의 보수는 C9=10의 N승-1-a이다. C9(a-b)=10^n-1-a , C9(a-b)=10^n-1-(a-b) C9(a-b)=10^n-1-a+b C9(a-b)=C9(a)+b
라이프니츠 계산기[편집]
파스칼에 의해 덧셈과 뺄셈이 가능한 톱니바퀴 계산기의 출현으로 능률적인 계산이 가능해졌지만 파스칼린은 덧셈과 뺄셈 이외의 연산은 불가능하다는 단점이 있었다. 이러한 단점을 보완하기 위해 독일의 수학자 빌헬름 라이프니츠(Wilhelm Leibnitz)는 곱셈과 나눗셈까지 가능한 사칙연산 계산기를 발명했다. 라이프니츠가 발명한 계산기는 파스칼이 발명한 파스칼린과 똑같은 톱니바퀴 방식이지만, 스텝 실린더(stepped cylinder)라는 9개의 기어들을 사용했다. 각각의 9개의 기어는 그 크기가 다르고, 보다 작은 기어들이 그 위에 위치해 있으며 각각의 기어들은 곱셉의 값을 나타내는 피승수를 표시하고 기어의 대응되는 숫자에 적용되도록 위치시켰다. 실린더를 통해 값을 지정하게되면 1회 회전은 일단 곱셈의 결과로 기록되고 다른숫자는 크기가 더 큰 기어들의 회전수로 표시되도록 하였다. 라이프니츠의 계산기는 완벽하게 작동했지만 올림과 받아 내림을 완벽하게 자동화시키지는 못했다.[4] 곱셈과 나눗셈은 말 그대로 덧셈과 뺄셈을 여러번 반복하고 숫자를 추가하면된다. 하지만 이 경우에는 같은숫자를 추가하고 빼는과정에서 배수가 필요하며 반복되는 숫자 저장과 계산방법, 반복횟수에 대한 메커니즘이 복잡해진다. 라이프니츠는 단순히 여러번 더해서 곱셈을 하는것이 아닌 곱셈과 나눗셈의 메커니즘을 적용하여 계산기를 만들었다. 1672년 라이프니츠는 전송코드가 있는 개념을 설명했다. 맨윗줄은 파스칼 계산기이고 맨아래는 곱셈기이다. 곱셈의 경우 365 × 124를 할 경우에 먼저 365에 4를 곱한다. 여기에 4라고 표시된 더 큰 지름의 원반은 모든 가운데'바퀴가 4 번 회전하므로 결과는 1,460이 나오게된다. 그 후, 기계의 하단 두 줄 365 × 20 연산을 실행하려면 왼쪽으로 이동해야한다. 결과적으로 7,300이된다. 이전값과 더하고 마지막으로 365 × 100을 하게되면 최종 결과 인 45,260을 얻게된다. 이 방식으로 곱셈을 하고 라이프니츠는 황색 황동 계산기를 구현했다. 톱니바퀴는 이빨모양과 비슷한 움푹 패인 바퀴를 사용했다. 라이프니츠는 단계별 계산방법(Step Reckoner)을 사용하여 톱니바퀴 모양도 계단식으로 정립하고 앞서 말했듯이 곱셈방식에 있어 단계별로 수행하는 기술을 사용하였다. 십진법을 사용하여 라이프니츠는 체계적으로 글로 계산하는 것에서 톱니와 함께 크기가 다른 10 개의 체인 톱니바퀴가있는 원통형 롤러에 수행되는 기계적인 계산 과정으로 단일 단계의 해결방안을 제시했으며 곱셈은 반복 덧셈으로 수행되고 나눗셈은 계속 뺄셈으로 수행되었다. 각각의 산술 연산의 결과는 작은 원형 디스크에서 읽을 수 있다. 1673년 런던의 왕립 학회를 통해 라이프니츠의 계산기가 소개가되고 점자 보급이되기 시작했다. [5] 또한 라이프니츠는 이진수 발명하였는데 이는 오늘날 컴퓨터에 사용되는 가장중요한 원리가 되었다. 라이프니츠가 만든 계산기는 당시 제조기술은 뛰어났지만 운반메커니즘의 결함으로 기계가 거의 작동되지 않았다. 두 개의 표준모델이 제작되었고 오늘날에는 독일 하노버의 국립 도서관에 한 개만 남아있다. 단계별(계단식)로 계산의 결함에도 불구하구 미래에 많은 계산기 제작자들에게 영향을 끼치게 되었다.[6] 이후에도 찰스 배배지(Charles Babbage)가 만든 차분기관, 해석기관도 톱니바퀴를 사용하여 만들었다.
인물[편집]
각주[편집]
- ↑ 정영애 교수, 〈파스칼 라인(Pascal line)〉, 《전국과학관길라잡이》,
- ↑ ,〈[http://www.bibnum.education.fr/sites/default/files/pascal-analysis-en-new.pdf The Pascaline, the “machine that relieves the failure of memory” ]〉, 《bibnum》,
- ↑ Mechanical Computing, 〈How the Pascaline Works〉, 《유튜브》, 2012-03-10
- ↑ 정영애 교수, 〈계산기(calculating machine)〉,《전국과학관길라잡이》,
- ↑ Florin-Stefan Morar,〈Reinventing machines: The transmission history of the Leibniz calculator〉, 《ResearchGate》, 2014-03
- ↑ 〈Leibniz Calculating Machine〉, 《hannover》, 2019-01-04
참고자료[편집]
- 정영애 교수, 〈파스칼 라인(Pascal line)〉, 《전국과학관길라잡이》
- 정영애 교수, 〈계산기(calculating machine)〉,《전국과학관길라잡이》,</ref>
- 〈The Pascaline,the “machine that relieves the failure of memory”〉, 《bibnum》
- Mechanical Computing, 〈How the Pascaline Works〉, 《유튜브》, 2012-03-10
- Florin-Stefan Morar,〈Reinventing machines: The transmission history of the Leibniz calculator〉, 《ResearchGate》, 2014-03</ref>
- 〈Leibniz Calculating Machine〉, 《hannover》, 2019-01-04
같이 보기[편집]

 이 톱니바퀴를 이용한 수동계산기 문서는 컴퓨터에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.
이 톱니바퀴를 이용한 수동계산기 문서는 컴퓨터에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

 위키원
위키원