머클경로

머클경로(Merkle path)는 어떤 거래의 진위를 따질 때 이를 검증하는 과정을 말한다. 머클루트가 주어진다면, 더 쉽게 검증할 수 있다.

개요

머클경로는 풀노드로부터 정보를 받아 해시함수에 대입 시켜 사용자가 해시 값의 상대값을 알아가면서 계속 해시를 진행해 나갈 수 있게 하는 것이다.

머클트리

머클트리

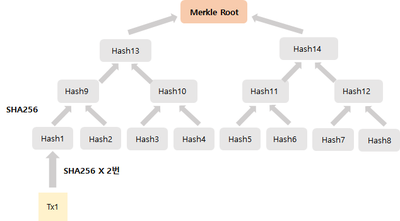
머클트리는 ‘트리구조’를 형성하고 있는 암호화 과정이라고 할 수 있다. 꼭대기에 위치한 최종 값을 '루트', 하부의 값들을 '리프'라고 칭한다. 8개 거래에 대한 머클트리를 예로, 위 그림과 같이 거래에 대한 해시값이 Hash1부터 Hash8과 같이 '리프'가 이어져 있고, 이를 두 개씩 묶어 더한 후 같은 방식으로 진행하여 최종 값인 머클루트를 얻는다. (Hash9 값은 (Hash1 + Hash2)의 sha256 해시를 2번 취한 값 )

머클루트(Merkle Root)란, 단어 속 ‘루트(root)’에서 알 수 있듯이 뿌리와 같은 결과로써 하나의 최종 값을 의미하며, 그림상으로는 맨 위에 해당하는 값이 된다.

이 트리를 보면서 거래가 홀수일 경우에 대하여 의문이 생길 수 있다. 이러한 경우 맨 마지막 거래를 복사하여 거래를 짝수개로 만들어 사용하는 원칙으로 이용되고 있다. (이러한 경우를 균형트리(balanced tree))

머클트리를 보면서 거래의 원본이 그대로 저장이 안 되고 해시값을 이용하는 것에 필요성을 느끼지 못할 수 있지만, 해시의 쓰임새를 다시 한번 생각해 봤을 때, 위변조를 한 번에 알 수 있다는 장점이 있기에 머클루트는 매우 중요하다. 즉, 블록 안의 300개의 데이터 중 1개의 데이터, 혹은 그 1개의 데이터 중 글자 하나만 바뀌어도 해시값인 머클루트는 완전히 다른 값이 나온다는 것을 인지한다면 머클루트의 효과를 확실히 알 수 있을 것이다. (참고로 이더리움의 경우, 머클패트리샤 트리(Merkle-Patricia tree(trie))를 이용하여 '상태(state)'의 정보를 저장한다)

머클트리의 장점은 위변조 가능성을 넘어서, 빠른 탐색을 용이하게 만들어준다. 머클경로를 이용한다면, 머클루트를 알고 있을 때, ‘어떠한 거래가 들어있다는 확인’을 하는 절차는 매우 용이하다. 머클트리에 대해 자세히 보기

예제

머클트리 예시

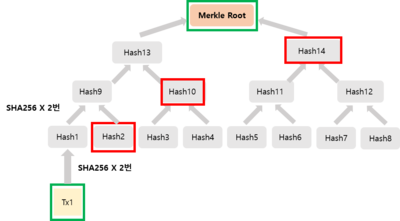
A는 본인의 거래 Tx1이 블록에 담겨있는지 확인하고자 한다면, 풀노드(full-node)로부터 블록헤더와, 머클경로를 전달받는다. 이때, 블록헤더 중 머클루트와 머클경로를 통해 Tx1의 포함 여부를 확인한다. 이어서 Tx1이 들어있다는 것을 확인해야 한다.

Hash2, Hash10, Hash14 만 있으면 머클루트를 직접 계산하여 도출할 수 있다. 즉, A는 Tx1을 이용하여 Hash1을 만들면, 머클경로에 포함된 Hash2를 더하며 Hash9를 얻을 수 있다. 이후 Hash9과 머클경로에 포함되어 있던 Hash10을 통해 Hash13을 얻을 수 있고 같은 방식으로 Hash14를 통해 머클루트를 직접 구할 수 있다. 이 결괏값을 '전달받은 머클루트'와 비교하여 일치한다면 본인 거래 Tx1이 블록에 담겨있다는 것을 확인할 수 있을 것이다. 이는 log2(8)=3개의 머클경로가 포함되어있음을 확인할 수 있다.

이는 SPV(Simplified Payment Verification) 노드가 쉽고 빠르게 특정 거래를 찾을 수 있게 도와준다.

C

머클트리 생성

CBlock::BuildMerkleTree()
{
    uint256 BuildMerkleTree() const
    {
        vMerkleTree.clear();
        // 각 트랜잭션들의 해시값을 따로 저장하여 vMerkleTree 생성
        foreach(const CTransaction& tx, vtx)
            vMerkleTree.push_back(tx.GetHash());
        int j = 0;
        for (int nSize = vtx.size(); nSize > 1; nSize = (nSize + 1) / 2)
        {
            for (int i = 0; i < nSize; i += 2)
            {
            // 만약 트랜잭션이 짝수개가 아니라면, 마지막 트랜잭션의 해시는 자기 자신과 해시
                int i2 = min(i+1, nSize-1); 
             // 트랜잭션의 해시를 2개씩 묶어서 다시 머클트리에 삽입한다.
                vMerkleTree.push_back(Hash(BEGIN(vMerkleTree[j+i]), END(vMerkleTree[j+i]), 
                                           BEGIN(vMerkleTree[j+i2]), END(vMerkleTree[j+i2])));
            }
            // j는 각 트리레벨에 맞춰 삽입해야 할 첫 번째 위치를 가리킨다.
            j += nSize;
        }
        return (vMerkleTree.empty() ? 0 : vMerkleTree.back());
    }
}

위에서 설명한 소스코드를 활용하여 7개의 트랜잭션으로 1차원 벡터(vector)를 구현한다면 아래와 같은 그림이 된다.

• H(tx[0]): 0번 트랜잭션(1번째 트랜잭션)에 대한 해시값
• H(66): 6번 트랜잭션(7번째 트랜잭션)에 대한 해시와 6번 트랜잭션에 대한 해시를 이어붙인 값을 다시 해시한 값

2개씩 묶어서 새로운 해시를 생성해야 하는데 7개의 트랜잭션이므로 홀수개다. 따라서 6번 트랜잭션(7번째 트랜잭션)은 자기 자신과 해시하는 방식으로 구현한다. 2개씩 해시하고 벡터에 삽입하는 과정을 반복하면 벡터의 마지막에는 머클 루트가 자리잡게 된다.

머클트리의 증명

위변조 검사를 할 때 필요한 노드를 추출하는 코드이다. 모든 트랜잭션을 검증할 필요는 없으며, 필요한 트랜잭션 해시들만 선별한다.

// nIndex로 위변조 여부를 검사할 특정 트랜잭션을 선택하고 머클 트리내의 트랜잭션 해시값과 연관된 
// 트랜잭션의 해시들만 따로 추출하여 MerkleBranch를 생성한다.
vector<uint256> GetMerkleBranch(int nIndex) const
{   // nIndex에 해당하는 트랜잭션 증명에 사용되는 노드들을 vMerkleBranch에 담는 작업을 진행
    if (vMerkleTree.empty())
        BuildMerkleTree();
    vector<uint256> vMerkleBranch;
    int j = 0;
    for (int nSize = vtx.size(); nSize > 1; nSize = (nSize + 1) / 2)
    {
        int i = min(nIndex^1, nSize-1); // nIndex^1의 값은 0 또는 1(반복)
        vMerkleBranch.push_back(vMerkleTree[j+i]);
        nIndex >>= 1;
        j += nSize;
    }
    return vMerkleBranch;
}

아래는 위변조를 검사하는 코드이다. 해시할 때의 규칙은 짝수에 해당하는 인덱스를 가진 해시는 다음에 해시될 때 좌측에 위치해야 한다는 것이고 홀수에 해당하는 인덱스를 가진 해시는 우측에 위치해야 한다는 것이다. 즉, SHA256(짝수인덱스를 가진 트랜잭션 해시, 홀수인덱스를 가진 트랜잭션 해시) 이렇게 구성된다는 뜻이다. 해시될 때의 순서에 따라 결괏값은 완전 달라지기 때문에 순서 규칙을 지켜주는 것은 중요하다.

static uint256 CheckMerkleBranch(uint256 hash, const vector<uint256>& vMerkleBranch, int nIndex)
{
    if (nIndex == -1)
        return 0;
    foreach(const uint256& otherside, vMerkleBranch)
    {  // 해시되는 순서를 지켜주기 위해 아래의 두 경우를 구분하여 처리
        if (nIndex & 1) // 트랜잭션의 인덱스가 홀수일 경우
            hash = Hash(BEGIN(otherside), END(otherside), BEGIN(hash), END(hash));
        else            // 트랜잭션의 인덱스가 짝수일 경우
            hash = Hash(BEGIN(hash), END(hash), BEGIN(otherside), END(otherside));
        nIndex >>= 1;   // 해시되는 순서를 맞춰준다.
    }
    return hash; // it should be merkleRoot
}

참고자료

• 에코버스, 〈블록체인상식(17) “머클 트리(Merkle Tree)” - 진위(眞僞)를 판단하는, 작지만 알찬 나무〉, 《네이버 블로그》, 2018-12-24
• Skkrypto, 〈Bitcoin#5: 풀(Pool)과 머클 루트〉, 《브런치》, 2018-11-01
• aeharvlee, 〈비트코인 코어 소스코드로 살펴보는 머클 트리〉, 《미디움》, 2018-06-07
• 세진쨩, 〈머클트리(Merkle tree)에 대해 알아보자〉, 《티스토리》, 2018-10-04

같이 보기

• 머클루트
• 머클트리
• 트랜잭션
• 노드
• SHA-256

이 머클경로 문서는 블록체인 기술에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술 □■⊕, 합의 알고리즘, 암호 알고리즘, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 블록체인 기술 Bech32 • BTP • DRC-20 • EIP • IPFS • KRC-20 • NFT 마켓플레이스 • P2P • P2PKH • P2SH • PFP • PUF • SPV • TPS • TRC-20 • UTXO • 가나슈 • 가명성 • 가스 • 가십 • 가십 프로토콜 • 개념증명(PoC) • 검증가능지연함수(VDF) • 게스 • 고스트 프로토콜 • 공공예산 • 글로벌신뢰인공지능 • 대체가능토큰 • 대체불가토큰(NFT) • 도지더리움 브릿지 • 디지털 자산 • 디지털 희소성 • 라운드 • 라운드 로빈 • 라이트하우스 • 랜덤 • 레그테크 • 레이든 • 리카르디안 계약 • 린스타트업 • 마스터키 • 마스트 • 메인넷 • 멜팅 • 믹싱 • 민팅 • 밈블윔블 • 반감기 • 베타넷 • 변경불가성 • 브릿지 • 블록체인 생태계 • 블록체인 클라우드 서비스(BaaS) • 블룸필터 • 비블록체인 • 비앱 • 비콘체인 • 비트코인코어 • 빤통경제 • 수정 고스트 프로토콜 • 스냅샷 • 스마트 계약 • 스마트 브리지 • 스웜프로토콜 • 스크립트퍼브키 • 스테이킹 • 스텔스 주소 • 스핀오프코인 • 슬래싱 • 시크릿 컨트랙트 • 심플 컨트랙트 • 아토믹스왑 • 암호경제(크립토 이코노미) • 앤드어스체인인공지능 • 앵커링 • 언스테이킹 • 에어드랍 • 에폭 • 오프체인 오더락 • 오피리턴 • 옵코드 • 원토큰 문제 • 웨이 • 위스퍼 프로토콜 • 위임 • 유니스왑 • 유동성 • 이더리움 가상머신(EVM) • 이더리움 클라이언트 • 이중지불 • 익명성 • 인증된 익명 아이디 • 인터레저 프로토콜(ILP) • 자산화 • 잠금 스크립트 • 최소기능제품(MVP) • 컨소시엄 블록체인 • 컬러드코인 • 코인셔플 • 코인소각 • 코인에이지 • 코인조인 • 코인토싱 • 크립토노트 • 키스토어 • 타임락 • 테스트넷 • 토다 • 토큰 이코노미 • 토큰화 • 튜링완전 • 튜링불완전 • 트랜잭션 아이디(TxID) • 트러스트 컨트랙트 • 트루빗 • 트릴레마 • 파워 • 파티셔닝 • 퍼블릭 블록체인 • 페널티 • 프라이버시 • 프라이빗 블록체인 • 플랫폼 • 플러딩 • 피어 • 피투피(P2P) • 하이브리드 블록체인 • 합의 • 해시락 • 해시타임락(HTLC) • 해제 스크립트 • 확장성 해시 레인보우 테이블 • 매핑 • 머클경로 • 머클루트 • 머클트리 • 분산해시테이블(DHT) • 블록해시 • 스큐드 머클트리 • 온라인툴즈 • 이전블록해시 • 카뎀리아 • 해시 • 해시레이트 • 해시맵 • 해시충돌 • 해시테이블 • 해시파워 • 해시함수 • 해싱 블록 고아블록 • 그래핀 • 논스 • 마이크로블록 • 베이킹 • 북키퍼 • 브랜치블록 • 브로드캐스팅 • 블록 • 블록높이 • 블록바디 • 블록생성자 • 블록정보 • 블록타임 • 블록헤더 • 비츠 • 세그윗 • 엉클블록 • 완결성 • 제네시스블록 • 타임스탬프 • 프룻 • 프룻체인 체인 더블체인 • 라이트닝 네트워크 • 라이트닝 루프 • 루트체인 • 루프체인 • 메인체인 • 방향성 비순환 그래프(DAG) • 베리파이어블 프루닝 • 블록격자 • 블록체인 • 사용자 활성화 소프트포크(UASF) • 사용자 활성화 하드포크(UAHF) • 사이드체인 • 서브체인 • 소프트포크 • 오페라체인 • 오프체인 • 온체인 • 인터체인 • 차일드체인 • 체인 • 탱글 • 테스트체인 • 토카막 네트워크 • 포크 • 포크체인 • 퓨어체인 • 프로덕트체인 • 프루닝 • 프리포크 • 플라즈마 알고리즘 • 플라즈마캐시 • 플래시 계층 • 하드포크 • 해시그래프 • 홀로체인 노드 검증인(밸리데이터) • 기본노드 • 노드 • 라이트노드 • 랜덤노드 • 마스터노드 • 베이킹노드 • 보조노드 • 보증노드 • 슈퍼노드(슈퍼대표, 대표노드) • 슬롯 • 슬롯리더 • 엔드포인트노드(레인저노드) • 의회 네트워크 • 작업노드 • 종단노드 • 종자노드(시드노드) • 중계노드 • 지갑노드 • 채굴노드(마이닝노드) • 쿼럼 • 풀노드 • 합의노드 샤딩 네트워크 샤딩 • 데이터베이스 샤딩 • 동적샤딩 • 샤드 • 샤딩 • 스테이트 샤딩 • 알고리즘 샤딩 • 적응형 상태 샤딩 • 체인샤딩 • 트랜잭션 샤딩 채굴 병합채굴 • 사전채굴 • 에이식(ASIC) • 에이식부스트 • 에이식 저항 • 일드파밍 • 채굴 • 채굴 난이도 • 채굴량 • 탄소감축채굴 • 페어런치 탈중앙화 TVL • 거버넌스 • 게임파이 • 다오(DAO) • 다이코(DAICO) • 닥(DAC) • 닥스(DAX) • 덱스(DEX) • 디앱(DApp) • 디지오(DGO) • 디튜브 • 디파이(DeFi) • 분산경제 • 분산원장(DLT) • 분산 클라우드 • 소셜파이 • 씨파이(C-Fi) • 오프체인 거버넌스 • 온체인 거버넌스 • 원장 • 준중앙화 • 중앙화 • 탈중앙화 • 탈중앙화 TPS • 탈중앙화 조직(DO) • 탈중앙화 지수(DQ) 분산아이디 DIDs • IETF • ToIP • 검증가능한 자격증명 • 검증인 • 디지털아이덴티티재단 • 발급자 • 보유자 • 분산아이디(DID) • 분산아이디 기관 • 분산아이디 인증(DID Auth) • 아이온 • 자기주권 • 자기주권신원 • 최소화된 자격증명 데이터 • 탈중앙화 키관리시스템 • 통합해석기 오라클 상호인증 블록체인 • 오라클 • 오라클 머신 • 오라클 문제 • 오라클 서비스 • 중간자 BIP BIP • BIP9 • BIP16 • BIP32 • BIP39 • BIP43 • BIP44 • BIP47 • BIP49 • BIP63 • BIP70 • BIP84 • BIP141 • BIP148 ERC ERC • ERC-20 • ERC-165 • ERC-223 • ERC-621 • ERC-721 • ERC-777 • ERC-827 • ERC-884 • ERC-998 • ERC-1155 • ERC-1404 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반