"차분기관"의 두 판 사이의 차이
(→작동원리) |
leejia1222 (토론 | 기여) |
||
| (다른 사용자 한 명의 중간 판 하나는 보이지 않습니다) | |||
| 5번째 줄: | 5번째 줄: | ||
==개요== | ==개요== | ||
| − | 1821년 영국, 천문학자이자 수학자인 [[찰스 배비지]]는 손으로 계산한 천문 테이블을 보고 오류를 발견했다. 그는 사람들의 오류를 보면서 계산 또한 증기를 사용하여 작동한다면 오류 발생 확률이 극히 낮아지며, 오류로 인해 발생하는 피해도 막을 수 있을 것이라 다짐했다. 이에 따라 찰스 배비지는 인쇄된 테이블의 오류의 위험을 제거하기에 기계로 만든 계산 엔진을 설계하고 구축하려고 시도 하게 되었다. 계산 엔진에 대한 그의 작업은 기계화된 산술방식에서 완전히 새로운 자동 계산 영역으로 전환되는 계기가 되었다. 또한, 그는 수학자였기 때문에 엔진의 기술 또한 수학 기술로 보았다.<ref name="출처">CHM, 〈[https://www.computerhistory.org/babbage/history/ THE BABBAGE ENGINE]〉, 《CHM》, </ref> 다음 해인 1822년 [[영국왕립학회]] 회장인 [[험프리 | + | 1821년 영국, 천문학자이자 수학자인 [[찰스 배비지]]는 손으로 계산한 천문 테이블을 보고 오류를 발견했다. 그는 사람들의 오류를 보면서 계산 또한 증기를 사용하여 작동한다면 오류 발생 확률이 극히 낮아지며, 오류로 인해 발생하는 피해도 막을 수 있을 것이라 다짐했다. 이에 따라 찰스 배비지는 인쇄된 테이블의 오류의 위험을 제거하기에 기계로 만든 계산 엔진을 설계하고 구축하려고 시도 하게 되었다. 계산 엔진에 대한 그의 작업은 기계화된 산술방식에서 완전히 새로운 자동 계산 영역으로 전환되는 계기가 되었다. 또한, 그는 수학자였기 때문에 엔진의 기술 또한 수학 기술로 보았다.<ref name="출처">CHM, 〈[https://www.computerhistory.org/babbage/history/ THE BABBAGE ENGINE]〉, 《CHM》, </ref> 다음 해인 1822년 [[영국왕립학회]] 회장인 [[험프리 데이비]](Humphry Davy) 경에게 탐색하는데 사용되는 로그 테이블의 자동생성 가능성에 대한 편지를 보내기 시작했다. 당시 사용 중인 천문학 테이블에 오류가 있었기 때문에 테이블 자동생산을 한다면 많은 이득을 볼 수 있었다. 이를 받아들인 영국 정부는 찰스 배비지에게 차분기관을 개발할 수 있도록 자금지원을 약속하였다. 찰스 배비지는 여러 기계공과 차분기관을 발명할 환경을 만들고 실험을 진행했다. 일반적으로 최대 30자리 숫자까지 결과를 산출하는 계산기를 생각했으며, [[톱니바퀴]]를 이용하여 0에서 9까지 표현하는 10진법 기법을 사용했다. 단순 계산 문제뿐만 아니라 여러 변수에 대한 복합적인 계산을 하는 로그함수, 삼차 함수에 대한 계산이 가능했다. 또한 데이터를 임시로 보관할 수 있는 저장공간이 있었으며, [[천공카드]]를 사용하여 해당 값의 출력이 가능했다.<ref>Paul A. Freiberger, 〈[https://www.britannica.com/technology/Difference-Engine Difference Engine]〉, 《britannica》</ref> |
| + | |||
| + | 차분기관은 계산 부분과 출력 간에 동일하게 사용되는 약 25,000개의 부품을 필요로했다. 만약 완성되었다면, 무게는 약 4톤이고 높이는 약 8피트로 예상한다. 그의 엔지니어인 조셉 클레멘트(Joseph Clement)와의 분쟁으로 인해 1832년 차분기관 작업이 중단되었고 정부 자금 또한 끊기게 되었다. 때문에 실제로 만들지는 못하고 찰스 배비지의 노트와 여러 논문만 존재하였다. 1991년 배비지의 탄생 200주년을 기념하여 영국의 런던 과학박물관에서 차분기관 및 [[해석기관]]을 제작하게 되어 오늘날 볼 수 있는 계산기 장치가 만들어졌다. 완성된 기계는 찰스 배비지가 의도 한 대로 작동했다. 8,000개의 부품이 계산 부분과 출력 장치 간에 균등하게 분할된다. 무게는 약 5톤이고 높이는 2미터, 길이는 3.5미터이며 가장 좁은 부분의 깊이는 18인치이다. 차분기관이 잘 작동한다는 의미는 그가 구현했던 수학적 메커니즘과 기계와의 결합이 오류가 없고 매우 정밀도가 높았음을 알 수 있다. 이러한 점에서 찰스 배비지는 독창성을 지닌 엔지니어로 여겨진다.<ref name="출처"></ref> | ||
==주요 인물== | ==주요 인물== | ||
===찰스 배비지=== | ===찰스 배비지=== | ||
| − | 찰스 배비지는 1791년 12월 26일 부유한 영국 은행가의 아들로 태어났다. 몸이 늘 허약하여서 어렸을 적부터 많은 고생을 하며 자라왔다. 1810년, [[케임브리지 대학교]]에 입학 하게 되고 그전까지 주로 가정교사에게 교육을 받았다. 찰스 배비지는 혼자 대수학을 깨우칠 정도로 수학에 관심이 많아 대학을 통해 더 깊이 공부하고자 하였다. 그의 실력을 인정받아 25세에 영국학사원 회원으로 선정되었으며, 1828년에는 아이작 뉴턴(Isaac Newton)과 스티븐 호킹(Stephen William Hawking)이 역임한 것으로 유명한 케임브리지 루카스 석좌교수직으로 뽑히기도 하였다. 이러함에도 불구하고 찰스 배비지는 해석기관의 설계도까지 내며 열정을 보였으나 실제로는 완성하지 못하였다. 사회적 지위, 정부 자금, 10년간의 설계 및 개발, 최고의 영국 엔지니어링 기술이 있음에도 소용없었다. 그 이유는 여전히 논쟁의 여지가 있지만, 실제 찰스 배비지는 매우 원칙적이며, 상대방을 쉽게 기분을 상하게 했고 그가 적으로 받아들인 사람들에 대해 맹렬한 대중 비판을 받아왔다. 해석기관의 부품을 하나하나 만들어야 해서 비용이 너무 많이 들고, 증기기관을 이용하기 때문에 압력과 톱니바퀴가 매우 정교해야 했으며, 영국 정부와의 자금협조, 지연, 신뢰성 실패 및 순수 과학과 응용과학 사이의 문화적 차이가 실패 요소로 이야기된다. 또한 찰스 배비지는 자신의 작업에 대해 강의하는 것을 싫어했고, 그의 엔진의 수학적 잠재력을 선포하거나 홍보하는 데 매우 게을렀다. 결과적으로 [[엔진]]은 오류 없는 [[테이블]]을 생성하기 위한 실질적인 유용성에 대해 평가를 받았으며 당시의 전문가들은 새로운 테이블이 실제로 필요하다는 데 동의하지 않았고 일부는 기존 테이블이 이미 충분히 정확하고 거대한 기계를 만드는 데 드는 큰 자본 비용에 대한 경제적 정당성이 없다고 주장했다. 결국, 그 시대에 주목받지 못한 기술이 되어버렸지만, 현재에 컴퓨터의 기초를 닦는 기술이 되었다.<ref>LG CNS, 〈[https://blog.lgcns.com/950 컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)']〉, | + | 찰스 배비지는 1791년 12월 26일 부유한 영국 은행가의 아들로 태어났다. 몸이 늘 허약하여서 어렸을 적부터 많은 고생을 하며 자라왔다. 1810년, [[케임브리지 대학교]]에 입학 하게 되고 그전까지 주로 가정교사에게 교육을 받았다. 찰스 배비지는 혼자 대수학을 깨우칠 정도로 수학에 관심이 많아 대학을 통해 더 깊이 공부하고자 하였다. 그의 실력을 인정받아 25세에 영국학사원 회원으로 선정되었으며, 1828년에는 아이작 뉴턴(Isaac Newton)과 스티븐 호킹(Stephen William Hawking)이 역임한 것으로 유명한 케임브리지 루카스 석좌교수직으로 뽑히기도 하였다. 이러함에도 불구하고 찰스 배비지는 해석기관의 설계도까지 내며 열정을 보였으나 실제로는 완성하지 못하였다. 사회적 지위, 정부 자금, 10년간의 설계 및 개발, 최고의 영국 엔지니어링 기술이 있음에도 소용없었다. 그 이유는 여전히 논쟁의 여지가 있지만, 실제 찰스 배비지는 매우 원칙적이며, 상대방을 쉽게 기분을 상하게 했고 그가 적으로 받아들인 사람들에 대해 맹렬한 대중 비판을 받아왔다. 해석기관의 부품을 하나하나 만들어야 해서 비용이 너무 많이 들고, 증기기관을 이용하기 때문에 압력과 톱니바퀴가 매우 정교해야 했으며, 영국 정부와의 자금협조, 지연, 신뢰성 실패 및 순수 과학과 응용과학 사이의 문화적 차이가 실패 요소로 이야기된다. 또한 찰스 배비지는 자신의 작업에 대해 강의하는 것을 싫어했고, 그의 엔진의 수학적 잠재력을 선포하거나 홍보하는 데 매우 게을렀다. 결과적으로 [[엔진]]은 오류 없는 [[테이블]]을 생성하기 위한 실질적인 유용성에 대해 평가를 받았으며 당시의 전문가들은 새로운 테이블이 실제로 필요하다는 데 동의하지 않았고 일부는 기존 테이블이 이미 충분히 정확하고 거대한 기계를 만드는 데 드는 큰 자본 비용에 대한 경제적 정당성이 없다고 주장했다. 결국, 그 시대에 주목받지 못한 기술이 되어버렸지만, 현재에 컴퓨터의 기초를 닦는 기술이 되었다.<ref>LG CNS, 〈[https://blog.lgcns.com/950 컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)']〉, 《엘지씨엔에스》, 2015-11-09</ref> |
==작동원리== | ==작동원리== | ||
| − | 차분기관은 피겨 휠(figure wheel) 기어를 기반으로 하며, 각각 0에서 9까지의 숫자를 나타낸다. 숫자 휠은 8개 열로 쌓여 있으며 각 열은 완전한 숫자를 나타내고, 각각의 열에 31개의 톱니바퀴가 | + | 차분기관은 피겨 휠(figure wheel) 기어를 기반으로 하며, 각각 0에서 9까지의 숫자를 나타낸다. 숫자 휠은 8개 열로 쌓여 있으며 각 열은 완전한 숫자를 나타내고, 각각의 열에 31개의 톱니바퀴가 있으며, 총 248개의 톱니바퀴가 모두 8개의 열에 고정되어 있다. 차분기관은 톱니바퀴축, 손으로 톱니를 돌려 값을 지정하는 핸드 크랭크, 중앙 톱니바퀴를 수평 막대로 움직임을 제공하는 캠, 수평막대의 앞뒤 이동과 엔진의 다른 부분에 대한 위아래의 움직임 또는 각도 이동을 하는 레버 및 랙, 핸드 크랭크로부터 엔진의 모든 길이를 베이스 근처에 있는 차축을 통해 움직임을 수신하는 고정관념 메커니즘, 전송 메커니즘의 결과를 받는 활 인쇄 및 스탬핑, 결과 전송 메커니즘으로 구성되어 있다. 또한 고정관념 메커니즘은 두 가지 주요 기술이 있는데 테이블을 이동하여 페이지 당 여러 열과 행을 조합하여 결과를 인쇄할 수 있고, 프린팅 휠과 프린팅 테이블 사이에 스탬핑이 수행되는 부드러운 소재를 담는 실제 팬이 존재한다. 핸드 크랭크에 몇 개의 피니언 기어를 통해 움직일 수 있고, 가운데에는 8개의 축이 숫자바퀴를 고정한다. 피겨 휠은 톱니가 40개인 기어이다. 차분기관은 대략 10년 정도밖에 없었지만, 피겨 휠은 훨씬 더 작았다. 바퀴 안에 다른 장치를 위한 공간을 만들기 위해 바퀴는 더 크지만 다른 것보다 더 작게 움직이는 특성이 있다. 휠은 축을 중심으로 자유롭게 회전을 한다. 모든 움직임은 바퀴를 통해 이루어지며, 바깥쪽과 안쪽에 있는 네 개의 바퀴를 통해 이루어진다. 외부에 새겨진 숫자는 출력이 인쇄 메커니즘에서 나오기 때문에 엔진을 설정하는 데 사용된다. 톱니바퀴의 숫자 6과 7 사이에있는 바깥쪽 펜촉은 9에서 0까지의 움직임을를 감지하는 데 사용되며. 펜촉이 두 숫자 사이에있을 것으로 예상되지만 실제로는 중요하지 않다. 새겨진 숫자가 메커니즘의 실제 0과 일치하지 않기 때문이다. |
| − | + | [[파일:숫자 추가..jpg|썸네일|200픽셀|숫자추가]] | |
| − | + | ===피겨 휠 원리=== | |
| + | 숫자를 추가하는 세부적인 과정은 다음과 같다. 자홍색의 섹터기어, 섹터 휠이 아래로 이동하고 양옆의 톱니와 맞물리게되어 함께 움직이게 된다. 두 개의 톱니는 서로 다른 숫자를 나타내기 때문에 서로 다른 시점에서 움직이게 된다. 복원 장치는 항상 톱니바퀴를 0으로 되돌린다. 이렇게 하면서, 톱니바퀴가 가지고 있는 숫자 값을 섹터 휠을 통해 뒷면에 표시된 수신 휠로 보내어 해당 값을 읽게된다. 만약에 복원 장치가 9를 들고 있을 경우 휠이 다시 내려오게 된다. 피겨 휠이 9에 위치하면 복원 장치가 서로 맞물려 섹터 휠로 옮기고 다음 숫자 휠이 나타나게 된다. 숫자가 적을수록 복원 장치와 피겨 휠의 내부의 톱니와 맞물리는데 시간이 걸리므로 섹터 휠로 전송할 데이터의 양이 적어지게 된다.<ref> satyam, 〈[http://satyam.com.ar/Babbage/en/index.html Babbage Difference Engine]〉, 《satyam》, </ref> | ||
==차분법== | ==차분법== | ||
| + | ===순차 메커니즘=== | ||
[[파일:기본 차분법.jpg|썸네일|400픽셀|순차 메커니즘 예시]] | [[파일:기본 차분법.jpg|썸네일|400픽셀|순차 메커니즘 예시]] | ||
| − | |||
| − | |||
| − | + | 찰스 배비지는 절대적이고 정확한 수학 표를 만들기 위해 차분기관을 사용하였다. 특히 천문학과 항해에는 사인, 코사인, 로그 등과 같은 표준 수학 함수 표가 필수적이였다. 당시 계산된 표는 계산 자체의 실수 나 조판 및 인쇄 과정에서 발생한 오류로 가득 많았기 때문에 항해 오류로 인해 많은 선박이 손실되었다. 이에 뉴턴의 분할차이 방법인 미적분을 사용하여 차분기관을 작동시켰다. 대부분의 계산에는 단순한 덧셈과 뺄셈이 포함되고, 표로 작성할 함수는 먼저 다항식에 의해 특정 범위에 대해 근사화된다. 다항식의 정도는 계산할 테이블의 원하는 정확도와 단일 다항식 근사치에 포함되는 함수 범위에 따라 달라진다. 이 방법은 프랑스의 수학자 [[가스파르 드 프로니]](Gaspard Francois de Prony)에 의해 처음 적용되었다. | |
| − | + | ||
| − | + | 1790년대 프랑스에서 14~29 자리까지 계산된 로그 및 삼각 함수 표 18권에 대한 원고를 제작했다. 소수의 전문 수학자들이 계산에 사용하기에 가장 적합한 공식을 결정한 다음, 두 번째 소규모 수학자 그룹이 공식을 사용하여 훨씬 더 큰 그룹의 초기값 세트를 계산했다. 세 번째 그룹은 동일한 계산을 독립적으로 수행하기 위해 두 세트로 나누어지고, 마지막으로 두 번째 그룹은 두 세트의 계산 결과를 비교하여 결과를 확인하기 위해 다시 사용되었다. 찰스 배비지는 세 번째 그룹의 전체 작업이 기계에 의해 제거될 수 있다는 것을 깨달았고, 또한 계산이 사람의 실수 없이 자동으로 이루어지므로 두 번째 그룹의 작업 대부분도 생략 할 수 있다는 사실을 알게 되었다. 우측 표는 2차 다항식에 관한 설명이다. 다음 테이블의 첫 번째 행만 주어지면 이제 함수 <math>x</math>의 임의 값에 대해 나머지 테이블을 더하기 만하면 된다. 차이 열의 다음 항목을 얻으려면 두 번째 차이 열의 동일한 행에서 차이 열의 현재 항목에 값을 추가하기만 하면 된다. 이와 같은 방법을 사용하여 테이블을 차례대로 구성할 수 있다. 단, 테이블 함수값을 구하기 전에 각각의 차이 값에 대한 부분의 표를 위로 올려주어 표준화 시켜야한다.<ref> Tim Robinson, 〈[http://www.meccano.us/difference_engines/index.html Difference Engines]〉, 《meccano》, 2007-05-28</ref> | |
| + | |||
| + | ===병렬 메커니즘=== | ||
| + | [[파일:병렬 메커니즘.jpg|썸네일|400픽셀|병렬 메커니즘]] | ||
| + | |||
| + | 찰스 배비지는 차분법을 이용하여 어떠한 다항식 값의 결과 테이블 한 행만 있어도 다음 변수 <math>x</math>에 대한 계산 값을 구할 수 있도록 병렬 메커니즘을 사용하였다. 만약 차분기관이 7자리 숫자까지 표현 한다면 병렬 메커니즘은 다음의 표와 같다. 유한방법을 사용하여 다항식의 값의 순서를 계산하고, 값의 차이를 구하기 전에 각 열의 첫 번째 값을 일치시켜준다. 유한 차분 방법의 속성은 행을 기억할 필요가 없다. 한 줄의 스토리지와 차별화된 엔진만 주어진다면 한 행을 가지고 계산을 구해낼 수 있다. 병렬 메커니즘에는 3가지 단계로 나뉜다. | ||
| + | |||
| + | 첫째, 차분법을 이용하여 <math>f(x)</math> 본래의 값과 이전값의 차이 값을 더해준다. 둘째, 그다음 해당 값의 결과가 나오면 오른쪽으로 한 칸 이동하여서 차이에 대한 값과 새로 나온 결과값을 더해 준다. 셋째, 첫 번째 방법과 동일하게 값을 더해주면 된다. 병렬 알고리즘을 구현하기 위해서는 수동으로 계산을 많이 해놓아야 구현하기가 쉽다. 기존의 순차 알고리즘의 방법보다 속도가 증가하게 된다. 자동화된 기계로 설비했고, 값을 하나하나 입력할 필요가 없기 때문이다. 그리고 톱니바퀴와 기어의 계산속도느 다항식의 차수와 무관하다. 병렬 알고리즘을 구현하기 위한 제어 메커니즘 및 하드웨어는 순차적인 알고리즘보다 설계와 구축이 더 간단한 장점이 있다. 병렬 메커니즘은 두 번째 차분기관부터 적용이 되었다. 옆의 표를 예시로 설명을 하면 8개의 레지스터를 가지는 7개의 가산기가 있다. 주어진 함수 <math>f(x)</math>에 따라 값이 달라진다. 순차 알고리즘과는 다르게 병렬 알고리즘에는 순서가 있다. 먼저 녹색계열의 수식부터 진행하게 된다. <math>R0+R1</math>, <math>R2+R3</math>, <math>R4+R5</math>, <math>R6+R7</math>을 진행한다. 그다음 나머지 값을 계산하고 다시 계산된 값을 가지고 순서대로 계산하면 병렬 알고리즘이 완성된다. 이같이 다항식의 값과 각각의 차이가 하나씩만 존재하여도 함수 <math>f(x)</math>에 관한 모든 값을 차분기관을 통하여 계산하고 결과를 얻을 수 있다.<ref> MechanicalComputing, 〈[https://www.youtube.com/watch?v=PFMBU17eo_4&list=TLPQMjQwODIwMjDLigvw9F7Imw&index=2 Babbage's Difference Engine No. 2, Part 1: The method of finite differences]〉, 《유튜브》, 2015-04-11</ref> | ||
| + | |||
{{각주}} | {{각주}} | ||
==참고자료== | ==참고자료== | ||
| − | * CHM, 〈[https://www.computerhistory.org/babbage/history/ THE BABBAGE ENGINE]〉, 《CHM》 | + | * CHM, 〈[https://www.computerhistory.org/babbage/history/ THE BABBAGE ENGINE]〉, 《CHM》 |
* Paul A. Freiberger, 〈[https://www.britannica.com/technology/Difference-Engine Difference Engine]〉, 《britannica》 | * Paul A. Freiberger, 〈[https://www.britannica.com/technology/Difference-Engine Difference Engine]〉, 《britannica》 | ||
| − | * satyam, 〈[http://satyam.com.ar/Babbage/en/index.html Babbage Difference Engine]〉, 《satyam》 | + | * satyam, 〈[http://satyam.com.ar/Babbage/en/index.html Babbage Difference Engine]〉, 《satyam》 |
* Tim Robinson, 〈[http://www.meccano.us/difference_engines/index.html Difference Engines]〉, 《meccano》, 2007-05-28 | * Tim Robinson, 〈[http://www.meccano.us/difference_engines/index.html Difference Engines]〉, 《meccano》, 2007-05-28 | ||
| − | * MechanicalComputing, 〈[https://www.youtube.com/watch?v=PFMBU17eo_4&list=TLPQMjQwODIwMjDLigvw9F7Imw&index=2 Babbage's Difference Engine No. 2, Part 1: The method of finite differences]〉, 《유튜브》, 2015-04-11 | + | * MechanicalComputing, 〈[https://www.youtube.com/watch?v=PFMBU17eo_4&list=TLPQMjQwODIwMjDLigvw9F7Imw&index=2 Babbage's Difference Engine No. 2, Part 1: The method of finite differences]〉, 《유튜브》, 2015-04-11 |
| − | * LG CNS, 〈[https://blog.lgcns.com/950 컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)']〉, | + | * LG CNS, 〈[https://blog.lgcns.com/950 컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)']〉, 《엘지씨엔에스》, 2015-11-09 |
==같이 보기== | ==같이 보기== | ||
2020년 8월 31일 (월) 16:01 기준 최신판

차분기관(Difference Engine)이란 기계공학자 찰스 배비지(Charles babbage) 만든 다항식 계산기이다. 흔히 미분기로도 불린다.
개요[편집]
1821년 영국, 천문학자이자 수학자인 찰스 배비지는 손으로 계산한 천문 테이블을 보고 오류를 발견했다. 그는 사람들의 오류를 보면서 계산 또한 증기를 사용하여 작동한다면 오류 발생 확률이 극히 낮아지며, 오류로 인해 발생하는 피해도 막을 수 있을 것이라 다짐했다. 이에 따라 찰스 배비지는 인쇄된 테이블의 오류의 위험을 제거하기에 기계로 만든 계산 엔진을 설계하고 구축하려고 시도 하게 되었다. 계산 엔진에 대한 그의 작업은 기계화된 산술방식에서 완전히 새로운 자동 계산 영역으로 전환되는 계기가 되었다. 또한, 그는 수학자였기 때문에 엔진의 기술 또한 수학 기술로 보았다.[1] 다음 해인 1822년 영국왕립학회 회장인 험프리 데이비(Humphry Davy) 경에게 탐색하는데 사용되는 로그 테이블의 자동생성 가능성에 대한 편지를 보내기 시작했다. 당시 사용 중인 천문학 테이블에 오류가 있었기 때문에 테이블 자동생산을 한다면 많은 이득을 볼 수 있었다. 이를 받아들인 영국 정부는 찰스 배비지에게 차분기관을 개발할 수 있도록 자금지원을 약속하였다. 찰스 배비지는 여러 기계공과 차분기관을 발명할 환경을 만들고 실험을 진행했다. 일반적으로 최대 30자리 숫자까지 결과를 산출하는 계산기를 생각했으며, 톱니바퀴를 이용하여 0에서 9까지 표현하는 10진법 기법을 사용했다. 단순 계산 문제뿐만 아니라 여러 변수에 대한 복합적인 계산을 하는 로그함수, 삼차 함수에 대한 계산이 가능했다. 또한 데이터를 임시로 보관할 수 있는 저장공간이 있었으며, 천공카드를 사용하여 해당 값의 출력이 가능했다.[2]
차분기관은 계산 부분과 출력 간에 동일하게 사용되는 약 25,000개의 부품을 필요로했다. 만약 완성되었다면, 무게는 약 4톤이고 높이는 약 8피트로 예상한다. 그의 엔지니어인 조셉 클레멘트(Joseph Clement)와의 분쟁으로 인해 1832년 차분기관 작업이 중단되었고 정부 자금 또한 끊기게 되었다. 때문에 실제로 만들지는 못하고 찰스 배비지의 노트와 여러 논문만 존재하였다. 1991년 배비지의 탄생 200주년을 기념하여 영국의 런던 과학박물관에서 차분기관 및 해석기관을 제작하게 되어 오늘날 볼 수 있는 계산기 장치가 만들어졌다. 완성된 기계는 찰스 배비지가 의도 한 대로 작동했다. 8,000개의 부품이 계산 부분과 출력 장치 간에 균등하게 분할된다. 무게는 약 5톤이고 높이는 2미터, 길이는 3.5미터이며 가장 좁은 부분의 깊이는 18인치이다. 차분기관이 잘 작동한다는 의미는 그가 구현했던 수학적 메커니즘과 기계와의 결합이 오류가 없고 매우 정밀도가 높았음을 알 수 있다. 이러한 점에서 찰스 배비지는 독창성을 지닌 엔지니어로 여겨진다.[1]
주요 인물[편집]
찰스 배비지[편집]
찰스 배비지는 1791년 12월 26일 부유한 영국 은행가의 아들로 태어났다. 몸이 늘 허약하여서 어렸을 적부터 많은 고생을 하며 자라왔다. 1810년, 케임브리지 대학교에 입학 하게 되고 그전까지 주로 가정교사에게 교육을 받았다. 찰스 배비지는 혼자 대수학을 깨우칠 정도로 수학에 관심이 많아 대학을 통해 더 깊이 공부하고자 하였다. 그의 실력을 인정받아 25세에 영국학사원 회원으로 선정되었으며, 1828년에는 아이작 뉴턴(Isaac Newton)과 스티븐 호킹(Stephen William Hawking)이 역임한 것으로 유명한 케임브리지 루카스 석좌교수직으로 뽑히기도 하였다. 이러함에도 불구하고 찰스 배비지는 해석기관의 설계도까지 내며 열정을 보였으나 실제로는 완성하지 못하였다. 사회적 지위, 정부 자금, 10년간의 설계 및 개발, 최고의 영국 엔지니어링 기술이 있음에도 소용없었다. 그 이유는 여전히 논쟁의 여지가 있지만, 실제 찰스 배비지는 매우 원칙적이며, 상대방을 쉽게 기분을 상하게 했고 그가 적으로 받아들인 사람들에 대해 맹렬한 대중 비판을 받아왔다. 해석기관의 부품을 하나하나 만들어야 해서 비용이 너무 많이 들고, 증기기관을 이용하기 때문에 압력과 톱니바퀴가 매우 정교해야 했으며, 영국 정부와의 자금협조, 지연, 신뢰성 실패 및 순수 과학과 응용과학 사이의 문화적 차이가 실패 요소로 이야기된다. 또한 찰스 배비지는 자신의 작업에 대해 강의하는 것을 싫어했고, 그의 엔진의 수학적 잠재력을 선포하거나 홍보하는 데 매우 게을렀다. 결과적으로 엔진은 오류 없는 테이블을 생성하기 위한 실질적인 유용성에 대해 평가를 받았으며 당시의 전문가들은 새로운 테이블이 실제로 필요하다는 데 동의하지 않았고 일부는 기존 테이블이 이미 충분히 정확하고 거대한 기계를 만드는 데 드는 큰 자본 비용에 대한 경제적 정당성이 없다고 주장했다. 결국, 그 시대에 주목받지 못한 기술이 되어버렸지만, 현재에 컴퓨터의 기초를 닦는 기술이 되었다.[3]
작동원리[편집]
차분기관은 피겨 휠(figure wheel) 기어를 기반으로 하며, 각각 0에서 9까지의 숫자를 나타낸다. 숫자 휠은 8개 열로 쌓여 있으며 각 열은 완전한 숫자를 나타내고, 각각의 열에 31개의 톱니바퀴가 있으며, 총 248개의 톱니바퀴가 모두 8개의 열에 고정되어 있다. 차분기관은 톱니바퀴축, 손으로 톱니를 돌려 값을 지정하는 핸드 크랭크, 중앙 톱니바퀴를 수평 막대로 움직임을 제공하는 캠, 수평막대의 앞뒤 이동과 엔진의 다른 부분에 대한 위아래의 움직임 또는 각도 이동을 하는 레버 및 랙, 핸드 크랭크로부터 엔진의 모든 길이를 베이스 근처에 있는 차축을 통해 움직임을 수신하는 고정관념 메커니즘, 전송 메커니즘의 결과를 받는 활 인쇄 및 스탬핑, 결과 전송 메커니즘으로 구성되어 있다. 또한 고정관념 메커니즘은 두 가지 주요 기술이 있는데 테이블을 이동하여 페이지 당 여러 열과 행을 조합하여 결과를 인쇄할 수 있고, 프린팅 휠과 프린팅 테이블 사이에 스탬핑이 수행되는 부드러운 소재를 담는 실제 팬이 존재한다. 핸드 크랭크에 몇 개의 피니언 기어를 통해 움직일 수 있고, 가운데에는 8개의 축이 숫자바퀴를 고정한다. 피겨 휠은 톱니가 40개인 기어이다. 차분기관은 대략 10년 정도밖에 없었지만, 피겨 휠은 훨씬 더 작았다. 바퀴 안에 다른 장치를 위한 공간을 만들기 위해 바퀴는 더 크지만 다른 것보다 더 작게 움직이는 특성이 있다. 휠은 축을 중심으로 자유롭게 회전을 한다. 모든 움직임은 바퀴를 통해 이루어지며, 바깥쪽과 안쪽에 있는 네 개의 바퀴를 통해 이루어진다. 외부에 새겨진 숫자는 출력이 인쇄 메커니즘에서 나오기 때문에 엔진을 설정하는 데 사용된다. 톱니바퀴의 숫자 6과 7 사이에있는 바깥쪽 펜촉은 9에서 0까지의 움직임을를 감지하는 데 사용되며. 펜촉이 두 숫자 사이에있을 것으로 예상되지만 실제로는 중요하지 않다. 새겨진 숫자가 메커니즘의 실제 0과 일치하지 않기 때문이다.
피겨 휠 원리[편집]
숫자를 추가하는 세부적인 과정은 다음과 같다. 자홍색의 섹터기어, 섹터 휠이 아래로 이동하고 양옆의 톱니와 맞물리게되어 함께 움직이게 된다. 두 개의 톱니는 서로 다른 숫자를 나타내기 때문에 서로 다른 시점에서 움직이게 된다. 복원 장치는 항상 톱니바퀴를 0으로 되돌린다. 이렇게 하면서, 톱니바퀴가 가지고 있는 숫자 값을 섹터 휠을 통해 뒷면에 표시된 수신 휠로 보내어 해당 값을 읽게된다. 만약에 복원 장치가 9를 들고 있을 경우 휠이 다시 내려오게 된다. 피겨 휠이 9에 위치하면 복원 장치가 서로 맞물려 섹터 휠로 옮기고 다음 숫자 휠이 나타나게 된다. 숫자가 적을수록 복원 장치와 피겨 휠의 내부의 톱니와 맞물리는데 시간이 걸리므로 섹터 휠로 전송할 데이터의 양이 적어지게 된다.[4]
차분법[편집]
순차 메커니즘[편집]
찰스 배비지는 절대적이고 정확한 수학 표를 만들기 위해 차분기관을 사용하였다. 특히 천문학과 항해에는 사인, 코사인, 로그 등과 같은 표준 수학 함수 표가 필수적이였다. 당시 계산된 표는 계산 자체의 실수 나 조판 및 인쇄 과정에서 발생한 오류로 가득 많았기 때문에 항해 오류로 인해 많은 선박이 손실되었다. 이에 뉴턴의 분할차이 방법인 미적분을 사용하여 차분기관을 작동시켰다. 대부분의 계산에는 단순한 덧셈과 뺄셈이 포함되고, 표로 작성할 함수는 먼저 다항식에 의해 특정 범위에 대해 근사화된다. 다항식의 정도는 계산할 테이블의 원하는 정확도와 단일 다항식 근사치에 포함되는 함수 범위에 따라 달라진다. 이 방법은 프랑스의 수학자 가스파르 드 프로니(Gaspard Francois de Prony)에 의해 처음 적용되었다.
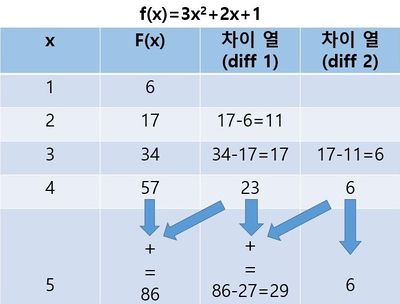
1790년대 프랑스에서 14~29 자리까지 계산된 로그 및 삼각 함수 표 18권에 대한 원고를 제작했다. 소수의 전문 수학자들이 계산에 사용하기에 가장 적합한 공식을 결정한 다음, 두 번째 소규모 수학자 그룹이 공식을 사용하여 훨씬 더 큰 그룹의 초기값 세트를 계산했다. 세 번째 그룹은 동일한 계산을 독립적으로 수행하기 위해 두 세트로 나누어지고, 마지막으로 두 번째 그룹은 두 세트의 계산 결과를 비교하여 결과를 확인하기 위해 다시 사용되었다. 찰스 배비지는 세 번째 그룹의 전체 작업이 기계에 의해 제거될 수 있다는 것을 깨달았고, 또한 계산이 사람의 실수 없이 자동으로 이루어지므로 두 번째 그룹의 작업 대부분도 생략 할 수 있다는 사실을 알게 되었다. 우측 표는 2차 다항식에 관한 설명이다. 다음 테이블의 첫 번째 행만 주어지면 이제 함수 의 임의 값에 대해 나머지 테이블을 더하기 만하면 된다. 차이 열의 다음 항목을 얻으려면 두 번째 차이 열의 동일한 행에서 차이 열의 현재 항목에 값을 추가하기만 하면 된다. 이와 같은 방법을 사용하여 테이블을 차례대로 구성할 수 있다. 단, 테이블 함수값을 구하기 전에 각각의 차이 값에 대한 부분의 표를 위로 올려주어 표준화 시켜야한다.[5]
병렬 메커니즘[편집]
찰스 배비지는 차분법을 이용하여 어떠한 다항식 값의 결과 테이블 한 행만 있어도 다음 변수 에 대한 계산 값을 구할 수 있도록 병렬 메커니즘을 사용하였다. 만약 차분기관이 7자리 숫자까지 표현 한다면 병렬 메커니즘은 다음의 표와 같다. 유한방법을 사용하여 다항식의 값의 순서를 계산하고, 값의 차이를 구하기 전에 각 열의 첫 번째 값을 일치시켜준다. 유한 차분 방법의 속성은 행을 기억할 필요가 없다. 한 줄의 스토리지와 차별화된 엔진만 주어진다면 한 행을 가지고 계산을 구해낼 수 있다. 병렬 메커니즘에는 3가지 단계로 나뉜다.
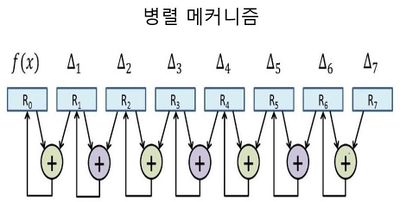
첫째, 차분법을 이용하여 본래의 값과 이전값의 차이 값을 더해준다. 둘째, 그다음 해당 값의 결과가 나오면 오른쪽으로 한 칸 이동하여서 차이에 대한 값과 새로 나온 결과값을 더해 준다. 셋째, 첫 번째 방법과 동일하게 값을 더해주면 된다. 병렬 알고리즘을 구현하기 위해서는 수동으로 계산을 많이 해놓아야 구현하기가 쉽다. 기존의 순차 알고리즘의 방법보다 속도가 증가하게 된다. 자동화된 기계로 설비했고, 값을 하나하나 입력할 필요가 없기 때문이다. 그리고 톱니바퀴와 기어의 계산속도느 다항식의 차수와 무관하다. 병렬 알고리즘을 구현하기 위한 제어 메커니즘 및 하드웨어는 순차적인 알고리즘보다 설계와 구축이 더 간단한 장점이 있다. 병렬 메커니즘은 두 번째 차분기관부터 적용이 되었다. 옆의 표를 예시로 설명을 하면 8개의 레지스터를 가지는 7개의 가산기가 있다. 주어진 함수 에 따라 값이 달라진다. 순차 알고리즘과는 다르게 병렬 알고리즘에는 순서가 있다. 먼저 녹색계열의 수식부터 진행하게 된다. , , , 을 진행한다. 그다음 나머지 값을 계산하고 다시 계산된 값을 가지고 순서대로 계산하면 병렬 알고리즘이 완성된다. 이같이 다항식의 값과 각각의 차이가 하나씩만 존재하여도 함수 에 관한 모든 값을 차분기관을 통하여 계산하고 결과를 얻을 수 있다.[6]
각주[편집]
- ↑ 1.0 1.1 CHM, 〈THE BABBAGE ENGINE〉, 《CHM》,
- ↑ Paul A. Freiberger, 〈Difference Engine〉, 《britannica》
- ↑ LG CNS, 〈컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)'〉, 《엘지씨엔에스》, 2015-11-09
- ↑ satyam, 〈Babbage Difference Engine〉, 《satyam》,
- ↑ Tim Robinson, 〈Difference Engines〉, 《meccano》, 2007-05-28
- ↑ MechanicalComputing, 〈Babbage's Difference Engine No. 2, Part 1: The method of finite differences〉, 《유튜브》, 2015-04-11
참고자료[편집]
- CHM, 〈THE BABBAGE ENGINE〉, 《CHM》
- Paul A. Freiberger, 〈Difference Engine〉, 《britannica》
- satyam, 〈Babbage Difference Engine〉, 《satyam》
- Tim Robinson, 〈Difference Engines〉, 《meccano》, 2007-05-28
- MechanicalComputing, 〈Babbage's Difference Engine No. 2, Part 1: The method of finite differences〉, 《유튜브》, 2015-04-11
- LG CNS, 〈컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)'〉, 《엘지씨엔에스》, 2015-11-09
같이 보기[편집]

 위키원
위키원