해석기관
해석기관이란 영국의 수학자이자 기계공학자인 찰스 배비지(Charles Babbage)가 만든 프로그램이 가능한 최초의 기계식 컴퓨터이다. 입력, 출력, 제어, 저장처리가 모두 가능하였고 오늘날의 컴퓨터의 기본구조에 있어 많은 표본이 되었다.
개요
찰스 배비지는 영국 정부의 지원을 받아 가며 본래 차분기관(Difference engine) 즉 미분 기계를 만들어내고 있었다. 하지만 찰스 배비지의 너무나도 완벽하고 꼼꼼한 성향으로 인해 본인을 도와주는 조수와의 다툼과 부품개발이 오랜시 간이 소요되고 자금의 사용량이 너무 많아졌다. 그리고 영국 정부는 컴퓨터에 대한 수요가 많지 않은 상태에서 자금지원을 한다는 것은 무리가 있었기 때문에 찰스 배비지에게 자금지원을 끊게 되었고, 이로 인해 뺄셈을 이용한 차분기관의 발명은 끝나게 되었다. 하지만 찰스 배비지 기계발명에 대한 생각을 머릿속으로 끊임없이 했고 1837년 처음으로 해석기관을 발표하였고 1843년 천공카드 를 이용하여 증기로 움직이는 해석기관을 만들었다. 톱니바퀴와 기어의 수가 너무 많기 때문에 무거워 사람의 힘으로는 기계를 작동할 수 없었다. 해석기관은 차분기관이 할 수 있는 모든 일을 수행하고 근사 다항식, 로그, 삼차 함수, 천문학 실험 도표의 계산까지 가능하였다. 해석기관은 오늘날의 컴퓨터 프로그래밍처럼 입력으로 주어진 명령어를 실행(프로세스)할 수 있었으며, 주어진 명령어들을 고쳐 기계의 기능까지도 바꿀 수 있었다. 또한 천공카드를 이용하여 데이터를 불러오고 반복과 배열문을 계산하기도 했다. 그러므로 해석기관을 오늘날 컴퓨터의 시초, 아버지라고도 부른다. 해석기관은 원판으로 이루어진 여러 기둥이 있고 원판 둘레에는 숫자가 적혀있다. 이 기둥들은 찰스 배비지가 '저장소'라고도 불렀으며 일종의 메모리 역활이었다. 저장소 기둥에 나타난 숫자들은 처리 과정을 거치며 다른 기둥으로 옮겨질 수 있었다. 기둥은 저장소에 있는 데이터에 제작소가 쉽게 접근해 데이터를 처리하고 다시 저장소에 쓸 수 있도록 배치돼 있었다. 찰스 배비지는 1871년 사망 전까지 해석기관을 실현하기 위해 연구에 몰두했다. 하지만 찰스 배비지가 생각한 이 기술은 당시에 실현되기에 기술 역량의 정확도 수준을 뛰어넘은지라 실제 완성품이 나오는 것은 불가능하였고 결국 설계도만 남게 되었다. 오늘날에는 1990년대 영국 런던의 과학 박물관에서 찰스 배비지가 남긴 여러 서적과 자료를 가지고 해석기관의 모형을 만들었으며 아무런 오차 없이 계산을 하는 것을 보며 찰스 배비지의 아이디어가 현실이 되었고 오류가 없음을 주장하게 되었다. 약 4,000개의 부품이 필요했고 그 무게는 3톤정도 였다. 찰스 배비지의 시대를 앞서간 생각은 약 100여 년이 지나서야 나타나게 되었다.[1]
작동원리
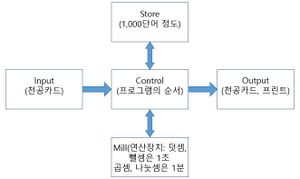
해석기관은 차분기관과 달리 다양한 데이터 처리가 가능하다. 10진법을 사용했으며 증기기관을 통해 핸들을 돌려 작동하도록 설계되었다. 약 30미터의 길이에 10미터 넓이 정도의 크기이며 자카르 방직기 기술을 이용한 천공카드를 사용하여 이진수로 데이터를 기록하고 제작소의 동작을 바꿀 수 있었다. 해석기관에는 50자리의 숫자 1,000개를 저장할 수 있는 저장소(Store)가 있고, 산술 논리 장치에는 사칙 연산과 비교 연산, 그리고 제곱근 계산 기능까지 제공하였다. 제작소 내부에서는 각각의 개별 연산에 해당하는 마이크로프로그램이 제작소를 통제한다. 마이크로프로그램은 배럴이라고 부른다. 자료는 저장소에서 제조소로 전송해서 처리하고, 저장소로 다시 돌려보내어 나중에 재사용할 수 있도록 했다. 찰스 배비지의 설계도엔 각기 40자리의 숫자를 저장할 수 있는 100개의 저장 장치(대략 1.7KB)가 자리하고 있다. 더 나아가서 1,000개의 저장장치(17KB)와 외부 저장장치 곧 오늘날의 디스크 구실을 하는 천공카드를 갖춘 기관이 필요할 거라고 예상했다.[2] 천공카드를 사용하여 원하는 해당 값을 출력(print)할 수 있었다. 스토어는 엔진의 밀(Mill)과 분리되어 있는데, 밀은 전자 컴퓨터의 중앙 처리 유닛과 비슷한 연산 처리를 수행한다. 밀은 최신 프로세서와 마찬가지로 가장 즉시 작동되는 번호 레지스터를 저장하기 위해 제공되었다. 외부에서 제공되는 사용자 지향 명령을 내부 하드웨어의 세부 제어로 변환하기 위한 제어 메커니즘 및 동기화 메커니즘은 신중하게 시간을 정한 순서대로 세부 단계를 수행하였다. 산술 작업을 수행하는 데 필요한 일련의 소규모 작업은 배럴이라고 하는 거대한 드럼에 의해 제어되었다. 배럴에는 오르골 드럼이나 배럴 오르간의 핀과 거의 같은 방식으로 외부 표면에 스터드가 고정되어 있다. 배럴은 엔진의 내부 동작을 조정하고 곱셈, 나눗셈, 더하기, 빼기 및 기타 산술 연산이 수행되는 방법을 자세히 지정한다. 실제 기계에서 배럴은 수천 개의 부품의 상호 작용을 제어하고 조정했기 때문에 크기가 매우 크고, 각 열에는 최대 200개의 스터드 위치가 포함되며 각 배럴에는 50-100개의 개별 열이 존재했다. 배럴은 서로 밀접하게 조정 되어야하고 배럴이 회전함에 따라 스터드가 메커니즘의 특정 동작을 활성화하고 스터드의 위치와 배열이 각 동작의 동작과 상대적 타이밍을 결정했다. 따라서 드럼을 돌리는 동작은 원하는 높은 수준의 작업을 수행하기 위해 일련의 동작을 자동으로 실행한다. 이 프로세스는 엔진 내부에 있으며 논리적으로 사용자에게는 보이지 않게 된다. 이 기술은 컴퓨팅에서 현재는 따라서 드럼을 돌리는 동작은 원하는 높은 수준의 작업을 수행하기 위해 일련의 동작을 자동으로 실행한다. 이 프로세스는 엔진 내부에 있으며 논리적으로 사용자에게는 보이지 않는다. 해석기관은 분기(branching), 루핑(looping) 그리고 병렬처리와 같이 오늘날 컴퓨터에서 볼 수 있는 기능들을 사용하고 있었다. 옆의 그림에서도 보면 천공카드에 있는 데이터를 사용하여 그 값을 톱니바퀴와 기어를 통해 처리(계산)하고 해당 결과가 천공카드 또는 프린트에 나오게 된다. [3]
해석기관을 사용하여 연립방정식에서 미지수 x의 값을 구할 수 있다. mx=ny=d m'x+n'y=d' 두 식을 각각 n과 n'로 나누고 식을 정리 하면 다음과 같다. x=(dn'-d'n)(n'm-nm') 해석기관은 m,n,d,m'n',d'의 값만 주어지면 x값을 구할 수 있으며 그 값들이 데이터 기둥에 저장되면 데이터 처리가 가능하다.
- 천공카드
- 18세기 여러 섬유업자들은 태엽이 달린 기계장치를 모방하여 일정한 움직임을 반복적으로 수행하는 자동기계를 고안하고 있었다. 그중 1801년 조셉 마리 자카르는 종아 카드에 구멍을 뚫어 정보를 표현하고 이를 기반으로 작물이 자동 생산할 수 있는 자카르 직기 곧 천공카드를 개발했다. 천공 종이를 사용했던 이전 기계들과는 달리 천공카드를 사용했다. 천공카드는 구멍이 있는지에 여부에 따라 데이터를 읽는 값이 달라진다. 그리고 일정한 패턴도 존재하여 반복하여 기계를 작동시킬 수도 있다. 이를 통하여 오늘날의 컴퓨터 프로그래밍의 원리가 되었다. 찰스 배비지는 이에 영감을 받아 천공카드를 이용하여 해석기관을 제작하게 되었다. 천공카드를 통해 해석기관을 프로그램할 수 있으며 20여 자리 숫자까지 정확한 연산을 자동으로 수행할 수 있었다.[4] 학교시험때 한 번쯤 사용해본 OMR카드가 천공카드의 원리를 사용한다. 원하는 곳에 마킹을 하고 기계에 넣으면 해당 값을 읽는 것처럼 천공카드는 대신 각각의 구멍을 뚫어 일정한 값을 부여하고 기계에 해당 값을 입력하게 되어 사용할 수 있다. 오늘날에는 흔히 Hollerith 카드 또는 펀치카드(punched card)라고 부른다. 컴퓨터가 처음 등장하였을 때 프로그래머는 손으로 프로그램을 작성한 다음 천공 카드 기계를 사용하여 프로그램 코드를 일련의 천공 카드로 변환하는 과정을 거쳐야만 했다. 프로그래머는 카드 더미를 컴퓨터로 가져가 카드 리더기에 카드를 넣어 프로그램을 입력한다. 천공 카드 기계를 사용하면 한 문자를 나타내는 각 열에 구멍을 뚫어 데이터를 카드에 입력 할 수 있다. 카드가 완성되거나 돌아가기 키를 누르면 카드는 해당 정보를 기술적으로 저장한다. 각 카드에는 많은 양의 데이터가 저장되기 때문에 천공 카드를 사용하여 프로그램을 작성하면 코드 한 줄당, 카드 한 개씩 천공 카드 스택을 필요로한다. 프로그램을 로드하거나 천공 카드 데이터를 읽기 위해 각 카드를 천공 카드 리더기에 삽입하여 카드에서 컴퓨터로 데이터를 입력한다. 카드가 삽입되면 펀치 카드 판독기가 카드의 왼쪽 상단에서 시작하여 위에서 아래로 수직으로 읽게 되고 카드 리더기가 열을 읽은 후 다음 열로 이동한다. 대부분의 최신 천공 카드는 각 카드에 포함 된 내용을 카드 상단에 인쇄했다. 따라서 이러한 카드의 경우 카드 상단을 검사하여 카드에 무엇이 저장되었는지 확인할 수 있다. 카드에서 오류가 발견되면 다시 인쇄되고 카드 상단에 데이터가 인쇄되지 않은 경우 사람은 표시되는 숫자를 알고 각 열을 수동으로 번역해야 한다. 현대 컴퓨터에 익숙하다면 바이너리 01101000과01101001 이 104 와 105 와 같다. 초기 컴퓨터는 오늘날의 컴퓨터와 같은 파일을 저장할 수 없었기에, 데이터 파일이나 프로그램을 만들거나 다른 컴퓨터에서 해당 데이터를 사용하는 유일한 방법은 천공 카드를 사용하는 것이었다. 하지만 오늘날에는 마그네틱 미디어가 만들어지고 저렴해지기 시작한 후 천공 카드 사용이 중단되었다. 해석기관에 천공카드가 사용될 때에는 원하는 방정식이나 계산을 해석기관에 직접 입력하고 천공카드를 넣어 데이터 입력값을 정한다. 그 후 계산이 되면 천공카드에 원하는 방식이 입력되어 사용이 가능하다.[5]
- 프로그램 메커니즘
- 찰스 배비지는 해석기관은 100% 완성하지 못한 채 세상을 떠났다. 오늘날 수많은 논문과 그의 설계도를 가지고 해석기관을 재현했다. 해석기관의 프로그램은 제어와 흐름, 및 단순 루프와 중첩 루프의 공식화를 다룬다. 인터넷상에 여러 자료와 설계도가 있지만 실제로는 몇천 장의 분량이고 런던 박물관 외에는 전부 요약된 설계도이기 때문에 직접 만드는 것은 매우 어려워 보인다. 찰스 배비지의 해석기관은 배럴 마이크로 프로그래밍으로 나눗셈을 하고 기본적인 분기와 반복 아이디어의 명령을 보여주고 덧셈과 뺄셈의 마이크로 프로그래밍에 대한 완벽한 기술을 보여준다. 찰스 배비지가 사용자 수준 프로그래밍 아이디어를 탐구 한것을 알 수있다. 데이터 구조화 문제는 마이크로 프로그래밍 수준에서 발생하지 않았다. 찰스 배비지의 아이디어가 사용자 수준 프로그램에서 반복 계수를 위한 제어 메커니즘에 사용이 된다. 분석 엔진이 작동 상태로 전환 되었으면 하드웨어 관점에서 볼 때 분석 엔진에서 수행할 계산을 지정하려면 두 줄의 천공 카드가 필요했다. 하나의 문자열인 연산 카드는 수행할 산술 연산을 지정했고, 두 번째 문자열인 "변수 카드"는 피연산자를 포함하고 결과를 수신할 저장소의 축을 지정한다. 이 두 문자열은 전자 디지털 컴퓨터에서 명령어의 연산 및 피연산자 필드와 같이 단일 명령어의 개별 부분으로 간주할 수 없다. 연산 및 가변 카드는 다음의 지시에 따라 서로 독립적으로 이동하고 반복하도록 의도되었기 때문이다. 이는 저장소에 입력할 숫자 값을 지정하거나 외부 저장을 위해 저장소에서 다시 숫자를 수신하는 데 사용되다. 가변 카드는 공장에 공급되는 데이터의 소스 또는 공장에서 반환된 데이터의 수신자가 될 저장소의 축을 지정한다. 현대 용어로는 사용할 변수의 메모리 주소를 지정하는 의미이다. 찰스 배비지는 연산용 기호와 수학적 표기법의 기호를 구별할 필요가 있다는 생각에서 비롯된 철학적 근거로 연산 및 가변 카드를 분리하도록 유도하였다. 이러한 견해는 그가 연립 방정식의 해와 같은 계산에 필요한 카드를 고려했을 때 매우 유용했을 것이다. 그는 또한 새로운 데이터 세트에서 검증 된 프로그램을 다시 실행하고 여러 엔진에서 프로그램을 공유하는 것이 중요하다는 것도 알고 있었다. 따라서 데이터를 작업과 독립적으로 지정하는 것은 자연스럽고 실용적인 접근 방식이다. 행 축소를 수행하는 데 필요한 작업 패턴은 매우 간단하며 작업 카드의 간단한 루프를 쉽게 찾을 수 있다. 저장소에서 단일 축만 지정할 수 있는 가변 카드에는 이러한 간단한 루프 구조가 없다. 그 당시에는 저장소에 가변 주소라는 개념이 없었기 때문에 해석기관은 상점에서 피연산자의 위치를 계산할 수 없었다. 찰스 배비지가 실제 컴퓨터를 프로그래밍한 경험이 없다는 점을 염두에 둔다면 프로그래밍 기술이 굉장히 뛰어난 것을 알 수 있다. 조합 카드는 변수 카드에서 제공하는 참조 별 호출 값으로 서브 루틴을 호출하는 제어 흐름 프로그래밍 용어를 제공했다. 그의 프로그래밍 개념에는 루프, 서브 루틴 및 브랜치 등이 포함되어 있다. 그러나 그는 실제 컴퓨터 프로그래밍 경험이 없었기 때문에 고급 언어, 통역사 또는 컴파일러의 현대 개념에는 도달하지 못했다.[3]
설계도
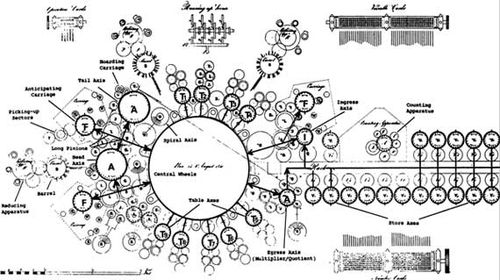
해석기관의 설계도는 옆의 그림과 같다. 오른쪽에는 11개의 가변 축을 포함하는 저장소구역으로 나누어진다. 실제 구현한 해석기관은 더 많은 가변 축을 가졌을것이라 예상한다. 찰스 배배지의 개인 노트를 보면 100개 이상, 많게든 1000개이상 필요하다고 기록되어있다. 각 가변 축에는 중앙 축을 중심으로 회전하는 많은 숫자 바퀴가 포함되어 있으며, 각각은 해당 변수의 한 자리를 보유하고 있다. 일반적으로 변수 당 40자리 숫자로 되어있으며 양수값인지 음수값인지를 기록한 추가 휠이 하나 더 있다. 가변 축 사이를 수평으로 달리는 랙, 기어 톱니 모양의 가장자리가 있는 긴 금속으로 저장소와 밀 사이에 숫자가 앞뒤로 전달된다. 작은 이동식 피니언기어는 주어진 가변 축을 랙에 연결하거나 연결되지 않은 상태로두기 위해 배치가되고 번호가 밀로 들어가는 경우 랙은 밀의 입구 축에도 연결이 가능하다. 거기에서 밀의다른 부분으로 전달이된다. 밀이 숫자에 대해 작동을 마치면 출구 축에 배치되고, 그런 다음 랙에 연결하여 결과를 저장하기 위해 선택한 가변 축에 번호를 전달한다. 밀은 부품을 연결하는 큰 중앙 휠 주위 왼쪽에 배열이 된다. 중앙 바퀴의 크기는 가로로 약 70cm, 밀의 전체는 각 방향으로 약 150cm 피트였다. 100 개의 가변 축이있는 저장소의 길이는 약 3m이다. 진입 축에는 자체 운반 메커니즘이 있는데, 덧셈과 뺄셈을 수행 한 다음 저장을 위해 출구 축으로 직접 전달이 가능하다. 곱셈이 나오면 처음 9개의 배수가 진입 축에 추가되고 T1에서 T9까지 표시된 테이블 축에 저장된다. 전체 곱셈 또는 나눗셈의 결과는 큰 중앙 바퀴의 왼쪽에있는 A 라고 표시된 두 개의 열에 형성된다. 이를 통해 중간 결과를 배정하고 밀 형식으로 유지할 수 있다 . 즉, 두 개의 40 자리 숫자를 곱하면 결과의 80 자리가 A 축에 유지 될 수 있다 . 이후 다른 40 자리 숫자로 나눈 결과에는 40 자리 값이 그대로 나오게된다. 분석 엔진의 주요 기계적 문제 중 하나는 운반문제이다. 처음에 찰스 배비지는 차분기관에서 사용하는 지연 순차 운반 방식을 사용했다. 여기에서 기본 주기 뒤에 별도의 운반주기가 뒤따르기에 운송사이클은 먼저 가장 낮은 자리에서 필요한 운송을 수행 한 다음 다음 높은 자리로 진행하는 식으로 진행되었다. 이 방법은 효과가 있었지만 각 자릿수에 대해 개별적으로 운반이 수행 되었기 때문에 결과를 계산하는데 매우 오랜시간을 필요로 했다. 그느 각 숫자 열에 30 또는 40 자리 숫자가있는 것으로 간주했기 때문에 계산속도는 훨씬 오래 걸릴 수 밖에 없었다. 따라서 단일 곱셈에는 수백 개의 별도 덧셈 단계가 필요하였고 계산시간을 줄이기에 톱니바퀴 기어의 운반속도가 중요했다. 그는 운반을 최적화하기 위해 다양한 접근 방식을 시도했다. 추가 하드웨어를 사용하면 운반 메커니즘이 기어가 필요한 위치에 도착해있고 하나 이상의 휠로 인해 톱니바퀴의 운반이 일련의 숫자에 걸쳐 전파 될 수있는 위치를 동시에 감지 할 수있다. 이는 축의 자릿수에 관계없이 모든 운반을 한 번에 수행 할 수 있다는 것이다. 운반제어를 예상하는 세부 사항을 작업하는 데 찰스 배비지는 수년이 걸렸다 그러나 작업 속도를 크게 높여 노력을 정당화 할 수 있었다. 다만 운반 메커니즘이 너무 복잡해서 각 추가 축에 대한 메커니즘이 허용되지 않다. 찰스 배비지는 단일 예상 캐리지 메커니즘이 중앙 휠을 통해 추가 컬럼과 자유롭게 연결될 수있는 디자인을 채택해야만 했다. 그때까지는 특수 하드웨어가 곱셈을 제공했다. 배비지는 곧 추가 축에서 추가 자체를 제거하고 중앙 바퀴를 통해 수행 할 수 있음을 발견했다. 추가 축은 단순히 개별 휠에 숫자를 저장했으며 필요에 따라 중앙 휠에서 연결하거나 분리 할 수 있다. 저장소는 오늘날의 스토리지 개념이고 작업이 수행되는곳은 밀이라 불렀다.[3]
내구성
해석기관은 수천 개의 바퀴가 달린 크고 복잡한 엔진에서 필수적이었으며, 동시에 한 축을 사용하여 구동하는 데 일정한 시간이 필요했다. 그 이유는 해석기관을 구축하고 작동하데 기어와 연결된 많은 부품들이 압력과 마모를 유발하기 때문이다. 현재 재현된 해석기관으로는 찰스 배비지가가 얼마나 효율적으로 내구성을 높이는데 성공했는지, 또는 그가 최상의 작업 각도를 확보하기 위해 다양한 기어의 종류들을 어떻게 배열했는지에 대한 여부는 알 수 없다. 다만 일부 피니언기어에서 계산값 오류가 발생한 부분이 있다. 엔진의 임시 프로세스에 분명히 필요한 움직임 중 하나는 주어진 샤프트 벨브 휠이 이전 작업에 따라 특정 위치로 이동되었을 때 통과하는 평면에서 날카로운 직선 모서리를 가져와야 한다. 샤프트의 축은 직선 가장자리에 위치한 톱니의 바퀴의 위치에 따라 일부는 오른쪽으로, 다른 일부는 왼쪽으로 밀리게된다. 이 작업은 기계가 원활하게 작동하기 위해 원래 제공되었는지 또는 나중에 작업에 의해 증가되었는지 여부에 관계없이 기계의 다른 부분의 간격이 결과에 수치 오류를 유발하지 않도록 보장하기 위해 필요하다. 이 작업의 원리는 일반적으로 해석기관 전체에서 사용되며, 구동 기어에 던지는 작업과 압력으로 밀리는 부품의 마모는 모두 기계의 내구성을 고려하는 데 중요한 요소를 형성한다. 또한 이 샤프트 벨브 막대는 필요할 때 기계의 일부를 잠그는 용도로 사용된다.[6]
주요인물

- 찰스 배비지는1791년 12월 26일 부유한 영국 은행가의 아들로 태어났다. 몸이 늘 허약하여서 어렸을적부터 많은 고생을 하며 자라왔다. 캠브리지 대학에 1810년 입학을 하게 되고 그 전까지 주로 가정교사에게 교육을 받았다. 찰스 배비지는 혼자 대수학을 깨우칠 정도로 수학에 관심이 많아 대학을통해 더 깊이 공부하고자 하였다. 그의 실력을 인정받아 25세에 영국학사원 회원으로 선정되었으며, 1828년에는 아이작 뉴턴과 스티븐 호킹이 역임한 것으로 유명한 캠브리지 루카스 석좌교수로 뽑히기도 하였다. 이러함에도 불구하고 찰스 배비지는 해석기관의 설계도 까지 내며 완성을 지을려 하였지만 결코 이루어지지 않았다.실제로 찰스 배비지는 사회적 지위, 정부 자금, 10 년간의 설계 및 개발, 최고의 영국 엔지니어링 기술이 있음에도 불구하고 완전한 기계를 구축하지 못했다. 그 이유는 여전히 논쟁의 여지가 있지만 실제 찰스 배비지는 매우 원칙적이며, 상대방을 쉽게 기분을 상하게했고 그가 적으로 받아 들인 사람들에 대해 맹렬한 대중 비판을 받아왔다. 해석기관의 부품하나하나 만들어야 해서 비용이 너무많이들고, 증기기관을 이용하기 때문에 압력과 톱니바퀴가 매우 정교해야 했으며, 영국 정부화의 자금협조, 지연, 신뢰성 실패 및 순수 과학과 응용 과학 사이의 문화적 차이가 실패 요소로 이야기된다. 찰스 배버지는 또한, 자신의 작업에 대해 강의하는 것을 싫어했고, 그의 엔진의 수학적 잠재력을 선포하거나 홍보하는데 매우 게을렀다. 결과적으로 엔진은 오류없는 테이블을 생성하기위한 실질적인 유용성에 대해 평가를 받았으며 당시의 전문가들은 새로운 테이블이 실제로 필요하다는 데 동의하지 않았고 일부는 기존 테이블이 이미 충분히 정확하고 거대한 기계를 만드는 데 드는 큰 자본 비용에 대한 경제적 정당성이 없다고 주장했다. 결국 그 시대에 주목받지 못한 기술이 되어버렸지만, 현재에 컴퓨터의 기초를 닦는 기술이 되었다.[7]
- 에이다 러브레이스(Ada Lovelace)는 오늘날 최초의 컴퓨터 프로그래머라 불린다. 찰스 배비지와의 만남을 통하여 차분기관과 해석기관에 대한 관심을 갖게 되고 해석기관 설계도를 통하여 가상 기계의 무궁무진한 가능성을 알아보고, 그 작동법을 만든 이가 있었는데 바로 에이다 러브레이스다. 이는 오늘날의 컴퓨터의 동작 원리는 물론이거니와 프로그래밍에 대한 기본적인 규칙과도 연관되는 부분이다. 찰스 배비지는 에이다를 “과학의 가장 추상적인 분야에 마술을 거는 마법사”이자 “활기찬 요정”이라고 불렀다. 찰스배비지가 컴퓨터의 하드웨어를 설계한 공학자라면 에이다 러브레이스는 소프트웨어를 짠 프로그래머인 셈이다. 해석기관은 그 두 사람의 두뇌 속에서만 작동하는 아주 특별한 기계였다. 해석기관에 관한 논문은 찰스 배비지가 1842년 이탈리아 토리노 대학을 방문해 해석기관에 대해 강의했을 때 참석했던 루이기 메나브레(Luigi Menabrea)가 강연 내용을 정리하고 기관의 구조를 설명한 논문(해석기관 개요)이 전부였다. 에이다는 프랑스어로 작성된 이 논문을 영어로 번역하고 주석을 달았는데, 주석의 길이가 본문의 2.5배에 달했다. 에이다는 A부터 G까지 9개의 주석을 달았는데, 이 주석에는 현대 컴퓨터 프로그래밍의 기본 개념을 담은 발상들이 담겨 있었다. 특히 주석 G에서 에이다는 해석기관이 복잡한 계산을 할 수 있음을 증명하기 위해 베르누이 수를 구하는 알고리즘을 만들어 냈다. 이는 컴퓨터에서 구현하기 위해 제작된 최초의 알고리즘이었고 이 때문에 그녀는 최초의 컴퓨터 프로그래머로 꼽힌다. 에이다는 이 기계가 수치 방정식 외에 다양한 정보를 처리할 수 있으며, 숫자가 아니라 문자나 음표 같은 다른 기호도 조작할 수 있으리라 믿었다. 당시 차분기관 또는 해석기관이 기계적인 방법으로 동작하고, 계산하는 원리가 그리 복잡하지 않았다는 점을 감안한다면 이러한 기계적인 구성 요소와 계산 원리에 대한 분리는 혁신적인 아이디어였으며, 동시에 오늘날까지 계승되고 있는 개념인 것이다에이다가 작성한 주석에는 서브루틴(Subroutine), 점프(Jump), 루프(Loop), 조건문(If then) 등 현대 컴퓨터 프로그램에서 사용되는 개념들이 들어 있었다. 당시 차분기관 또는 해석기관이 기계적인 방법으로 동작하고, 계산하는 원리가 그리 복잡하지 않았다는 점을 감안한다면 이러한 기계적인 구성 요소와 계산 원리에 대한 분리는 혁신적인 아이디어였으며, 동시에 오늘날까지 계승되고 있는 개념이다. 그럼에도 불구하고 이 논문을 끝으로 추가적인 논문 발표를 하지 못하고, 배비지와 함께 해석기관의 구현에 매달렸지만 결국 완전한 구현에는 실패함으로써 그녀는 더 이상 주목을 받지 못하였고, 1852년 36세에 암으로 짧은 생을 마감하게 된다.[8][9]이러한 에이다의 업적을 받들어 미국에서는 에이다라는 프로그래밍 언어를 계발했고 현재 미 국방부에서 사용하고 있다.
각주
- ↑ 더밋 튜링, 〈계산기는 어떻게 인공지능이 되었을까?〉, 《한빛미디어》, 2019-05-03
- ↑ John Graham-Cumming, 〈The 100-year leap〉, 《O'Reilly》, 2010-10-04
- ↑ 3.0 3.1 3.2 , 〈Analytical Engine〉, 《history-computer》,
- ↑ 반효경,〈운영 체제와 정보기술의 원리〉, 《이화여자대학교출판부》, 2008-01-31
- ↑ computerhope, 〈Punch card〉, 《computerhope》, 2020-08-02
- ↑ John Walker, 〈The Analytical Engine.〉, 《fourmilab》,
- ↑ LG CNS, 〈컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)'〉, 《엘지 씨엔에스》, 2015-11-09
- ↑ 이소영, 〈생활 속 과학탐구 - 최초의 프로그래머 에이다 러브레이스〉, 《국산업기술진흥협회》, 2018-04
- ↑ 시드니 파두아, 〈에이다, 당신이군요, 최초의 프로그래머 - 시드니 파두아〉, 《예스24 블로그》, 2018-01-28
참고자료
- John Walker, 〈The Analytical Engine.〉, 《fourmilab》
- 〈Analytical Engine〉, 《history-computer》
- 반효경,〈운영 체제와 정보기술의 원리〉, 《이화여자대학교출판부》, 2008-01-31
- John Graham-Cumming, 〈The 100-year leap〉, 《O'Reilly》, 2010-10-04
- LG CNS, 〈컴퓨터의 탄생, 시대를 앞서간 '찰스 배비지(Charles Babbage)'〉, 《엘지 씨엔에스》, 2015-11-09
- 시드니 파두아, 〈에이다, 당신이군요, 최초의 프로그래머 - 시드니 파두아〉, 《예스24 블로그》, 2018-01-28
- 이소영, 〈생활 속 과학탐구 - 최초의 프로그래머 에이다 러브레이스〉, 《국산업기술진흥협회》, 2018-04</ref>
- 더밋 튜링, 〈계산기는 어떻게 인공지능이 되었을까?〉, 《한빛미디어》, 2019-05-03
- computerhope, 〈Punch card〉, 《computerhope》, 2020-08-02</ref>
같이 보기

 위키원
위키원