BIP32
BIP32(Bitcoin Improvement Proposal 32)는 HD 지갑의 일반적인 형식과 HD 지갑을 구축하는 방법을 설명한 문서이다.
개요
BIP는 비트코인의 기술을 논의하기 위해 작성하거나 공개된 제안 양식이다. BIP32가 탄생하게 된 배경은 하나의 비트코인 주소보다 여러개의 비트코인 주소를 가지고 입출금을 하면 훨씬 더 안전하다는 것에서부터 출발하여 현재는 다양한 용도로 사용 가능하다. BIP32는 처음 HD 지갑(Hierarchical Deterministic Wallet)에 대한 구조를 제안했는데, HD 지갑은 BIP32 문서를 코드로 프로그래밍화한 것을 말한다. HD 지갑은 결정적 계층 구조 지갑으로 2진 트리처럼, 또는 부모-자손 관계를 이용해 끝없이 파생시킬 수 있는 지갑으로 BIP32 이외에도 BIP39, BIP44 등 여러 버전이 있으며 BIP39로 만들어진 프로그램은 이오스(EOS)나 다른 블록체인에서도 흔히 사용된다.[1]
등장배경
비트 코인을 받으려면 비트 코인 주소가 필요하다. 이 주소로받은 비트 코인을 보내려면 해당 개인 키가 필요하다. 따라서 비트 코 클라이언트는 적어도 하나의 비트 코 주소와 해당 개인 키가 유용해야합니다. 일반적으로, 비트 동전 지갑은 사용자가 여러 주소를 생성 할 수있게 한다. 복수의 주소를 사용하는 사용자는 하나의 주소만을 사용하는 사람보다 블록 체인을 감시하는 것을 더 어렵게하기 때문에 익명성에 도움이 된다. 요청시 주소 / 개인 키를 생성하는 초기 아이디어는 사용자가 주소를 요청할 때마다 임의로 새로운 주소를 효과적으로 생성하는 것이 었다. 이것이 bitcoin-qt가하는 방식이다. 이 방법의 단점 중 하나는 지갑이 모든 주소 / 키를 저장해야한다는 것이다. 따라서 사용자는 새로 생성 된 주소 / 키가 손실되지 않도록하기 위해 새 주소를 생성 할 때마다 지갑을 백업해야한다. BIP32 지갑은 사용자가 필요에 따라 새로운 주소를 생성 할 수 있지만 주소 / 키를 반복해서 백업 할 필요가 없다. 마술은 두 번째 주소 / 키가 무작위가 아니라 실제로 첫 번째 것의 파생물이고, 세 번째 것은 두 번째 파생 된 것입니다. 이 모든 것은 아무도 그 주소에서 어떤 주소도 추측 할 수 없도록하기 위해 일부 암호화에 의해 뒷받침 됩니다. 첫 번째 개인 키가 없어도 지갑을 사용할 수 있습니다.
종류
기본구조
Bitcoin 참조 클라이언트는 임의로 생성 된 키를 사용합니다. 매 트랜잭션마다 백업이 필요하지 않도록 (기본적으로) 100 개의 키가 예약 키 풀에 캐시됩니다. 하지만이 지갑은 여러 시스템에서 동시에 공유하고 사용할 수 없습니다. 그들은 지갑 암호화 기능을 사용하고 비밀 번호를 공유하지 않음으로써 개인 키를 숨기도록 지원하지만 그러한 "중성화 된"지갑은 공개 키를 생성 할 수있는 능력을 잃어 버립니다.
결정 론적 지갑은 빈번한 백업을 필요로하지 않으며, 타원 곡선 수학은 개인 키를 공개하지 않고 공개 키를 계산할 수있는 스키마를 허용합니다. 이것은 예를 들어 webshop 비즈니스가 웹 서버가 (수신 된 자금을 소비하는 데 필요한) 해당 개인 키에 대한 액세스를 제공하지 않고 웹 서버가 각 주문 또는 각 고객에 대해 새로운 주소 (공개 키 해시)를 생성하도록 허용합니다.
그러나 결정 론적 지갑은 일반적으로 키 쌍의 단일 "체인"으로 구성됩니다. 단 하나의 체인이 있다는 사실은 지갑을 공유하는 것이 모두 또는 전혀 기초가 없다는 것을 의미합니다. 그러나 경우에 따라 일부 공개 키만 공유하고 복구 할 수 있기를 원합니다. 웹샵의 예에서 웹 서버는 판매자의 지갑의 모든 공개 키에 액세스 할 필요가 없습니다. 예를 들어 판매자가 돈을 지불 할 때 생성되는 변경 주소가 아닌 고객의 지불을받는 데 사용되는 주소에만 적용됩니다. 계층 적 결정 론적 지갑은 단일 루트에서 파생 된 여러 개의 키 쌍 체인을 지원함으로써 이러한 선택적 공유를 허용합니다.
협약
이 텍스트의 나머지 부분에서는 Bitcoin에서 사용되는 공개 키 암호화, 즉 secp256k1 ( http://www.secg.org/sec2-v2.pdf )에서 정의한 필드 및 곡선 매개 변수를 사용하는 타원 곡선 암호화를 가정합니다 . 아래 변수는 다음 중 하나입니다.
- 곡선의 차수를 n으로 나타내는 정수입니다.
- 커브상의 점의 좌표입니다.
- 바이트 시퀀스.
두 좌표 쌍의 더하기 (+)는 EC 그룹 연산의 적용으로 정의됩니다. 연결 (||)은 1 바이트 시퀀스를 다른 시퀀스에 추가하는 작업입니다. 표준 변환 함수로 다음과 같이 가정합니다.
- point (p) : secp256k1 기준점의 EC 포인트 곱셈 (EC 그룹 연산의 반복 적용)에서 나온 좌표 쌍을 정수 p로 반환합니다.
- ser 32 (i) : 32 비트 부호없는 정수 i를 4 바이트 시퀀스로 최상위 바이트 먼저 serialize합니다.
- ser 256 (p) : 정수 p를 32 바이트 시퀀스로 최상위 바이트 먼저 serialize합니다.
- ser P (P) : SEC1의 압축 형식 (0x02 또는 0x03)을 사용하여 좌표 쌍 P = (x, y)를 바이트 시퀀스로 직렬화합니다. ser 256 (x). 여기서 헤더 바이트는 생략 된 y 좌표의 패리티에 따라 다릅니다.
- 256 (p) 파싱 : 32 비트 시퀀스를 최상위 바이트 인 256 비트 숫자로 먼저 해석합니다.
확장키
다음에서는 상위 키에서 여러 하위 키를 유도하는 함수를 정의합니다. 이것들이 키 자체에만 의존하는 것을 막기 위해서 우리는 우선 256 비트의 엔트로피로 개인 키와 공개 키를 확장합니다. 체인 코드라고하는이 확장은 해당 개인 키와 공개 키에서 동일하며 32 바이트로 구성됩니다.
우리는 확장 개인 키를 (k, c)로 표현하고, k는 일반 개인 키를, c는 체인 코드를 나타낸다. 확장 공개 키는 (K, c), K = 포인트 (k) 및 체인 코드로 표현된다.
각 확장 키에는 2 31 개의 일반 자식 키와 2 31 개의 강화 된 자식 키가 있습니다. 이러한 각 하위 키에는 색인이 있습니다. 통상의 아이 키는 0 ~ 2 31 -1의 인덱스를 사용 합니다. 강화 된 자식 키는 인덱스 2 31 에서 2 32 -1을 사용합니다. 강화 된 키 인덱스에 대한 표기법을 쉽게하기 위해 숫자 i H 는 i + 2 31을 나타냅니다 .
하위 키 유도 (CKD) 함수
부모 확장 키 및 인덱스 i가 주어지면, 대응하는 자식 확장 키를 계산하는 것이 가능하다. 이렇게하는 알고리즘은 아동이 강화 된 키인지 아닌지 (또는 i ≧ 2 31 인지 여부)와 개인 키 또는 공개 키에 대해 이야기하는지 여부에 따라 다릅니다 .
개인 부모 키 → 개인 자식 키 함수 CKDpriv ((k par , c par ), i) → (k i , c i )는 부모 확장 개인 키에서 자식 확장 개인 키를 계산한다 :
- i ≥ 2 31 (아이가 강화 된 키인지 여부)를 확인하십시오.
그렇다면 : HMAC-SHA512 (Key = c par , Data = 0x00 || ser 256 (k par ) || ser 32 (i)) 라고합시다 . (참고 : 0x00은 33 바이트 길이가되도록 개인 키를 채 웁니다.) 그렇지 않다면 (HMAC-SHA512) (Key = c par , Data = ser P (point (k par )) || ser 32 (i)).
- I를 두 개의 32 바이트 시퀀스, I L 과 I R 로 분할 합니다.
- 반환 된 자식 키 (K)의 난 파싱 인 256 (I의 L ) + (K)의 액면 (mod n)을 계산한다.
- 반환 된 체인 코드 c i 는 I R 입니다.
- 구문 256 (I L ) ≥ n 또는 k i = 0 인 경우 결과 키는 유효하지 않으며 i는 다음 값으로 진행해야합니다. (참고 : 2 127의 확률은 1보다 낮습니다 .)
HMAC-SHA512 기능은 RFC 4231에 명시되어 있습니다. 공용 상위 키 → 공용 하위 키 함수 CKDpub ((K의 파 는 C 파가 ), 나) → (K는 난 , C, I ) 아이 공개 키 확장 부모로부터 공개 키를 확장 연산한다. non-hardened 자식 키에 대해서만 정의됩니다.
- i ≥ 2 31 (아이가 강화 된 키인지 여부)를 확인하십시오.
- 그렇다면 (단단한 자식) : 반환 실패
- 그렇지 않다면 (정상 아동) : HMAC-SHA512 (Key = c par , Data = ser P (K par ) || ser 32 (i)) 라고합시다 .
I를 두 개의 32 바이트 시퀀스, I L 과 I R 로 분할 합니다.
- 반환 된 자식 키 K가 나는 지점 (파싱 인 256 (I의 L을 )) + K의 파 .
- 반환 된 체인 코드 c i 는 I R 입니다.
- 파싱 256 (I L ) ≥ n 또는 K i 가 무한대의 점인 경우 결과 키는 유효하지 않으며 i는 다음 값으로 진행해야합니다.
개인 부모 키 → 공개 자식 키 함수 N ((k, c)) → (K, c)는 확장 된 개인 키에 상응하는 확장 공개 키를 계산합니다 ( "중립"버전은 트랜잭션 서명 기능을 제거합니다).
- 반환 된 키 K는 point (k)입니다.
- 반환 된 체인 코드 c는 전달 된 체인 코드입니다.
상위 개인 키의 공용 하위 키를 계산하려면 다음을 수행하십시오.
- N (CKDpriv ((k par , c par ), i)) (항상 작동 함).
- CKDpub (N (k par , c par ), i) (강화되지 않은 자식 키에서만 작동).
키가 동일하다는 사실은 강화되지 않은 키를 유용하게 만드는 것입니다 (개인 키를 모르는 상태에서 지정된 부모 키의 자식 공개 키를 파생시킬 수 있음). 또한 강화 된 키와 구별되는 점도 있습니다. 보안이 강화되지 않은 키 (더 유용함)를 항상 사용하지 않는 이유는 보안입니다. 자세한 내용은 추가 정보를 참조하십시오. 공개 부모 키 → 개인 자식 키 이건 불가능 해.
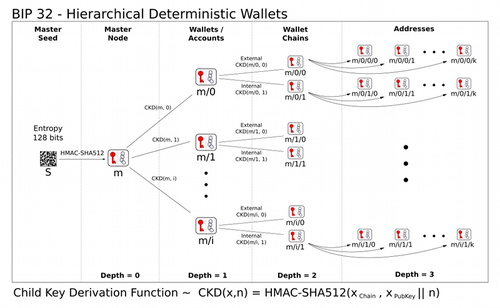
키트리
다음 단계는 여러 개의 CKD 구성을 계단식으로 배열하여 나무를 만드는 것입니다. 우리는 하나의 루트, 마스터 확장 키로 시작합니다. i의 여러 값에 대해 CKDpriv (m, i)를 평가하면 레벨 1 파생 노드 수를 얻을 수 있습니다. 이들 각각은 다시 확장 키이므로 CKDpriv도 해당 키에 적용 할 수 있습니다.
표기법을 줄이기 위해 우리는 CKDpriv (CKDpriv (CKDpriv (m, 3 H ), 2), 5)를 m / 3 H / 2 / 5로 씁니다 . 공개 키와 마찬가지로 CKDpub (CKDpub (CKDpub (M, 3), 2), 5)를 M / 3 / 2 / 5로 씁니다. 결과적으로 다음과 같은 ID가 생성됩니다.
- (m / a) / b / c = N (m) / a / b / c = M / a / b / c = N (m / 기음.
- N (m / aH / b / c) = N (m / aH / b) / c = N (m / aH ) / b / c.
그러나 N (m / a H )은 N (m) / a H 로 다시 쓸 수 없습니다 . 왜냐하면 후자가 불가능하기 때문입니다. 트리의 각 리프 노드는 실제 키에 해당하는 반면 내부 노드는 키의 컬렉션에 해당합니다. 잎 노드의 체인 코드는 무시되며 내장 된 개인 키나 공개 키만 관련됩니다. 이 구성으로 인해 확장 개인 키를 알고 있으면 모든 자손 개인 키와 공개 키를 재구성 할 수 있고 확장 공개 키를 알고 있으면 모든 하위 키가 아닌 공개 키를 재구성 할 수 있습니다.
키 식별자
확장 된 키는 체인 코드를 무시하고 직렬화 된 ECDSA 공개 키 K의 Hash160 (SHA256 이후의 RIPEMD160)으로 식별 할 수 있습니다. 이것은 전통적인 Bitcoin 주소에서 사용되는 데이터와 정확하게 일치합니다. 이 데이터를 base58 형식으로 표현하는 것은 권장하지 않습니다. 이는 주소 방식으로 해석 될 수 있으므로 (지갑 소프트웨어 자체가 체인 키에 대한 지불을 수락하지 않아도되기 때문입니다).
식별자의 처음 32 비트는 키 지문이라고합니다.
직렬화 형식
확장 공개 키와 비공개 키는, 다음과 같이 직렬화됩니다.
- 4 바이트 : 버전 바이트 (mainnet : 0x0488B21E public, 0x0488ADE4 private, testnet : 0x043587CF public, 0x04358394 private)
- 1 바이트 : 깊이 : 마스터 노드의 경우 0x00, 레벨 1 파생 키의 경우 0x01 ...
- 4 바이트 : 부모 키의 지문 (마스터 키인 경우 0x00000000)
- 4 바이트 : 자식 번호. 이것은 x 32 i (i) x i = x par / i이고 x i 는 키가 직렬화 된 것입니다. (마스터 키인 경우 0x00000000)
- 32 바이트 : 체인 코드
- 33 바이트 : 공개 키 또는 개인 키 데이터 (공개 키의 경우 ser P (K), 개인 키의 경우 0x00 || ser 256 (k))
이 78 바이트 구조는 처음에 32 개의 체크섬 비트 (이중 SHA-256 체크섬에서 파생 됨)를 추가 한 다음 Base58 표현으로 변환하여 Base58의 다른 Bitcoin 데이터와 같이 인코딩 할 수 있습니다. 그 결과 Base58로 인코딩 된 최대 112 자의 문자열이 생성됩니다. 버전 바이트를 선택했기 때문에 Basenet은 testnet의 메인 트루넷 "xprv"또는 "xpub", "tprv"또는 "tpub"로 시작합니다. 부모의 지문은 소프트웨어에서 부모 노드와 자식 노드를 빠르게 탐지하는 역할을하며 소프트웨어는 충돌을 처리해야합니다. 내부적으로 전체 160 비트 식별자를 사용할 수 있습니다.
직렬화 된 확장 공개 키를 임포트 할 때, 구현은 공개 키 데이터의 X 좌표가 곡선상의 한 점과 일치하는지 여부를 검증해야합니다. 그렇지 않은 경우 확장 공개 키가 유효하지 않습니다.
참고자료
같이 보기

 위키원
위키원