방향성 비순환 그래프

탱글(Tangle) 알고리즘

탱글(Tangle) 알고리즘

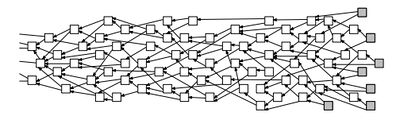
방향성 비순환 그래프(DAG; Directed Acyclic Graph)란 개별 요소들이 특정한 방향을 향하고 있으며, 서로 순환하지 않는 구조로 짜여진 그래프를 말한다. 간략히 DAG(대그)라고 쓴다. 아이오타(IOTA)에 적용된 탱글 알고리즘과 헤데라 해시그래프에 적용된 해시그래프 등이 있다.

방향성 비순환 그래프에서 개별 요소들은 블록체인처럼 여러 개의 트랜잭션을 하나의 블록으로 묶지 않고, 각 개별 요소들끼리 상호 연결되어 있다. 방향성 비순환 그래프는 시간적으로 이전 트랜잭션에 대해 그 이후 트랜잭션이 검증하는 구조로 되어 있다. 시간 t를 기준으로 그 다음에 이어질 시간 t+1의 상태를 추측하기 위해 마르코프 체인 몬테 카를로(MCMC; Markov Chain Monte Carlo) 알고리즘을 사용한다.

개요

방향성 비순환 그래프는 DAG(대그)라고도 하며 Directed Acyclic Graph의 약자이다. 직역 그대로 한 방향으로 이어지지만, 순환은 하지 않는 그래프 이다. '방향성 비 사이클' 그래프이며 방향을 가지지만 루프를 생성하지 않는 그래프라는 의미이다. 여기서 루프, 또는 사이클이란 자기 자신에서 출발해 다시 자신에게 돌아오는 경로를 말하며 비 사이클이므로 이러한 경로가 없어야 한다.

a라는 최초의 거래내역을 그 뒤의 b, c, d, e가 검증한다. 또한 그 뒤의 g, f가 b, c, d, e를 검증한다. g, f 는 동시에 a 를 비간접적으로 검증했다고 볼 수 있다.

이런식으로 꼬리에 꼬리를 물며 추가되는 트랙젝션들이 앞의 트랜젝션들을 직, 간접적으로 검증하게 되면서 네트워크가 형성된다. 이러한 직, 간접 검증이 누적된 트랜젝션은 검증이 완료되었다고 보고 확정이 된다. 이 것은 거래가 완료되었다고 볼 수도 있다.

아이오타에서는 이 구조를 탱글이라고 부르는데, 이 탱글에 사람들이 참여하면 참여할 수록 검증이 더욱 많이 되므로, 더 신뢰할 수 있는 시스템이 된다. 또한 사람들이 이 시스템에 많이 참여할수록 확저되는 트랜젝션들이 늘어남으로써 확장성의 문제도 해결할 수 있다.

이러한 DAG 합의 구조를 쓰는 코인에 IOTA, HSR, ADK 등이 있다.

특징

방향성 비순환 그래프(Directed Acyclic Graph)는 블록체인 3.0단계이다. DAG 알고리즘을 적용한 기술은 블록체인 3.0 시대를 이끌 기술로 꼽히고 있다. 세대라고 표현해도 나쁘지 않다. Melanie Swan이 쓴 Blockchain에는 블록체인 발전 단계를 3단계로 나누어 설명 하였다.

• 블록체인 1.0 단계 : 통화나 화폐로서의 목적을 수행하기 위한 논의가 이루어지는 단계. 현재 우리나라에서 격론이 벌어지고 있는 단계라고 볼 수 있으며 이 단계는 주로 비트코인의 이름으로 진행되는 단계라고 한다.
• 블록체인 2.0 단계 : 금융, 경제 분야에서 큰 변화를 가져오는 단계. 거래나 계약에 있어서 국가나 정부와 같이 중앙집권적인 조직이나 중개인을 거치지 않고 상호 계약으로도 충분히 신뢰를 가지고 이루어지는 과정을 그려볼 수 있다. 이더리움의 Smart Contract가 대표적인 사례로 언급된다.
• 블록체인 3.0 단계 : 단순한 특정 분야를 넘어서 사회 전반에 블록체인 기술이 영향을 미치는 단계. 정부 정책을 활용하는 단계에서도, 의료계에서도, 운송업에서도, 스포츠나 예술 분야에서도 이러한 기술들이 효과적으로 적용될 수 있다. 3.0 단계에서는 탈중앙화, 보안, 공개된 장부 들을 바탕으로 하는 블록체인 기술의 특징으로 사회 구성원 개개인에 의한 신뢰를 형성한다.

사실 어떤 것도 아직 구체화된 것은 없지만 블록체인 기술의 청사진을 보았을 때 이 기술을 바탕으로 수많은 프로젝트가 사회를 바꾸기 위한 노력을 진행하고 있는 것은 누구나 알고 있을 것이다. 그 가운데 블록체인 3.0 단계 실현을 위한 훌륭한 기술로 꼽히는 것이 DAG 이다.

DAG는 올바른 기능을 위해 정확하게 사용된다면 블록체인의 확장성 딜레마를 극복 할 수 있다. 모든 거래가 이전의 두 가지 거래를 수락하기 때문에네트워크의 속도는 그 차원에 따라 기하 급수적으로 증가한다. 블록이없고 그 채굴이 없다는 것은 일반적으로 거래가 덩어리 진"이 아니라 "온더 플라이 (ON-THE-FLY)"로 진행된다는 것을 의미하며

활용 사례

방향성 비순환 그래프(DAG)를 사용하는 곳은 다음과 같다.

• 아이오타(IOTA)
• 아이오티체인(IoT Chain)
• 하이퍼캐시(Hcash)
• 해시그래프(hashgraph)
• 하이콘(Hycon)
• 팬텀(Fantom)

장점

사용자가 많을 수록 빠르다

DAG 알고리즘이 적용된 기술은 불록이 없기 때문에 채굴자들의 트랜잭션 승인을 기다릴 필요가 없다. 블록 생성 없이 트랜잭션이 다른 트랜잭션을 검증하기 때문에 매우 빠른 속도로 절차가 수행되며 검증과정이 병렬적으로 이루어지기 때문에 트랜잭션이 많을 수록 즉, 사용하자가 많을 수록 검증절차는 더욱 빨라진다.

수수료가 없다

POW 방식의 암호화폐를 전송하는데 드는 수수료는 대체로 채굴에 대한 보상으로 발생한다. 하지만 블록의 개념이 없는 DAG 방식은 채굴자가 없기 때문에 기본적으로 수수료 또한 발생하지 않는다.

확작성 문제가 없다

일반적인 블록체인에서는 사용량이 많아질 수록 블록 대비 트랜잭션 수가 넘쳐나는 병목현상이 발생하지만 DAG는 사용량이 많아질 수록 새로운 트랜잭션을 검증할 이전 트랜잭션이 많아지므로 오히려 검증의 신뢰도와 속도는 증가한다.

참고자료

• 아이오타 백서 - Serguei Popov, "The Tangle" Version 1.4.3, 2018-04-30
• prosong77, 〈DAG (방향성 비순환 그래프) 아이오타의 합의구조 (IOTA)〉, 《steemit》
• 조은써비스, 〈블록체인 3.0 세대를 이끌 기술, DAG(Directed Acyclic Graph)〉, 《네이버블로그》, 2019-04-29
• 〈DAG가 Blokchain 확장 성 문제를 해결하는 방법〉, 《코인뉴스》, 2018-05-14

같이 보기

• 탱글
• 해시그래프
• 마르코프 체인 몬테 카를로

이 방향성 비순환 그래프 문서는 블록체인 기술에 관한 토막글입니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 이 문서의 내용을 채워주세요.

블록체인 : 블록체인 기술 □■⊕, 합의 알고리즘, 암호 알고리즘, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 블록체인 기술 Bech32 • BTP • DRC-20 • EIP • IPFS • KRC-20 • NFT 마켓플레이스 • P2P • P2PKH • P2SH • PFP • PUF • SPV • TPS • TRC-20 • UTXO • 가나슈 • 가명성 • 가스 • 가십 • 가십 프로토콜 • 개념증명(PoC) • 검증가능지연함수(VDF) • 게스 • 고스트 프로토콜 • 공공예산 • 글로벌신뢰인공지능 • 대체가능토큰 • 대체불가토큰(NFT) • 도지더리움 브릿지 • 디지털 자산 • 디지털 희소성 • 라운드 • 라운드 로빈 • 라이트하우스 • 랜덤 • 레그테크 • 레이든 • 리카르디안 계약 • 린스타트업 • 마스터키 • 마스트 • 메인넷 • 멜팅 • 믹싱 • 민팅 • 밈블윔블 • 반감기 • 베타넷 • 변경불가성 • 브릿지 • 블록체인 생태계 • 블록체인 클라우드 서비스(BaaS) • 블룸필터 • 비블록체인 • 비앱 • 비콘체인 • 비트코인코어 • 빤통경제 • 수정 고스트 프로토콜 • 스냅샷 • 스마트 계약 • 스마트 브리지 • 스웜프로토콜 • 스크립트퍼브키 • 스테이킹 • 스텔스 주소 • 스핀오프코인 • 슬래싱 • 시크릿 컨트랙트 • 심플 컨트랙트 • 아토믹스왑 • 암호경제(크립토 이코노미) • 앤드어스체인인공지능 • 앵커링 • 언스테이킹 • 에어드랍 • 에폭 • 오프체인 오더락 • 오피리턴 • 옵코드 • 원토큰 문제 • 웨이 • 위스퍼 프로토콜 • 위임 • 유니스왑 • 유동성 • 이더리움 가상머신(EVM) • 이더리움 클라이언트 • 이중지불 • 익명성 • 인증된 익명 아이디 • 인터레저 프로토콜(ILP) • 자산화 • 잠금 스크립트 • 최소기능제품(MVP) • 컨소시엄 블록체인 • 컬러드코인 • 코인셔플 • 코인소각 • 코인에이지 • 코인조인 • 코인토싱 • 크립토노트 • 키스토어 • 타임락 • 테스트넷 • 토다 • 토큰 이코노미 • 토큰화 • 튜링완전 • 튜링불완전 • 트랜잭션 아이디(TxID) • 트러스트 컨트랙트 • 트루빗 • 트릴레마 • 파워 • 파티셔닝 • 퍼블릭 블록체인 • 페널티 • 프라이버시 • 프라이빗 블록체인 • 플랫폼 • 플러딩 • 피어 • 피투피(P2P) • 하이브리드 블록체인 • 합의 • 해시락 • 해시타임락(HTLC) • 해제 스크립트 • 확장성 해시 레인보우 테이블 • 매핑 • 머클경로 • 머클루트 • 머클트리 • 분산해시테이블(DHT) • 블록해시 • 스큐드 머클트리 • 온라인툴즈 • 이전블록해시 • 카뎀리아 • 해시 • 해시레이트 • 해시맵 • 해시충돌 • 해시테이블 • 해시파워 • 해시함수 • 해싱 블록 고아블록 • 그래핀 • 논스 • 마이크로블록 • 베이킹 • 북키퍼 • 브랜치블록 • 브로드캐스팅 • 블록 • 블록높이 • 블록바디 • 블록생성자 • 블록정보 • 블록타임 • 블록헤더 • 비츠 • 세그윗 • 엉클블록 • 완결성 • 제네시스블록 • 타임스탬프 • 프룻 • 프룻체인 체인 더블체인 • 라이트닝 네트워크 • 라이트닝 루프 • 루트체인 • 루프체인 • 메인체인 • 방향성 비순환 그래프(DAG) • 베리파이어블 프루닝 • 블록격자 • 블록체인 • 사용자 활성화 소프트포크(UASF) • 사용자 활성화 하드포크(UAHF) • 사이드체인 • 서브체인 • 소프트포크 • 오페라체인 • 오프체인 • 온체인 • 인터체인 • 차일드체인 • 체인 • 탱글 • 테스트체인 • 토카막 네트워크 • 포크 • 포크체인 • 퓨어체인 • 프로덕트체인 • 프루닝 • 프리포크 • 플라즈마 알고리즘 • 플라즈마캐시 • 플래시 계층 • 하드포크 • 해시그래프 • 홀로체인 노드 검증인(밸리데이터) • 기본노드 • 노드 • 라이트노드 • 랜덤노드 • 마스터노드 • 베이킹노드 • 보조노드 • 보증노드 • 슈퍼노드(슈퍼대표, 대표노드) • 슬롯 • 슬롯리더 • 엔드포인트노드(레인저노드) • 의회 네트워크 • 작업노드 • 종단노드 • 종자노드(시드노드) • 중계노드 • 지갑노드 • 채굴노드(마이닝노드) • 쿼럼 • 풀노드 • 합의노드 샤딩 네트워크 샤딩 • 데이터베이스 샤딩 • 동적샤딩 • 샤드 • 샤딩 • 스테이트 샤딩 • 알고리즘 샤딩 • 적응형 상태 샤딩 • 체인샤딩 • 트랜잭션 샤딩 채굴 병합채굴 • 사전채굴 • 에이식(ASIC) • 에이식부스트 • 에이식 저항 • 일드파밍 • 채굴 • 채굴 난이도 • 채굴량 • 탄소감축채굴 • 페어런치 탈중앙화 TVL • 거버넌스 • 게임파이 • 다오(DAO) • 다이코(DAICO) • 닥(DAC) • 닥스(DAX) • 덱스(DEX) • 디앱(DApp) • 디지오(DGO) • 디튜브 • 디파이(DeFi) • 분산경제 • 분산원장(DLT) • 분산 클라우드 • 소셜파이 • 씨파이(C-Fi) • 오프체인 거버넌스 • 온체인 거버넌스 • 원장 • 준중앙화 • 중앙화 • 탈중앙화 • 탈중앙화 TPS • 탈중앙화 조직(DO) • 탈중앙화 지수(DQ) 분산아이디 DIDs • IETF • ToIP • 검증가능한 자격증명 • 검증인 • 디지털아이덴티티재단 • 발급자 • 보유자 • 분산아이디(DID) • 분산아이디 기관 • 분산아이디 인증(DID Auth) • 아이온 • 자기주권 • 자기주권신원 • 최소화된 자격증명 데이터 • 탈중앙화 키관리시스템 • 통합해석기 오라클 상호인증 블록체인 • 오라클 • 오라클 머신 • 오라클 문제 • 오라클 서비스 • 중간자 BIP BIP • BIP9 • BIP16 • BIP32 • BIP39 • BIP43 • BIP44 • BIP47 • BIP49 • BIP63 • BIP70 • BIP84 • BIP141 • BIP148 ERC ERC • ERC-20 • ERC-165 • ERC-223 • ERC-621 • ERC-721 • ERC-777 • ERC-827 • ERC-884 • ERC-998 • ERC-1155 • ERC-1404 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반