방사신경망

방사신경망

방사신경망(Radial basis function network)은 방사 함수를 활성화 함수로 사용하는 인공신경망이다. 네트워크의 출력은 입력과 뉴런 매개 변수의 방사 함수의 선형 결합이다. 방사신경망은 함수 근사치, 시계열 예측, 분류 및 시스템 제어를 포함하여 많은 용도에 쓰인다.

개요

방사신경망은 왕립신호 및 레이더 연구소의 연구원인 브룸헤드(Broomhead)와 로우(Lowe)에 의해 1988년 논문에서 처음 공식화되었다. 방사신경망은 다차원 공간의 보간법에 강력한 능력을 가지고 있는 신경망으로 방사형 구조를 기본으로 하는 네트워크를 가지고 있다. 1개의 은닉층에는 확률 가우시안이 적용되어 있다. 방사신경망은 은닉층이 1개이며, 유클리디안 거리를 사용한다. 또한 역전파 알고리즘을 사용하고, 안정성 판별이 가능하다는 네 가지의 특징이 있다. 방사신경망은 보편적인 근사 및 빠른 학습 속도로 인해 다른 신경망과 구별된다. 방사신경망은 입력 계층, 숨겨진 계층 및 출력 계층의 세 계층으로 구성된 피드 포워드 신경망의 한 유형이다. 이러한 각 계층에는 서로 다른 작업이 존재한다. 계산된 오류가 원하는 값 또는 학습 반복 횟수에 도달하면 방사신경망 모델의 학습이 종료된다. 그리고 히든 레이어에 특정 수의 노드가 있는 방사신경망이 선택된다. 이는 가우스 함수 계산 단위의 전달 함수로 사용된다. 경우에 따라 일반적으로 방사신경망이 다층퍼셉트론에 비해 훈련 종료에 도달하는 데 더 적은 시간이 필요하다는 것이 관찰된다. 선택된 다층퍼셉트론 및 방사신경망은 나중에 새로운 테스트 조건에서 다음 장에서 검토된다. 그리고 모델 예측과 실험적 관찰 사이의 일치를 조사하고 두 모델의 결과를 비교한다. 그런 다음 최소 계산 오류를 기반으로 최종 모델이 선택된다.

구조

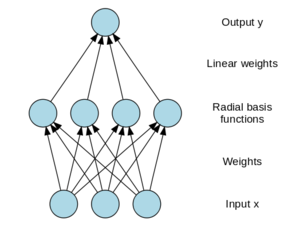
방사신경망은 일반적으로 입력 계층, 비선형 방사 기저 함수 활성화 기능이 있는 숨겨진 계층, 선형 출력 계층의 세 가지 계층을 가진다. 입력은 실수 $\mathbf {x} \in \mathbb {R} ^{n}$의 벡터로 모델링할 수 있다. 그러면 네트워크의 출력은 입력 벡터 $\varphi :\mathbb {R} ^{n}\to \mathbb {R}$의 스칼라 함수가 되며, $\varphi (\mathbf {x} )=\sum _{i=1}^{N}a_{i}\rho (||\mathbf {x} -\mathbf {c} _{i}||)$로 주어진다.

여기에서 $N$은 숨겨진 층에 있는 뉴런의 수, $\mathbf {c} _{i}$는 뉴런 $i$의 중심 벡터, $a_{i}$는 선형 출력 뉴런에 있는 뉴런 $i$의 무게다. 중심 벡터로부터의 거리에만 의존하는 함수는 그 벡터에 대해 방사적으로 대칭되므로, 명칭은 방사상 기준 함수다. 기본적인 형태에서 모든 입력은 각각의 숨겨진 뉴런과 연결된다. 규범은 마할라노비스 거리가 패턴 인식으로 더 잘 수행되는 것처럼 보이지만 전형적으로 유클리드 거리로 취하며 방사상 기준 함수는 일반적으로 가우스 함수로 취해진다.

 $\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}=\exp \left[-\beta \left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]$

가우스 기본 함수는 다음 식을 의미하는 중앙 벡터에 국부적이다.

 $\lim _{||x||\to \infty }\rho (\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert )=0$

즉, 하나의 뉴런의 매개변수 변경은 그 뉴런의 중심에서 멀리 떨어져 있는 입력 값에 작은 영향만 미친다. 활성화 함수의 형태에 대한 특정한 가벼운 조건을 고려할 때, 방사신경망은 $\mathbb {R} ^{n}$의 컴팩트 부분 집합에 있는 범용 근사치들이다. 이것은 충분한 숨겨진 뉴런을 가진 방사신경망이 임의의 정밀도로 폐쇄되고 경계된 집합의 어떤 연속적인 기능도 대략적으로 맞출 수 있다는 것을 의미한다.

매개변수 $a_{i}$, $\mathbf {c} _{i}$ 및 $\beta _{i}$는 $\varphi$와 데이터 사이의 적합성을 최적화하는 방법으로 결정된다.

정규화

정규화 구조

위의 비정형 아키텍처 외에도 방사신경망을 표준화할 수 있다.

 $\varphi (\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\sum _{i=1}^{N}a_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}=\sum _{i=1}^{N}a_{i}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}$

정규화는 위의 식으로 매핑된다.

$u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{j=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{j}\right\Vert {\big )}}}$

위의 식은 '정규화된 방사형 기저 함수'라고 한다.

정규화를 위한 이론적 동기

확률적 데이터 흐름의 경우 이 구조에 대한 이론적 정당성이 있다. 먼저 결합 확률 밀도에 대한 확률적 커널 근사치를 가정한다.

 $P\left(\mathbf {x} \land y\right)={1 \over N}\sum _{i=1}^{N}\,\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\,\sigma {\big (}\left\vert y-e_{i}\right\vert {\big )}$

위 식에서 가중치 $\mathbf {c} _{i}$ 및 $e_{i}$는 데이터의 예시이며, 커널이 정규화된

 $\int \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}\,d^{n}\mathbf {x} =1$
 $\int \sigma {\big (}\left\vert y-e_{i}\right\vert {\big )}\,dy=1$

위의 두 식을 필요로 한다.

입력 및 출력 공간의 확률 밀도는 $P\left(\mathbf {x} \right)=\int P\left(\mathbf {x} \land y\right)\,dy={1 \over N}\sum _{i=1}^{N}\,\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}$이고

입력 $x$에 대한 $y$의 기대치는 $\varphi \left(\mathbf {x} \right)\ {\stackrel {\mathrm {def} }{=}}\ E\left(y\mid \mathbf {x} \right)=\int y\,P\left(y\mid \mathbf {x} \right)dy$ 이다.

위 식에서 $P\left(y\mid \mathbf {x} \right)$는 $y$의 주어진 $x$의 조건부 확률이다.

조건부 확률은 $\varphi \left(\mathbf {x} \right)=\int y\,{\frac {P\left(\mathbf {x} \land y\right)}{P\left(\mathbf {x} \right)}}\,dy$를 산출하는 베이즈 정리 $P\left(y\mid \mathbf {x} \right)={\frac {P\left(\mathbf {x} \land y\right)}{P\left(\mathbf {x} \right)}}$ 을 통한 접합 확률과 관련이 있다.

 $\varphi \left(\mathbf {x} \right)={\frac {\sum _{i=1}^{N}e_{i}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}}}=\sum _{i=1}^{N}e_{i}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}$

통합이 수행되면 위 식이 된다.

로컬 선형 모형

때때로 로컬 선형성 모델을 포함하도록 구조를 확장하는 것이 편리하다. 이 경우 구조는 비정상화 및 정규화 사례에서 각각 아래의 두 식이 된다.

 $\varphi \left(\mathbf {x} \right)=\sum _{i=1}^{N}\left(a_{i}+\mathbf {b} _{i}\cdot \left(\mathbf {x} -\mathbf {c} _{i}\right)\right)\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}$
 $\varphi \left(\mathbf {x} \right)=\sum _{i=1}^{N}\left(a_{i}+\mathbf {b} _{i}\cdot \left(\mathbf {x} -\mathbf {c} _{i}\right)\right)u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )}$

$\mathbf {b} _{i}$는 결정해야 할 가중치들이다. 더 높은 차수의 선형 항도 가능하다.

 $e_{ij}={\begin{cases}a_{i},&{\mbox{if }}i\in [1,N]\\b_{ij},&{\mbox{if }}i\in [N+1,2N]\end{cases}}$
 $v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}\delta _{ij}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}$

위 식이 비정규화되었다는 조건과

 $v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}\delta _{ij}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}$

위의 식이 정규화되었다는 조건 하에 아래의 결과가 나온다.

 $\varphi \left(\mathbf {x} \right)=\sum _{i=1}^{2N}\sum _{j=1}^{n}e_{ij}v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big )}$

$\delta _{ij}$은 아래의 식으로 정의된 크론커 델타 함수다.

 $\delta _{ij}={\begin{cases}1,&{\mbox{if }}i=j\\0,&{\mbox{if }}i\neq j\end{cases}}$

참고자료

• Radial basis function network Wikipedia - https://en.wikipedia.org/wiki/Radial_basis_function_network
• Radial Basis Function Network ScienceDirect - https://www.sciencedirect.com/topics/engineering/radial-basis-function-network
• 임시블로그, 〈RBF(Radial Basis Function) 신경망〉, 《티스토리》, 2014-10-27
• jmkang, 〈인공신경망〉, 《인코돔》, 2018-05-09

같이 보기

• 인공신경망
• 다층퍼셉트론

이 방사신경망 문서는 인공지능 기술에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

인공지능 : 인공지능 서비스, 인공지능 로봇, 인공지능 기술 □■⊕, 인공지능 기업, 인공지능 인물 인공지능 기술 AI 워싱 • 로봇공학 • 로봇기술 • 인지과학 • 자동추론 • 자연어 처리 • 지능 • 지식표현 • 컴퓨터 비전 • 튜링 테스트 • 프롬프트 • 프롬프트 엔지니어링 문자인식과 음성인식 ICR • OCR • OMR • TTS • 답변 • 대화 • 문자 • 문자인식 • 스토리 • 음성 • 음성인식(STT) • 인공어 • 자연어 • 질문 • 화자인식 인공지능 데이터 데이터라벨러 • 데이터라벨링 • 데이터셋 • 크라우드워커 • 토큰 • 토큰화 인공지능 학습 ADP • CoLLM • DALL-E • DDPG • DQN • LMM • SARSA • SLM • 강화학습 • 거대언어모델(LLM) • 결정이론적 메타추론 • 계통적 강화학습 • 동적 계획법 • 딥러닝 • 딥큐러닝 • 머신러닝(기계학습) • 모델 기반 강화학습 • 모델 프리 강화학습 • 미세조정 • 반영식 아키텍처 • 비지도학습 • 사전학습 • 수시 알고리즘 • 심층믿음망 • 어니 • 에이전트 • 인공지능 학습 • 지도학습 • 학습 • 확률적 경사하강법 인공지능 알고리즘 AGI • ANI • ASI • RAG • XAI • 관계형 네트워크(RN) • 다층퍼셉트론 • 데이터마이닝 • 방사신경망 • 분산 샌드박스 • 생성대립신경망(GAN) • 생성형 AI • 수퍼얼라인먼트 • 순전파 • 순환신경망(RNN) • 시그모이드 함수 • 신경망 구조 • 심층신경망(DNN) • 심층신뢰신경망(DBN) • 양방향 비고정값 암호 체계(TSID) • 역전파 • 인공신경망(ANN) • 인공지능(AI) • 제한 볼츠만 머신(RBM) • 전방전달신경망 • 코헨 자기조직 신경망 • 텍스트마이닝 • 트랜스포머 • 파이 • 퍼셉트론 • 합성곱 신경망(CNN) 계산복잡도 NP • NP-완전 • 계산복잡도 • 공간복잡도 • 시간복잡도 • 여 NP • 여 NP-완전 인공지능 프로그램 BCI • GPT • 딥블루 • 딥페이크 • 멀티모달 AI • 모달 • 모달리티 • 모달창 • 알렉스넷 • 어니 • 알파고 • 알파고제로 • 알파폴드 • 왓슨 • 카페 • 컨트롤넷 • 텐서플로 • 텔레파시 • 토치 • 파이토치 • 한돌 인공지능 특징 결정이론 • 계산상의 합리성 • 논리학 • 논리주의자 • 분산성 • 불확실성 • 삼단논법 • 선호도 • 예측곤란성 • 완벽한 합리성 • 유계 합리성 • 이유 불충분의 원리 • 자율성 • 최대기대효용 • 할루시네이션 • 효용이론 인공지능 법적 지위 권리주체성 • 소버린 AI • 전자대리인 • 전자적 인간 • 책임법 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반