"효용이론"의 두 판 사이의 차이
(→기대효용이론) |
(→수요곡선의 도출) |
||
| (사용자 2명의 중간 판 41개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''효용이론'''(效用理論, utility theory)은 경제학에서 한 사람이 상품의 소비를 통해 만족(효용)을 얻는다는 개념을 뜻한다. | + | '''효용이론'''(效用理論, utility theory)은 경제학에서 한 사람이 상품의 소비를 통해 만족(효용)을 얻는다는 개념을 뜻한다. 주어진 비용과 시간 단위에 대한 만족의 수준이 높을수록 그 특정 항목을 더욱 원하게 된다. 효용은 기수적 효용과 서수적 효용으로 나눌 수 있다. |
| + | |||
== 개요 == | == 개요 == | ||
| − | + | 효용(效用, utility)이란 특정한 개인이 일정량의 재화를 소비함으로써 얻는 주관적 만족의 정도를 의미한다. 효용은 주관적이므로 소득이 같더라도 사람에 따라 같은 재화에 대한 효용은 달라질 수 있고, 또 같은 개인이더라도 그의 경제 사정에 따라 달라진다. 따라서, 효용에 대한 가측성의 문제와 개인 간 비교 가능성에 대해 날카로운 논쟁이 일어났다. 이에 대해 초기의 효용이론에서는 효용의 심리적인 만족 내지는 욕구를 측정하는 '양'의 개념으로 파악하고, 기수적으로 측정 가능하다고 생각하였다. 이것이 [[기수적 효용]]이다. 예를 들어, 어떤 사람이 사과 한 개의 효용이 10이고 배의 효용이 5라면, 사과의 효용은 배의 그것에 비해 꼭 2배의 만족을 얻고 있다는 것이다. 이에 반해 서수적 효용은 이를 부정하고 단지 재화의 선택에 대한 우선순위만을 알 수 있고, 재의 효용이 타 재의 그것보다 몇 배 큰지 알 수도 없으며 또 알 필요도 없다고 주장한다. 서수적 효용은 각각의 재화에 대해서 소비자에게 동일 만족을 주는 재화의 조합에 초점을 두고 전개된 [[무차별곡선]]의 이론적 배경이 되었다.<ref>기수적효용ㆍ서수적효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=13232&cid=43659&categoryId=43659</ref> | |
| − | + | 효용함수(效用函數, utility function)란 재화 및 용역의 양과 그 효용과의 대응 관계를 말한다. 일정한 종류의 재화나 용역 또는 수종의 재화나 용역의 결합체는 각 개인에 대해서, 일정한 크기의 만족의 정도, 즉 효용을 부여한다. 그러므로 심리적인 만족의 정도를 적당한 척도로 측정하여 이를 <math>U</math>로 하고 <math>X_1, X_2, \cdots, X_n</math>의 소비량을 <math>x_1, x_2, \cdots, x_n</math>이라고 하면, 효용함수는 <math>U = U(x_1, x_2, \cdots, x_n)</math> 라고 쓸 수 있다. 만일 1재화만을 생각한다면, <math>U = F(x_1)</math> 이다. 이것을 그래프로 표시한 경우에 얻어지는 곡선을 [[효용곡선]]이라고 한다. 만일 <math>X_1</math>과 <math>X_2</math>가 서로 독립재이고 한 소비자가 <math>X_1</math>으로부터 50단위, <math>X_2</math>로부터 10단위의 효용을 얻는다면 그 소비자는 60단위의 효용을 얻게 되는데, 이때의 효용을 "기수적 효용" 이라 한다. 따라서 효용함수는 <math>U = U_1(x_1) + U_2(x_2)+ \cdots + U_n(x_n)</math> 라고 쓸 수 있다. 이러한 기수적 효용 학설에 의해 소개된 중요한 경제분석 도구가 바로 [[한계효용]](marginal utility)개념이다. 그러나 위에서 서술한 것처럼 효용을 단위로 측정한다는 것은 불가능한 일로 이 점에 반대해서 서수효용학설이 대두되었다. 즉 효용이란 어떤 단위로 측정될 수 없고 단지 어느 것이 더 큰가 아니면 작은가를 알 수 있을 뿐으로 소비자들은 막연하게나마 느낄 수 있는 더 큰 효용을 선호한다는 것이다. 이러한 서수적 효용은 무차별곡선(indifference curve)을 이용한 소비자 선택이론의 바탕을 이루고 있다. 그러나 기수적 효용이든 서수적 효용이든 소비자의 심리적인 만족의 정도를 측정할 수 있는 특별한 방법이 있다는 가정을 세우고 있어 이 결점을 제거하기 위해 새로운 소비자 선택의 이론이 전개되었다.<ref>효용함수 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=779897&cid=42085&categoryId=42085</ref> | |
| − | + | 총효용(總效用, total utility)은 일정 기간 일정량의 상품을 소비함으로 얻을 수 있는 주관적인 만족의 총량을 뜻한다. 상품의 소비량이 증가하면 일반적으로 총효용도 증가한다. 그러나, 소비량의 증가가 어느 한계점에 도달하면 총효용은 극대가 되고, 그 이상으로 증가하면 총효용은 오히려 감소한다. 예를 들어서 배가 고플 때, 쿠키 한 개를 먹을 때 보다 두 개를 먹을 때 만족감이 높지만, 반복해서 먹다 보면 어느 순간 배가 부르고, 그 이후에는 쿠키를 먹는 것에 만족감을 느끼지 못하고 오히려 불쾌감이 든다.<ref name="한계효용">민윤지, 〈[https://ocw.dongguk.edu/down/2017/201702517407/pdf201702517407.pdf <제6강> 소비자이론(1) : 효용함수와 무차별곡선]〉, 《동국대학교》, 2017-01-25</ref> 여기서 '한계효용'의 개념이 등장한다. 한계효용(限界效用, Marginal utility)이란 어떤 재화나 서비스를 한 단위 더 소비함으로써 얻어지는 총효용의 변화, 즉 개인의 주관적 욕망을 충족시키는 정도를 재는 척도를 의미한다. 이 경우 주관적 만족도는 재화의 단순한 사용가치가 아니라 소비하는 재화의 양의 증감과 연관된 '효용'으로서 받아들여지는데, 주어진 소득 범위 내에 있는 개인의 하나의 재화를 하나의 용도에 1단위 량씩 할당할 때, 주관적 만족이 얻어지는 최후의 1단위(한계단위)의 효용이다.<ref name="철학사전">한계효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=388913&cid=41978&categoryId=41985</ref> | |
== 역사 == | == 역사 == | ||
| − | ; | + | ;기대효용이론 |
| − | 1730년경 스위스의 물리학자 | + | 1730년경 스위스의 물리학자 다니엘 베르누이(Daniel Bernoulli)는, 사람은 화폐에 관해 한계효용이 체감하는 효용함수를 갖고 있으며 도박의 수학적 기대치에서라기보다 도박이 가져오는 효용의 수학적 기대치, 혹은 기대효용을 판단의 기준으로 한다는 가설에 의해 이득의 기대치가 무한대인 도박이라도 실제로는 그 도박에 거금을 내고 참가하는 사람은 없다는 소위 '상트페테르부르크의 역설'을 설명하려고 했다. 1950년대에 들어 폰 노이만(von Neumann)과 모르겐슈테른(Morgenstern) 등이 이 가설에 엄밀한 공리체계(公理體系)로 뒷받침했다. 그 후, 기대효용이론은 게임이론과 밀접히 결부되어 발전하였으며, 경제이론에서도 밀턴 프리드먼(Milton Friedman)과 새비지(Savage)는 기수적 효용에 관한 한계효용체감성이 위험 회피를 의미한다는 것을 명백히 밝히고, 케네스 애로(Kenneth Arrow)와 프래트(Pratt)는 기수적 효용함수의 성질에 입각한 위험회피도의 정의에 성공하는 등, 마르코비츠 이후의 자산 선택이론을 비롯해 불확실성 하에서의 선택 및 경제제도의 일반균형적 분석에 있어서 중심적 역할을 하기에 이르렀다.<ref>기대효용이론 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=1070786&cid=40942&categoryId=31819</ref> |
| − | 1950년대에 들어 | + | |
| + | ;한계효용이론 | ||
| + | 1870년대에 오스트리아의 [[멩거]](Menger), 영국의 [[제본스]](Jevons), 프랑스의 왈라스(Walras)는 한계효용의 법칙을 기초로 해서, 고전파 경제학의 가치론을 비판하고 새로운 경제학설을 주장했다. 이 학파, 특히 멩거를 정점으로 하는 오스트리아 학파는 한계효용학파라고 불리웠다. 멩거는 개인 행위의 심리적 의미를 중시하여 주관가치의 체계로서 경제이론을 구축하고, 제본스는 공리주의 철학의 영향 아래 쾌ㆍ고(快ㆍ苦)의 계산으로부터 출발하여 수학적으로 효용이론을 구축했으며, 왈라스는 콩디약, 튀르고(Turgot) 등의 프롱스 계몽사상의 영향 아래 엄밀한 계산에 의한 균형이론을 구상하는 등 차이는 있으나, 대체로 고전학파의 전통을 계승하여 교환경제사회의 합리성의 기초를 개인의 주관적 가치개념에서 구했다는 점에 특징이 있으며, 근대경제학의 탄생을 고지한 것이었다.<ref name="철학사전"></ref> | ||
| + | |||
| + | == 특성 == | ||
| + | === 불확실성과 합리적 의사결정 === | ||
| + | 불확실성과 합리적 의사결정은 예를 들어, 공항에 도달하기 위한 <math>A_{90}</math> 계획으로 그 계획을 실행했을 때 비행기에 무사히 탑승할 가망이 97%라고 가정하면, 높은 확률은 이 계획이 합리적인 결정임을 뜻하는 것은 아니다. 확률이 더 높은 계획이 있을 수도 있기 때문이다. 비행기를 놓치지 않는 것이 결정적으로 중요하다면, 공항에 더 오래 기다려야 하는 위험을 감수할 수 있다. 탑승 시간보다 하루 전에 집을 떠나는 <math>A_{1440}</math> 계획은 대부분의 경우에도 좋은 선택이 아니다. 제때 비행기를 타게 될 것은 거의 확실하지만, 아주 오래 기다려야 할 가망도 높기 때문이다. 이런 결정을 내릴 때, 에이전트는 반드시 여러 계획의 서로 다른 가능한 결과(outcome)들에 대한 [[선호도]](preference)를 미리 결정해 둘 필요가 있다. 여기서 말하는 결과는 에이전트가 제때 도착했는지, 공항에서 얼마나 기다려야 하는지 같은 요인들이 모두 완결적으로 명시된 하나의 상태를 뜻한다. 선호도를 표현하고 추론할 때에는 효용이론(utility theory)을 사용한다. 여기서 효용은 유용한 정도를 뜻한다. 효용이론에 의하면, 모든 상태에는 그 상태가 에이전트에게 어느 정도나 유용한지 말해 주는 효용이라는 속성이 존재하며, 에이전트는 효용이 높은 상태를 선호한다. 한 상태의 유용은 에이전트에 상대적이다. 예를 들어, 체스에서 백이 흑에게 체크메이트를 한 상태의 효용은 당연히 백 플레이어에게는 높고 흑 플레이어에게는 낮다. | ||
| − | + | 그러나, 체스 경기 규칙에 정해진 <math>1, \frac{1}{2}, 0</math> 같은 점수들을 그대로 효용의 값으로 사용할 수는 없다. 저자들을 포함한 어떤 플레이어는 세계 챔피언 결정전에서 비기는 것을 큰 영광으로 생각하겠지만, 그렇지 않은 플레이어들도 있을 것이기 때문이다. 여기서 취향이나 호불호는 중요하지 않다. 초코칩 아이스크림보다 할라피뇨 풍선껌 아이스크림을 더 좋아하는 에이전트는 좀 괴짜로 느껴지겠지만, 그렇다고 그 에이전트가 비합리적이라고 말할 수는 없다. 효용 함수는 그 어떤 선호도 집합도 감당한다. 효용 함수가 이타주의(altruism)도 감당할 수 있다. 다른 사람들의 안녕을 요인 중 하나로 포함시키면 며, 효용으로 표현된 선호도와 확률론의 조합은 합리적 의사결정에 관한 일반적인 이론인 [[결정이론]](Decision Theory)으로 이어진다. 결정이론은 확률론과 효용이론을 합한 것이다. 결정이론의 근본적인 착안으로, 에이전트는 만일 기대 효용이 가장 높은 동작을 선택한다면 오직 그럴 때만 합리적인 것이다. 여기서 동작의 기대 효용(expected utility)은 그 동작의 모든 가능한 결과 및 효용들의 평균이다. 합리적 에이전트에 대한 이러한 정의를 최대기대효용(MEU) 원리라고 부른다. 기대가 좀 애매모호하고 가설적인 용어로 느껴질 수도 있으나, 여기서 말하는 기댓값인 기대에는 각 결과의 확률을 가중치로 한 결과들의 가중 평균으로 정의된다. 이 원리는 완전히 일반적이다. 또한, 결정이론을 이용해서 동작을 선택하는 에이전트의 구조를 개괄적으로 나타낸 것은 이들이 모두 지금까지의 지각들의 역사가 반영된 믿음 상태를 유지한다는 공통점을 가지고 있다. 주된 차이는, 결정이론에 기초한 에이전트의 믿음 상태는 세계 상태들의 가능 여부(possibility)들만이 아니라 그 상태들의 출현 확률도 나타낸다. 믿음 상태가 주어지면 에이전트는 동작 결과들을 확률적으로 예측할 수 있으며, 기대 효용이 가장 높은 동작을 선택할 수 있다.<ref>스튜어드러셀, 피터노빅, 〈[https://jpub.tistory.com/attachment/cfile8.uf@2549673456B075FB22F910.pdf 인공지능. 2: 현대적 접근방식 제3판]〉, 《제이펍》, 2016-01-29</ref> | |
| − | |||
== 관련 이론 == | == 관련 이론 == | ||
=== 기대효용이론 === | === 기대효용이론 === | ||
| − | + | 기대효용이론(Expected Utility Theory)은 오랜 기간 불확실성 아래에서 경제주체의 의사결정을 분석하는 가장 보편적인 이론으로 사용되어 오고 있다. 기대효용이론은 규범적 이론이다. 규범적 이론은 매우 합리적인 의사결정자가 이론에서 필요한 가정 및 공리를 받아들이고 그에 따라 행동한다면 그 행동의 결과가 어떨지 예측하게 해준다는 장점이 있다. 기대효용이론을 이용하여 불확실성 아래에서의 개인의 선택을 표현한 최초의 성공적인 시도는 von Neumann and Morgenstem(1947)에 의해 이루어졌다고 할 수 있다. 이들은 특정 상황이 발생할 확률 및 그 상황이 발생하는 경우 수취액 또는 지불액을 나타내는 확률변수를 복권으로 정의하고 의사결정자들이 이 복권을 선택한다고 가정하였다. 이들의 가장 중요한 가정 중 하나는 선택자들이 각 상황이 발생할 객관적인 확률을 알고 있다는 것이다. 따라서 선택자들이 객관적 확률 분포를 특정할 수 없는 불확실한 상황에서는 이들의 방법론을 적합한 방법론이라고 하기는 어렵다.<ref name="키리"> 〈[http://www.kiri.or.kr/pdf/%EC%97%B0%EA%B5%AC%EC%9E%90%EB%A3%8C/%EC%97%B0%EA%B5%AC%EB%B3%B4%EA%B3%A0%EC%84%9C/nre2017-22_02.pdf Ⅱ. 불확실성하에서의 선택이론과 유보가격 측정 모형]〉, 《키리보험연구원》</ref> | |
| − | ;''' | + | |
| − | + | ;공리 | |
| − | + | * '''비교 가능성 및 완전성'''(Comparability or Completeness) | |
| − | + | : 불확실한 선택 수단들의 집합 <math>S</math>에 대해 의사결정자는 완전한 선호 순서를 정의할 수 있다. 즉, 집합 <math>S</math>에 속해있는 상이한 선택 수단으로부터의 결과 <math>x</math>와 <math>y</math>에 대해 <math>y</math>보다 <math>x</math>를 선호하거나(<math>x > y</math>), <math>x</math>보다 <math>y</math>를 선호하거나(<math>y > x</math>), <math>x</math>와 <math>y</math>를 동등한 것으로 간주하는(<math>x</math>~<math>y</math>) 것 중 하나의 평가를 할 수 있다. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * '''이행성 및 일관성'''(Transitivity or Consistency) | ||
| + | : 위에서 언급된 선택 결과들의 순서는 완전한 이행성을 가진다. 예를 들어 <math>x</math>가 <math>y</math>보다 선호되고, <math>y</math>가 <math>z</math>보다 선호된다면 <math>x</math>는 <math>z</math>보다 선호된(<math>x > z</math>). 또는 <math>x</math>와 <math>y</math>를 동등하게 여기고, <math>y</math>와 <math>z</math>도 동등하게 여긴다면, <math>x</math>와 <math>z</math>도 동등하게 여긴다. | ||
| + | * '''강한 독립성'''(Strong Independence) | ||
| + | : <math>x</math>가 나타날 확률이 <math>a</math>, <math>z</math>가 나타날 확률이 <math>1 - a</math>인 게임을 <math>G(x, z:a)</math>로 표현하자. 이와 유사하게 <math>y</math>가 나타날 확률이 <math>a</math>, <math>z</math>가 나타날 확률이 <math>1 - a</math>인 게임을 <math>G(y, z:a)</math>로 표현하자. 만일 <math>x</math>와 <math>y</math>를 동등하게 여긴다면, 이 개인은 <math>G(x, z:a)</math>와 <math>G(y, z:a)</math>를 동등한 것으로 여긴다. 또한 <math>x</math>를 <math>y</math> 보다 선호한다면 <math>G(x, z:a)</math>를 <math>G(y, z:a)</math>보다 선호하고, <math>y</math>를 <math>x</math> 보다 선호한다면 <math>G(y, z:a)</math>를 <math>G(x, z:a)</math> 보다 선호한다. | ||
| + | * '''측정 가능성'''(Measurability) | ||
| + | : <math>x >= y</math>를 '<math>x</math>를 <math>y</math> 보다 선호하거나 최소한 동등하게 간주한다'는 표현이라고 하자. 만일 선택 결과 <math>x, y, z</math>가 <math>x >= y >= z</math>또는 <math>x >= y > z</math>를 만족한다면, <math>y</math>~<math>G(x, z:a)</math>인 유일한 확률 <math>a</math>가 존재한다. | ||
| − | + | * '''순위'''(Ranking) | |
| − | + | : <math>x >= y >= z</math>이고, <math>x >= u >= z</math>라고 가정하자. 이때 만일 <math>y</math>~<math>G(x, z:a_1)</math>이고 <math>u</math>~<math>G(x, z:a_2)</math>이면 <math>a_1 > a_2</math>는 <math>y > u</math>를 의미하고 <math>a_1 = a_2</math> 는 <math>y</math>~<math>u</math>를 의미한다. | |
| − | |||
| − | + | 확실성 하의 선택이라면 비교 가능성 및 완전성과 이행성 및 일관성으로 충분하다. 그러나, 의사결정자의 신호를 기대효용이론에서 구현하기 위해서는 강한 독립성부터 순위까지 추가적인 공리들이 필요하다. 강한 독립성 원칙은 기대효용이론에서 이 공리의 중요성은 직관적으로도 어렵지 않게 이해할 수 있다. 기대효용 규칙이 적용 가능하다면, 특정한 의사결정의 효용은 그 결정으로부터 발생하는 각 결과의 효용의 가중 합계가 된다. 각 결과의 가중치가 같은 경우, 이러한 결과들이 다양한 방법으로 조합되어도 상호 배타적인 특정 결과에 대한 의사결정자의 태도는 영향을 받지 않는다. 이는 강한 독립성의 직접적인 가정이다. 이 독립성 공리가 합리적으로 인간의 행동을 묘사하는지에 대해서는 많은 논란이 있다. 예를 들어 <math>x</math>와 <math>y</math>가 개인이 동등하게 여기는 두 가지 상품이라고 하자. 이때 임의의 제3의 상품 <math>z</math>에 대해 개인은 <math>a</math>의 확률로 <math>x</math>를 얻거나 <math>1-a</math>의 확률로 <math>z</math>를 얻는 게임, <math>a</math>의 확률로 <math>y</math>를 얻거나 <math>1-a</math>의 확률로 <math>z</math>를 얻는 게임을 동등하게 여긴다는 것이 이 공리의 핵심이다. <math>z</math>가 <math>x</math>와 결합한 결과와 <math>z</math>가 <math>y</math>와 결합한 결과의 만족도가 같을 때 이 공리는 합리적이라고 할 것이다. 그러나 <math>x</math>와 <math>y</math>가 <math>z</math>와 결합한 결과가 다른 만족도를 줄 때는 이 공리는 합리적인 것으로 간주하기 어렵게 된다. 기대효용이론에서 도출된 도용함수 <math>U</math>는 두 가지 특성을 보인다. 첫째, 결과에 대한 선호는 효용함수로 계산된 효용의 크기로 나타나며 그 순위가 유지되어야 한다. 즉, 개인이 <math>x</math>를 <math>y</math> 보다 선호하면 <math>U(x) > U(y)</math>이다. 둘째, 기대효용을 이용하면 불확실성 아래에서의 선택 수단들에 대한 순위를 정할 수 있다. <math>x</math>를 택하는 경우 발생 확률 <math>p_i</math>인 상황 <math>i</math>에 따라, <math>x_i</math>가 나타나며 발생 가능한 전체 상황의 수가 <math>n</math>개라면 <math>x</math>의 기대효용은 수학적으로 다음과 같다. | |
| − | |||
| − | |||
| − | < | + | '''x의 기대효용 :''' <math>E[U(x)] = \sum_{i=1}^n p_iU(x_i)</math> |
| + | 또한 <math>y</math>를 택하는 경우 발생 확률 <math>q_j</math>인 상황 <math>j</math>에 따라 <math>y_j</math>가 나타나며 발생 가능한 전체 상황의 수가 <math>m</math>개라면 <math>y</math>의 기대효용은 수학적으로 다음과 같다. | ||
| − | + | '''y의 기대효용 :''' <math>E[U(y)] = \sum_{j=1}^m q_jU(y_j)</math> | |
| − | + | 기대효용이론은 <math>E[U(x)] > E[U(y)]</math>이면 사람들은 <math>y</math>보다 <math>x</math>를 선호한다는 것을 의미한다. 일반적으로 <math>x_i</math> 및 <math>y_j</math>는 상황 <math>i</math> 및 상황 <math>j</math>에서의 총재산 또는 총소비이며, <math>p_i</math>와 <math>q_j</math>는 각각 상황 <math>i</math>와 상황 <math>j</math>가 발생할 객관적 확률이 사용된다.<ref name="키리"></ref> | |
| − | + | ||
| − | 기대효용이론은 | + | === 한계 효용이론 === |
| + | <math>MUx = \frac{\Delta TU}{\Delta X}</math>, <math>MUy = \frac{\Delta TU}{\Delta Y}</math> | ||
| + | |||
| + | 한계효용(MU)은 재화 1단위를 추가로 소비했을 때 총효용의 증가분을 말한다. 즉, 소비량 1단위가 증가할 때 변화하는 총효용의 증가분, 소비량 1단위가 감소할 때 변화하는 총효용의 감소분과 같은 총효용의 변화분(∆U)을 소비량의 변화분(∆X)으로 나눈 값이다.<ref name="한계효용"></ref> | ||
| + | |||
| + | ==== 한계 효용체감의 법칙 ==== | ||
| + | [[파일:한계효용체감의 법칙.jpg|썸네일|400픽셀|'''한계효용체감의 법칙''']] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
허만 고센(Hermann Heinrich Gossen)이 주장한 고센의 제1법칙, 한계효용체감의 법칙은 재화의 소비가 증가함에 따라 처음에는 한계효용이 증가하지만, 어느 단계를 지나면 감소하는 현상이 일어난다는 것이다. 이 현상에도 예외가 있는데, '술'과 '돈' 같은 경우에는 더 많이 소비할수록 효용이 증가하기도 한다.<ref name="한효이">젊은미소, 〈[http://blog.daum.net/orion3727/2802 제 11 장. 한계효용이론]〉, 《다음 블로그》, 2013-09-27</ref> | 허만 고센(Hermann Heinrich Gossen)이 주장한 고센의 제1법칙, 한계효용체감의 법칙은 재화의 소비가 증가함에 따라 처음에는 한계효용이 증가하지만, 어느 단계를 지나면 감소하는 현상이 일어난다는 것이다. 이 현상에도 예외가 있는데, '술'과 '돈' 같은 경우에는 더 많이 소비할수록 효용이 증가하기도 한다.<ref name="한효이">젊은미소, 〈[http://blog.daum.net/orion3727/2802 제 11 장. 한계효용이론]〉, 《다음 블로그》, 2013-09-27</ref> | ||
| − | |||
| − | |||
| − | + | ==== 수요곡선의 도출 ==== | |
| + | [[파일:한계효용이론 수요곡선.jpg|썸네일|400픽셀|'''한계효용 이론에 따른 수요곡선의 도출''']] | ||
| + | |||
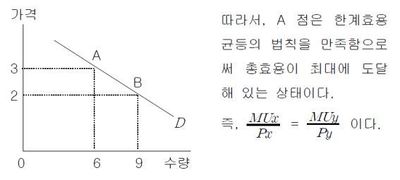
| + | 우측 그림은 <math>P_x</math> = 3원, <math>P_y</math> = 2원, <math>Q_x</math> = 6단위, <math>Q_y</math> = 9단위, <math>I</math> = 26원'이라는 조건을 줬을 때 그래프로 나타낸 것이다. 다른 조건들이 일정한 상태에서 <math>X</math>재의 가격만 3원에서 2원으로 하락하면, 한계효용 균등의 균형이 깨지게 된다. 즉, <math>X</math>재의 단위가격당 한계효용이 <math>Y</math>재의 단위가격당 한계효용보다 크게 된다. 이에 총효용 극대를 위해서 소비자는 <math>Y</math>재의 소비를 줄이고 <math>X</math>재의 소비를 늘리는 조정을 하게 된다. 결국, 이러한 조정은 한계효용체감의 법칙에 따라 <math>X</math>재의 한계효용이 다시 감소하여 다시 <math>X</math>재의 단위가격당 한계효용과 <math>Y</math>재의 단위가격당 한계효용이 같아진다. 그 결과 새로운 균형점 <math>B</math> 점이 형성된다.<ref name="한효이"></ref> | ||
| + | |||
소비자는 주어진 소득으로 최대의 효용을 얻기 위해 합리적인 소비를 하려고 한다. 따라서 몇 종류의 재화나 서비스를 동시에 소비할 때 각 재화나 서비스가 가진 한계효용이 같지 않다면 한계효용이 낮은 재화를 소비하는 대신 한계효용이 높은 다른 재화를 소비하여 전체의 효용을 크게 할 것이다. 이때 각 재화의 1원어치의 한계효용이 모두 같아질 때 소비자가 느끼는 총효용은 극대화된다. 이처럼 모든 재화의 1원어치의 한계효용이 균등하게 되어 각 재화를 소비하는 양을 변화시킬 필요가 없는 경우를 ‘한계효용이 균등하다’라고 표현하고, 이를 ‘한계효용균등의 법칙’이라고 한다. 우측 그림은 효용 극대화가 충족된 상태이다.<ref>〈[http://www.sisanews.kr/news/articleView.html?idxno=4679 한계효용 균등의 법칙]〉, 《시사경제신문》, 2015-03-05</ref> | 소비자는 주어진 소득으로 최대의 효용을 얻기 위해 합리적인 소비를 하려고 한다. 따라서 몇 종류의 재화나 서비스를 동시에 소비할 때 각 재화나 서비스가 가진 한계효용이 같지 않다면 한계효용이 낮은 재화를 소비하는 대신 한계효용이 높은 다른 재화를 소비하여 전체의 효용을 크게 할 것이다. 이때 각 재화의 1원어치의 한계효용이 모두 같아질 때 소비자가 느끼는 총효용은 극대화된다. 이처럼 모든 재화의 1원어치의 한계효용이 균등하게 되어 각 재화를 소비하는 양을 변화시킬 필요가 없는 경우를 ‘한계효용이 균등하다’라고 표현하고, 이를 ‘한계효용균등의 법칙’이라고 한다. 우측 그림은 효용 극대화가 충족된 상태이다.<ref>〈[http://www.sisanews.kr/news/articleView.html?idxno=4679 한계효용 균등의 법칙]〉, 《시사경제신문》, 2015-03-05</ref> | ||
| − | + | ==== 경제학 관점 ==== | |
| − | + | 오스트리아학파는 주류 경제학과 달리 심리학적 가정들을 이용하지 않고 순수 논리만으로 한계 효용 체감의 법칙을 논증한다. 예컨대 재화 <math>X</math> 5단위를 가지고 있는 한 사람을 예를들면, 이 사람은 이 재화 <math>X</math>의 첫 번째 단위를 그 재화 <math>X</math>가 봉사할 수 있는 목적 중에서 가장 시급하고 가장 높은 가치를 갖는 목적들에 먼저 사용할 것이다. 그렇게 된다면 당연히 재화 <math>X</math>의 두 번째 단위는 그보다 덜 시급하고 덜 높은 가치를 갖는 목적들에 사용될 것이고, 세 번째, 네 번째, 다섯 번째 단위로 갈수록 점점 더 낮은 효용을 충족시키는 데 사용될 것이다. 그렇다면 마지막 단위가 가장 낮은 효용을 충족시키는 데 사용될 것이 명백한데, 이 단위를 바로 한계 단위(marginal unit)이라고 하고 이 한계 단위에 의해 제공되는 만족, 즉 이 한계 단위가 충족시키는 효용이 바로 한계 효용인 것이다. 그렇다면 이제 이 재화 <math>X</math>가 더 많이 공급될수록, 즉 여섯 번째, 일곱 번째, 여덟 번째 단위가 추가될수록 한계 단위에 의해 제공되는 만족인 한계 효용은 당연히 논리적으로 하락할 수밖에 없다. 왜냐하면, 원래 다섯 번째 단위까지밖에 없었던 재화 <math>X</math>가 세 단위 더 추가된다면, 이 경우에는 당연히 한계 단위인 여덟 번째 단위는 다섯번째 단위보다 덜 가치 있고 더 낮은 효용을 충족시키는 데 사용될 것이기 때문에이다. | |
| + | |||
| + | 한계 단위에 의해 제공되는 만족인 한계 효용은 하락하기 때문이다. 예를 들어 물 5병을 가지고 있는 사람이 있다면, 이 사람은 물 1병을 현재로서 가장 시급하고 가장 높은 가치를 가지는 목적을 충족시키는 데 먼저 사용할 것이다. 즉, 지금 몹시 목이 마르다면 먼저 물을 마시는데 사용할 것이다. 그렇다면 이제 그는 또 다른 물 1병을 그것보다 조금은 덜 시급하고 낮은 가치를 가지는 목적을 충족시키는데 사용할 것이다. 예를 들면, 세수 하거나 씻는 데 사용할 것이다. 마지막 단위인 물 1병은 그는 가장 낮은 효용을 충족시키는 데, 예를 들면 화초에 물을 주는 데 사용할 것이다. 이 경우, 한계 효용은 화초에 물을 줌으로써 얻는 효용이다. 만약 같은 조건에서 물 한 병을 가지고 있다면 이 경우 한계 효용은 물을 마심으로써 얻는 효용이다. 따라서 어떤 재화의 단위 공급이 증가할수록, 그 재화의 가장 마지막 단위로부터 얻어지는 효용인 한계 효용은 더 감소할 수밖에 없다. 행위자의 가치 척도에서 필연적으로 더 낮은 순위의 목적에 봉사하는 데 사용될 것이기 때문이다. 한계효용균등의 법칙은 다음과 같다.<ref>한계효용체감의 법칙 나무위키 - https://namu.wiki/w/%ED%95%9C%EA%B3%84%20%ED%9A%A8%EC%9A%A9%20%EC%B2%B4%EA%B0%90%EC%9D%98%20%EB%B2%95%EC%B9%99?from=%ED%95%9C%EA%B3%84%ED%9A%A8%EC%9A%A9%EC%B2%B4%EA%B0%90%EC%9D%98%20%EB%B2%95%EC%B9%99</ref> | ||
| + | |||
| + | <math>\frac{MU_1}{P_!} = \frac{MU_2}{P_2} = \frac{MU_3}{P_3} = \cdots\cdots = \frac{MU_n}{P_n} = m</math> (m: 화폐 한 단위의 한계효용) | ||
{{각주}} | {{각주}} | ||
| 76번째 줄: | 85번째 줄: | ||
* 기수적효용ㆍ서수적효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=13232&cid=43659&categoryId=43659 | * 기수적효용ㆍ서수적효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=13232&cid=43659&categoryId=43659 | ||
* 크네이트, 〈[https://m.blog.naver.com/PostView.nhn?blogId=2035icck&logNo=220838010688&proxyReferer=https:%2F%2Fwww.google.com%2F 기대효용 이론(expected utility theory)]〉, 《네이버 블로그》, 2016-10-17 | * 크네이트, 〈[https://m.blog.naver.com/PostView.nhn?blogId=2035icck&logNo=220838010688&proxyReferer=https:%2F%2Fwww.google.com%2F 기대효용 이론(expected utility theory)]〉, 《네이버 블로그》, 2016-10-17 | ||
| + | * 스튜어드러셀, 피터노빅, 〈[https://jpub.tistory.com/attachment/cfile8.uf@2549673456B075FB22F910.pdf 인공지능. 2: 현대적 접근방식 제3판]〉, 《제이펍》, 2016-01-29 | ||
== 같이 보기 == | == 같이 보기 == | ||
2023년 6월 24일 (토) 14:08 기준 최신판
효용이론(效用理論, utility theory)은 경제학에서 한 사람이 상품의 소비를 통해 만족(효용)을 얻는다는 개념을 뜻한다. 주어진 비용과 시간 단위에 대한 만족의 수준이 높을수록 그 특정 항목을 더욱 원하게 된다. 효용은 기수적 효용과 서수적 효용으로 나눌 수 있다.
목차
개요[편집]
효용(效用, utility)이란 특정한 개인이 일정량의 재화를 소비함으로써 얻는 주관적 만족의 정도를 의미한다. 효용은 주관적이므로 소득이 같더라도 사람에 따라 같은 재화에 대한 효용은 달라질 수 있고, 또 같은 개인이더라도 그의 경제 사정에 따라 달라진다. 따라서, 효용에 대한 가측성의 문제와 개인 간 비교 가능성에 대해 날카로운 논쟁이 일어났다. 이에 대해 초기의 효용이론에서는 효용의 심리적인 만족 내지는 욕구를 측정하는 '양'의 개념으로 파악하고, 기수적으로 측정 가능하다고 생각하였다. 이것이 기수적 효용이다. 예를 들어, 어떤 사람이 사과 한 개의 효용이 10이고 배의 효용이 5라면, 사과의 효용은 배의 그것에 비해 꼭 2배의 만족을 얻고 있다는 것이다. 이에 반해 서수적 효용은 이를 부정하고 단지 재화의 선택에 대한 우선순위만을 알 수 있고, 재의 효용이 타 재의 그것보다 몇 배 큰지 알 수도 없으며 또 알 필요도 없다고 주장한다. 서수적 효용은 각각의 재화에 대해서 소비자에게 동일 만족을 주는 재화의 조합에 초점을 두고 전개된 무차별곡선의 이론적 배경이 되었다.[1]
효용함수(效用函數, utility function)란 재화 및 용역의 양과 그 효용과의 대응 관계를 말한다. 일정한 종류의 재화나 용역 또는 수종의 재화나 용역의 결합체는 각 개인에 대해서, 일정한 크기의 만족의 정도, 즉 효용을 부여한다. 그러므로 심리적인 만족의 정도를 적당한 척도로 측정하여 이를 로 하고 의 소비량을 이라고 하면, 효용함수는 라고 쓸 수 있다. 만일 1재화만을 생각한다면, 이다. 이것을 그래프로 표시한 경우에 얻어지는 곡선을 효용곡선이라고 한다. 만일 과 가 서로 독립재이고 한 소비자가 으로부터 50단위, 로부터 10단위의 효용을 얻는다면 그 소비자는 60단위의 효용을 얻게 되는데, 이때의 효용을 "기수적 효용" 이라 한다. 따라서 효용함수는 라고 쓸 수 있다. 이러한 기수적 효용 학설에 의해 소개된 중요한 경제분석 도구가 바로 한계효용(marginal utility)개념이다. 그러나 위에서 서술한 것처럼 효용을 단위로 측정한다는 것은 불가능한 일로 이 점에 반대해서 서수효용학설이 대두되었다. 즉 효용이란 어떤 단위로 측정될 수 없고 단지 어느 것이 더 큰가 아니면 작은가를 알 수 있을 뿐으로 소비자들은 막연하게나마 느낄 수 있는 더 큰 효용을 선호한다는 것이다. 이러한 서수적 효용은 무차별곡선(indifference curve)을 이용한 소비자 선택이론의 바탕을 이루고 있다. 그러나 기수적 효용이든 서수적 효용이든 소비자의 심리적인 만족의 정도를 측정할 수 있는 특별한 방법이 있다는 가정을 세우고 있어 이 결점을 제거하기 위해 새로운 소비자 선택의 이론이 전개되었다.[2]
총효용(總效用, total utility)은 일정 기간 일정량의 상품을 소비함으로 얻을 수 있는 주관적인 만족의 총량을 뜻한다. 상품의 소비량이 증가하면 일반적으로 총효용도 증가한다. 그러나, 소비량의 증가가 어느 한계점에 도달하면 총효용은 극대가 되고, 그 이상으로 증가하면 총효용은 오히려 감소한다. 예를 들어서 배가 고플 때, 쿠키 한 개를 먹을 때 보다 두 개를 먹을 때 만족감이 높지만, 반복해서 먹다 보면 어느 순간 배가 부르고, 그 이후에는 쿠키를 먹는 것에 만족감을 느끼지 못하고 오히려 불쾌감이 든다.[3] 여기서 '한계효용'의 개념이 등장한다. 한계효용(限界效用, Marginal utility)이란 어떤 재화나 서비스를 한 단위 더 소비함으로써 얻어지는 총효용의 변화, 즉 개인의 주관적 욕망을 충족시키는 정도를 재는 척도를 의미한다. 이 경우 주관적 만족도는 재화의 단순한 사용가치가 아니라 소비하는 재화의 양의 증감과 연관된 '효용'으로서 받아들여지는데, 주어진 소득 범위 내에 있는 개인의 하나의 재화를 하나의 용도에 1단위 량씩 할당할 때, 주관적 만족이 얻어지는 최후의 1단위(한계단위)의 효용이다.[4]
역사[편집]
- 기대효용이론
1730년경 스위스의 물리학자 다니엘 베르누이(Daniel Bernoulli)는, 사람은 화폐에 관해 한계효용이 체감하는 효용함수를 갖고 있으며 도박의 수학적 기대치에서라기보다 도박이 가져오는 효용의 수학적 기대치, 혹은 기대효용을 판단의 기준으로 한다는 가설에 의해 이득의 기대치가 무한대인 도박이라도 실제로는 그 도박에 거금을 내고 참가하는 사람은 없다는 소위 '상트페테르부르크의 역설'을 설명하려고 했다. 1950년대에 들어 폰 노이만(von Neumann)과 모르겐슈테른(Morgenstern) 등이 이 가설에 엄밀한 공리체계(公理體系)로 뒷받침했다. 그 후, 기대효용이론은 게임이론과 밀접히 결부되어 발전하였으며, 경제이론에서도 밀턴 프리드먼(Milton Friedman)과 새비지(Savage)는 기수적 효용에 관한 한계효용체감성이 위험 회피를 의미한다는 것을 명백히 밝히고, 케네스 애로(Kenneth Arrow)와 프래트(Pratt)는 기수적 효용함수의 성질에 입각한 위험회피도의 정의에 성공하는 등, 마르코비츠 이후의 자산 선택이론을 비롯해 불확실성 하에서의 선택 및 경제제도의 일반균형적 분석에 있어서 중심적 역할을 하기에 이르렀다.[5]
- 한계효용이론
1870년대에 오스트리아의 멩거(Menger), 영국의 제본스(Jevons), 프랑스의 왈라스(Walras)는 한계효용의 법칙을 기초로 해서, 고전파 경제학의 가치론을 비판하고 새로운 경제학설을 주장했다. 이 학파, 특히 멩거를 정점으로 하는 오스트리아 학파는 한계효용학파라고 불리웠다. 멩거는 개인 행위의 심리적 의미를 중시하여 주관가치의 체계로서 경제이론을 구축하고, 제본스는 공리주의 철학의 영향 아래 쾌ㆍ고(快ㆍ苦)의 계산으로부터 출발하여 수학적으로 효용이론을 구축했으며, 왈라스는 콩디약, 튀르고(Turgot) 등의 프롱스 계몽사상의 영향 아래 엄밀한 계산에 의한 균형이론을 구상하는 등 차이는 있으나, 대체로 고전학파의 전통을 계승하여 교환경제사회의 합리성의 기초를 개인의 주관적 가치개념에서 구했다는 점에 특징이 있으며, 근대경제학의 탄생을 고지한 것이었다.[4]
특성[편집]
불확실성과 합리적 의사결정[편집]
불확실성과 합리적 의사결정은 예를 들어, 공항에 도달하기 위한 계획으로 그 계획을 실행했을 때 비행기에 무사히 탑승할 가망이 97%라고 가정하면, 높은 확률은 이 계획이 합리적인 결정임을 뜻하는 것은 아니다. 확률이 더 높은 계획이 있을 수도 있기 때문이다. 비행기를 놓치지 않는 것이 결정적으로 중요하다면, 공항에 더 오래 기다려야 하는 위험을 감수할 수 있다. 탑승 시간보다 하루 전에 집을 떠나는 계획은 대부분의 경우에도 좋은 선택이 아니다. 제때 비행기를 타게 될 것은 거의 확실하지만, 아주 오래 기다려야 할 가망도 높기 때문이다. 이런 결정을 내릴 때, 에이전트는 반드시 여러 계획의 서로 다른 가능한 결과(outcome)들에 대한 선호도(preference)를 미리 결정해 둘 필요가 있다. 여기서 말하는 결과는 에이전트가 제때 도착했는지, 공항에서 얼마나 기다려야 하는지 같은 요인들이 모두 완결적으로 명시된 하나의 상태를 뜻한다. 선호도를 표현하고 추론할 때에는 효용이론(utility theory)을 사용한다. 여기서 효용은 유용한 정도를 뜻한다. 효용이론에 의하면, 모든 상태에는 그 상태가 에이전트에게 어느 정도나 유용한지 말해 주는 효용이라는 속성이 존재하며, 에이전트는 효용이 높은 상태를 선호한다. 한 상태의 유용은 에이전트에 상대적이다. 예를 들어, 체스에서 백이 흑에게 체크메이트를 한 상태의 효용은 당연히 백 플레이어에게는 높고 흑 플레이어에게는 낮다.
그러나, 체스 경기 규칙에 정해진 같은 점수들을 그대로 효용의 값으로 사용할 수는 없다. 저자들을 포함한 어떤 플레이어는 세계 챔피언 결정전에서 비기는 것을 큰 영광으로 생각하겠지만, 그렇지 않은 플레이어들도 있을 것이기 때문이다. 여기서 취향이나 호불호는 중요하지 않다. 초코칩 아이스크림보다 할라피뇨 풍선껌 아이스크림을 더 좋아하는 에이전트는 좀 괴짜로 느껴지겠지만, 그렇다고 그 에이전트가 비합리적이라고 말할 수는 없다. 효용 함수는 그 어떤 선호도 집합도 감당한다. 효용 함수가 이타주의(altruism)도 감당할 수 있다. 다른 사람들의 안녕을 요인 중 하나로 포함시키면 며, 효용으로 표현된 선호도와 확률론의 조합은 합리적 의사결정에 관한 일반적인 이론인 결정이론(Decision Theory)으로 이어진다. 결정이론은 확률론과 효용이론을 합한 것이다. 결정이론의 근본적인 착안으로, 에이전트는 만일 기대 효용이 가장 높은 동작을 선택한다면 오직 그럴 때만 합리적인 것이다. 여기서 동작의 기대 효용(expected utility)은 그 동작의 모든 가능한 결과 및 효용들의 평균이다. 합리적 에이전트에 대한 이러한 정의를 최대기대효용(MEU) 원리라고 부른다. 기대가 좀 애매모호하고 가설적인 용어로 느껴질 수도 있으나, 여기서 말하는 기댓값인 기대에는 각 결과의 확률을 가중치로 한 결과들의 가중 평균으로 정의된다. 이 원리는 완전히 일반적이다. 또한, 결정이론을 이용해서 동작을 선택하는 에이전트의 구조를 개괄적으로 나타낸 것은 이들이 모두 지금까지의 지각들의 역사가 반영된 믿음 상태를 유지한다는 공통점을 가지고 있다. 주된 차이는, 결정이론에 기초한 에이전트의 믿음 상태는 세계 상태들의 가능 여부(possibility)들만이 아니라 그 상태들의 출현 확률도 나타낸다. 믿음 상태가 주어지면 에이전트는 동작 결과들을 확률적으로 예측할 수 있으며, 기대 효용이 가장 높은 동작을 선택할 수 있다.[6]
관련 이론[편집]
기대효용이론[편집]
기대효용이론(Expected Utility Theory)은 오랜 기간 불확실성 아래에서 경제주체의 의사결정을 분석하는 가장 보편적인 이론으로 사용되어 오고 있다. 기대효용이론은 규범적 이론이다. 규범적 이론은 매우 합리적인 의사결정자가 이론에서 필요한 가정 및 공리를 받아들이고 그에 따라 행동한다면 그 행동의 결과가 어떨지 예측하게 해준다는 장점이 있다. 기대효용이론을 이용하여 불확실성 아래에서의 개인의 선택을 표현한 최초의 성공적인 시도는 von Neumann and Morgenstem(1947)에 의해 이루어졌다고 할 수 있다. 이들은 특정 상황이 발생할 확률 및 그 상황이 발생하는 경우 수취액 또는 지불액을 나타내는 확률변수를 복권으로 정의하고 의사결정자들이 이 복권을 선택한다고 가정하였다. 이들의 가장 중요한 가정 중 하나는 선택자들이 각 상황이 발생할 객관적인 확률을 알고 있다는 것이다. 따라서 선택자들이 객관적 확률 분포를 특정할 수 없는 불확실한 상황에서는 이들의 방법론을 적합한 방법론이라고 하기는 어렵다.[7]
- 공리
- 비교 가능성 및 완전성(Comparability or Completeness)
- 불확실한 선택 수단들의 집합 에 대해 의사결정자는 완전한 선호 순서를 정의할 수 있다. 즉, 집합 에 속해있는 상이한 선택 수단으로부터의 결과 와 에 대해 보다 를 선호하거나(), 보다 를 선호하거나(), 와 를 동등한 것으로 간주하는(~) 것 중 하나의 평가를 할 수 있다.
- 이행성 및 일관성(Transitivity or Consistency)
- 위에서 언급된 선택 결과들의 순서는 완전한 이행성을 가진다. 예를 들어 가 보다 선호되고, 가 보다 선호된다면 는 보다 선호된(). 또는 와 를 동등하게 여기고, 와 도 동등하게 여긴다면, 와 도 동등하게 여긴다.
- 강한 독립성(Strong Independence)
- 가 나타날 확률이 , 가 나타날 확률이 인 게임을 로 표현하자. 이와 유사하게 가 나타날 확률이 , 가 나타날 확률이 인 게임을 로 표현하자. 만일 와 를 동등하게 여긴다면, 이 개인은 와 를 동등한 것으로 여긴다. 또한 를 보다 선호한다면 를 보다 선호하고, 를 보다 선호한다면 를 보다 선호한다.
- 측정 가능성(Measurability)
- 를 '를 보다 선호하거나 최소한 동등하게 간주한다'는 표현이라고 하자. 만일 선택 결과 가 또는 를 만족한다면, ~인 유일한 확률 가 존재한다.
- 순위(Ranking)
- 이고, 라고 가정하자. 이때 만일 ~이고 ~이면 는 를 의미하고 는 ~를 의미한다.
확실성 하의 선택이라면 비교 가능성 및 완전성과 이행성 및 일관성으로 충분하다. 그러나, 의사결정자의 신호를 기대효용이론에서 구현하기 위해서는 강한 독립성부터 순위까지 추가적인 공리들이 필요하다. 강한 독립성 원칙은 기대효용이론에서 이 공리의 중요성은 직관적으로도 어렵지 않게 이해할 수 있다. 기대효용 규칙이 적용 가능하다면, 특정한 의사결정의 효용은 그 결정으로부터 발생하는 각 결과의 효용의 가중 합계가 된다. 각 결과의 가중치가 같은 경우, 이러한 결과들이 다양한 방법으로 조합되어도 상호 배타적인 특정 결과에 대한 의사결정자의 태도는 영향을 받지 않는다. 이는 강한 독립성의 직접적인 가정이다. 이 독립성 공리가 합리적으로 인간의 행동을 묘사하는지에 대해서는 많은 논란이 있다. 예를 들어 와 가 개인이 동등하게 여기는 두 가지 상품이라고 하자. 이때 임의의 제3의 상품 에 대해 개인은 의 확률로 를 얻거나 의 확률로 를 얻는 게임, 의 확률로 를 얻거나 의 확률로 를 얻는 게임을 동등하게 여긴다는 것이 이 공리의 핵심이다. 가 와 결합한 결과와 가 와 결합한 결과의 만족도가 같을 때 이 공리는 합리적이라고 할 것이다. 그러나 와 가 와 결합한 결과가 다른 만족도를 줄 때는 이 공리는 합리적인 것으로 간주하기 어렵게 된다. 기대효용이론에서 도출된 도용함수 는 두 가지 특성을 보인다. 첫째, 결과에 대한 선호는 효용함수로 계산된 효용의 크기로 나타나며 그 순위가 유지되어야 한다. 즉, 개인이 를 보다 선호하면 이다. 둘째, 기대효용을 이용하면 불확실성 아래에서의 선택 수단들에 대한 순위를 정할 수 있다. 를 택하는 경우 발생 확률 인 상황 에 따라, 가 나타나며 발생 가능한 전체 상황의 수가 개라면 의 기대효용은 수학적으로 다음과 같다.
x의 기대효용 :
또한 를 택하는 경우 발생 확률 인 상황 에 따라 가 나타나며 발생 가능한 전체 상황의 수가 개라면 의 기대효용은 수학적으로 다음과 같다.
y의 기대효용 :
기대효용이론은 이면 사람들은 보다 를 선호한다는 것을 의미한다. 일반적으로 및 는 상황 및 상황 에서의 총재산 또는 총소비이며, 와 는 각각 상황 와 상황 가 발생할 객관적 확률이 사용된다.[7]
한계 효용이론[편집]
,
한계효용(MU)은 재화 1단위를 추가로 소비했을 때 총효용의 증가분을 말한다. 즉, 소비량 1단위가 증가할 때 변화하는 총효용의 증가분, 소비량 1단위가 감소할 때 변화하는 총효용의 감소분과 같은 총효용의 변화분(∆U)을 소비량의 변화분(∆X)으로 나눈 값이다.[3]
한계 효용체감의 법칙[편집]
허만 고센(Hermann Heinrich Gossen)이 주장한 고센의 제1법칙, 한계효용체감의 법칙은 재화의 소비가 증가함에 따라 처음에는 한계효용이 증가하지만, 어느 단계를 지나면 감소하는 현상이 일어난다는 것이다. 이 현상에도 예외가 있는데, '술'과 '돈' 같은 경우에는 더 많이 소비할수록 효용이 증가하기도 한다.[8]
수요곡선의 도출[편집]
우측 그림은 = 3원, = 2원, = 6단위, = 9단위, = 26원'이라는 조건을 줬을 때 그래프로 나타낸 것이다. 다른 조건들이 일정한 상태에서 재의 가격만 3원에서 2원으로 하락하면, 한계효용 균등의 균형이 깨지게 된다. 즉, 재의 단위가격당 한계효용이 재의 단위가격당 한계효용보다 크게 된다. 이에 총효용 극대를 위해서 소비자는 재의 소비를 줄이고 재의 소비를 늘리는 조정을 하게 된다. 결국, 이러한 조정은 한계효용체감의 법칙에 따라 재의 한계효용이 다시 감소하여 다시 재의 단위가격당 한계효용과 재의 단위가격당 한계효용이 같아진다. 그 결과 새로운 균형점 점이 형성된다.[8]
소비자는 주어진 소득으로 최대의 효용을 얻기 위해 합리적인 소비를 하려고 한다. 따라서 몇 종류의 재화나 서비스를 동시에 소비할 때 각 재화나 서비스가 가진 한계효용이 같지 않다면 한계효용이 낮은 재화를 소비하는 대신 한계효용이 높은 다른 재화를 소비하여 전체의 효용을 크게 할 것이다. 이때 각 재화의 1원어치의 한계효용이 모두 같아질 때 소비자가 느끼는 총효용은 극대화된다. 이처럼 모든 재화의 1원어치의 한계효용이 균등하게 되어 각 재화를 소비하는 양을 변화시킬 필요가 없는 경우를 ‘한계효용이 균등하다’라고 표현하고, 이를 ‘한계효용균등의 법칙’이라고 한다. 우측 그림은 효용 극대화가 충족된 상태이다.[9]
경제학 관점[편집]
오스트리아학파는 주류 경제학과 달리 심리학적 가정들을 이용하지 않고 순수 논리만으로 한계 효용 체감의 법칙을 논증한다. 예컨대 재화 5단위를 가지고 있는 한 사람을 예를들면, 이 사람은 이 재화 의 첫 번째 단위를 그 재화 가 봉사할 수 있는 목적 중에서 가장 시급하고 가장 높은 가치를 갖는 목적들에 먼저 사용할 것이다. 그렇게 된다면 당연히 재화 의 두 번째 단위는 그보다 덜 시급하고 덜 높은 가치를 갖는 목적들에 사용될 것이고, 세 번째, 네 번째, 다섯 번째 단위로 갈수록 점점 더 낮은 효용을 충족시키는 데 사용될 것이다. 그렇다면 마지막 단위가 가장 낮은 효용을 충족시키는 데 사용될 것이 명백한데, 이 단위를 바로 한계 단위(marginal unit)이라고 하고 이 한계 단위에 의해 제공되는 만족, 즉 이 한계 단위가 충족시키는 효용이 바로 한계 효용인 것이다. 그렇다면 이제 이 재화 가 더 많이 공급될수록, 즉 여섯 번째, 일곱 번째, 여덟 번째 단위가 추가될수록 한계 단위에 의해 제공되는 만족인 한계 효용은 당연히 논리적으로 하락할 수밖에 없다. 왜냐하면, 원래 다섯 번째 단위까지밖에 없었던 재화 가 세 단위 더 추가된다면, 이 경우에는 당연히 한계 단위인 여덟 번째 단위는 다섯번째 단위보다 덜 가치 있고 더 낮은 효용을 충족시키는 데 사용될 것이기 때문에이다.
한계 단위에 의해 제공되는 만족인 한계 효용은 하락하기 때문이다. 예를 들어 물 5병을 가지고 있는 사람이 있다면, 이 사람은 물 1병을 현재로서 가장 시급하고 가장 높은 가치를 가지는 목적을 충족시키는 데 먼저 사용할 것이다. 즉, 지금 몹시 목이 마르다면 먼저 물을 마시는데 사용할 것이다. 그렇다면 이제 그는 또 다른 물 1병을 그것보다 조금은 덜 시급하고 낮은 가치를 가지는 목적을 충족시키는데 사용할 것이다. 예를 들면, 세수 하거나 씻는 데 사용할 것이다. 마지막 단위인 물 1병은 그는 가장 낮은 효용을 충족시키는 데, 예를 들면 화초에 물을 주는 데 사용할 것이다. 이 경우, 한계 효용은 화초에 물을 줌으로써 얻는 효용이다. 만약 같은 조건에서 물 한 병을 가지고 있다면 이 경우 한계 효용은 물을 마심으로써 얻는 효용이다. 따라서 어떤 재화의 단위 공급이 증가할수록, 그 재화의 가장 마지막 단위로부터 얻어지는 효용인 한계 효용은 더 감소할 수밖에 없다. 행위자의 가치 척도에서 필연적으로 더 낮은 순위의 목적에 봉사하는 데 사용될 것이기 때문이다. 한계효용균등의 법칙은 다음과 같다.[10]
(m: 화폐 한 단위의 한계효용)
각주[편집]
- ↑ 기수적효용ㆍ서수적효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=13232&cid=43659&categoryId=43659
- ↑ 효용함수 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=779897&cid=42085&categoryId=42085
- ↑ 3.0 3.1 민윤지, 〈<제6강> 소비자이론(1) : 효용함수와 무차별곡선〉, 《동국대학교》, 2017-01-25
- ↑ 4.0 4.1 한계효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=388913&cid=41978&categoryId=41985
- ↑ 기대효용이론 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=1070786&cid=40942&categoryId=31819
- ↑ 스튜어드러셀, 피터노빅, 〈인공지능. 2: 현대적 접근방식 제3판〉, 《제이펍》, 2016-01-29
- ↑ 7.0 7.1 〈Ⅱ. 불확실성하에서의 선택이론과 유보가격 측정 모형〉, 《키리보험연구원》
- ↑ 8.0 8.1 젊은미소, 〈제 11 장. 한계효용이론〉, 《다음 블로그》, 2013-09-27
- ↑ 〈한계효용 균등의 법칙〉, 《시사경제신문》, 2015-03-05
- ↑ 한계효용체감의 법칙 나무위키 - https://namu.wiki/w/%ED%95%9C%EA%B3%84%20%ED%9A%A8%EC%9A%A9%20%EC%B2%B4%EA%B0%90%EC%9D%98%20%EB%B2%95%EC%B9%99?from=%ED%95%9C%EA%B3%84%ED%9A%A8%EC%9A%A9%EC%B2%B4%EA%B0%90%EC%9D%98%20%EB%B2%95%EC%B9%99
참고자료[편집]
- DeepBlue, 〈효용기반 의사결정 (Utility based Decision Making〉, 《네이버 블로그》, 2015-03-04
- 젊은미소, 〈제 11 장. 한계효용이론〉, 《다음 블로그》, 2013-09-27
- 한계효용 위키백과 - https://ko.wikipedia.org/wiki/%ED%95%9C%EA%B3%84%ED%9A%A8%EC%9A%A9
- 한계효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=388913&cid=41978&categoryId=41985
- 기대효용이론 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=1070786&cid=40942&categoryId=31819
- 다요소 효용 이론 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=271763&cid=41990&categoryId=41990
- 효용함수 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=779897&cid=42085&categoryId=42085
- 기수적효용ㆍ서수적효용 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=13232&cid=43659&categoryId=43659
- 크네이트, 〈기대효용 이론(expected utility theory)〉, 《네이버 블로그》, 2016-10-17
- 스튜어드러셀, 피터노빅, 〈인공지능. 2: 현대적 접근방식 제3판〉, 《제이펍》, 2016-01-29
같이 보기[편집]

 위키원
위키원









































![{\displaystyle E[U(x)]=\sum _{i=1}^{n}p_{i}U(x_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46451d2722df965d4fb902980cdeb83d8bfff8e3)




![{\displaystyle E[U(y)]=\sum _{j=1}^{m}q_{j}U(y_{j})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47b4bae5613d043549bac81f8bf3cfc625318fe1)
![{\displaystyle E[U(x)]>E[U(y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c3d48be80967fd3fed6340d31d73fe56b52129c)