제한 볼츠만 머신

제한적 볼츠만 머신

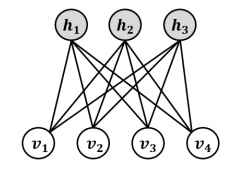
제한 볼츠만 머신(Restricted Boltzmann Machine, RBM)은 가시층 노드와 은닉층 간에 간선이 없는 볼츠만 머신이다. 심층신뢰신경망(DBN)을 구성하는 요소로 쓰인다. 첫번째 층은 우리가 볼 수 있는 층인 가시층(visible layer), 혹은 데이터가 입력되는 입력층이고 두번째 층은 특징값이 학습되는 은닉층이다.

개요

제한 볼츠만 머신은 1986년 폴 스몰렌스키(Paul Smolensky)에 의해 하모니움이라는 이름으로 처음 발명되었고, 2000년 중반 제프리 힌튼(Geoffrey Hinton)과 협력자들이 그들을 위한 빠른 학습 알고리즘을 발명하면서 유명해졌다. 제한 볼츠만 머신은 차원성 감소, 분류, 협업, 필터링, 기능 학습, 주제 모델링 및 많은 신체 양자역학에서 응용 프로그램을 발견했다. 제한 볼츠만 머신은 볼츠만 머신에서 층간 연결을 없앤 형태의 모델이다. 층간 연결을 없애면, 머신은 가시 유닛(Visible Unit)과 은닉 유닛(Hidden Unit)으로 이루어진 무방향 이분 그래프 형태의 모양이 된다. 결론적으로 모델의 층간 연결을 없앰으로써, 얻는 이점으로 뉴럴 네트워크는 깊어질 수 있었다. 가장 큰 이점은 가시 유닛이 관찰되고 고정(Clamped)되었을 때 은닉 유닛을 추론하는 마르코프 연쇄 몬테카를로 방법(MCMC; Markov chain Monte Carlo) 과정이 단 한 번에 끝난다는 것이다. 제한 볼츠만 머신은 확률모델의 계산이 불가능하기 때문에, 학습시 근사법인 마르코프 연쇄 몬테카를로 방법 또는 제프리 힌튼 교수가 발견한 CD를 사용하는데, 제한 볼츠만 머신의 모델의 간단함에서 오는 추론에 대한 이점은 샘플링 근간의 학습법이 실용적인 문제에 적용되는데 기여했다.

제한 볼츠만 머신은 심층신뢰신경망의 기본 뼈대가 된다. 제한 볼츠만 머신을 쌓아올리면서(Stacking), 그리디하게 학습함으로써 심층신뢰신경망을 완성한다. 심층신뢰신경망을 아는 사람은 기본적으로 제한 볼츠만 머신은 무방향이기에, 제한 볼츠만 머신이 방향성 있는 모델인 심층신뢰신경망이 되는지 의아할 것이다. 이는 제프리 힌튼(Jeffrey Hinton)의 제자의 우연 발견적인 연구 성과인데, 원래 힌튼 교수는 그래픽 모델이 방향성을 가질 때 생기는 익스플레이닝 어웨이(Explaining Away) 효과 때문에 학습이 매우 어려워 연구를 무방향성 모델로 선회했다가, 제한 볼츠만 머신을 쌓으면, 다층 제한 볼츠만 머신이 되는 것이 아니라, 심층신뢰신경망과 비슷해진다는 사실을 발견하게 된다. 이 발견은 심층신뢰신경망 학습을 단순히 여러 개의 제한 볼츠만 머신 학습으로 환원시킴으로써 어려운 심층신뢰신경망 학습의 복잡도를 층의 갯수에 비례하는 복잡도로 낮추었다. 이는 선행학습(Pre-training) 과 미세조정(fine-tuning) 의 새로운 학습 패러다임으로 발전하게 된다.

심층신뢰신경망은 비지도 방식으로 계층마다 학습을 진행하는데, 이때 각각의 계층은 보통 제한 볼츠만 머신의 형태를 띄고 있다. 제한 볼츠만 머신은 에너지 기반의 생성 모형으로 가시 유닛과 은닉 유닛으로 이루어진 무방향 이분 그래프 형태이다. 가시 유닛들과 은닉 유닛들 사이에만 연결이 존재한다. 제한 볼츠만 머신이 훈련되고 나면 다른 제한 볼츠만 머신이 그 위에 쌓아 올려짐으로써 다중 계층 모형을 형성한다. 제한 볼츠만 머신이 쌓아 올려질 때마다, 이미 훈련된 제한 볼츠만 머신의 최상위 계층이 새로 쌓이는 제한 볼츠만 머신의 입력으로 쓰인다. 이 입력을 이용하여 새 제한 볼츠만 머신이 훈련되고, 원하는 만큼의 계층이 쌓일 때까지 해당 과정이 반복된다.

구조

제한 볼츠만 머신은 같은 층 내부의 연결이 전혀 없으며, 이 구조 때문에 ‘제한된’ 볼츠만 머신이라는 이름이 붙여졌다. 입력층의 노드는 데이터를 입력받으면 입력받은 데이터를 은닉층에 얼마나 전달할 것인지를 확률에 따라 결정(stochastic decision)한다. 즉 확률에 따라 입력을 전달할지 혹은 전달하지 않을지를 결정한다.

각 입력 노드는 데이터의 저수준 특징값 혹은 속성을 받아온다. 예를 들어 흑백 이미지가 입력 데이터라면 각 입력 노드는 이미지의 픽셀 값에 해당한다. 만일 MNIST 데이터베이스를 사용한다면 입력 노드의 개수는 데이터베이스의 이미지의 픽셀 수(784)와 같게 설정된다.

입력으로 $x$를 넣으면 그 은닉층의 노드에 있는 가중치 $w$와 곱해진다. 그리고 $bias(b)$를 더한 값$(w*x+b)$을 활성함수 $f()$에 넣은 것이 노드의 출력이 된다.

 $activationf((weightw*inputx)+biasb)=outputa$

위의 식은 은닉 노드 하나에 들어오는 여러 개의 입력 중 하나만 고려한 식이다. 실제로는 여러 입력 노드의 값을 받아서 각자 다른 가중치 $w$와 곱해진다. 그리고 그 총합에 바이어스를 더한 뒤 활성함수에 들어간다. 즉 $f(x_{1}*w_{1}+x_{2}*w_{2}+x_{3}*w_{3}+x_{4}*w_{4}+b)$가 은닉 노드의 출력이다. 이렇게 모든 가시층의 노드가 모든 은닉 노드로 전달되는 것 특징 때문에 제한 볼츠만 머신은 대칭 이분 그래프(symmetrical bipartite graph)라고 부른다. 즉, 두 층이 대칭적으로 모두 연결되어 있어 있는 그래프인 것이다. 4개의 입력 노드는 3개의 은닉 노드에 모두 연결되어 있다. 그리고 각 연결마다 각자 다른 가중치 값이 있다. 따라서 총 12개(4*3)의 가중치가 있다. 이런 경우에 일반적으로 이 가중치를 4x3 행렬로 나타낸다. 위에서 설명한 계산은 모든 은닉 노드에서 일어난다. 즉 각 은닉 노드마다 4개의 입력 값에 적당한 가중치를 곱해 그 값을 더한다. 그리고 거기에 바이어스를 더한 뒤 이를 활성 함수에 통과시킨다. 심층신경망이라면 계속 층을 쌓아서 전체 신경망 구조를 만든다. 그리고 최종적으로 출력층에서 데이터를 분류하는 등의 작업을 수행한다.

가중치 갱신

제한 볼츠만 머신 훈련 과정에서의 가중치 갱신은, 다음의 식을 기반으로 경사 하강법을 통해 이루어진다.

 $\Delta w_{i,j}(t+1)=w_{i,j}(t)+n{\frac {(\alpha log(p(v)))}{\alpha w_{i,j}}}$

여기서 $p(v)$ 는 다음의 식으로 주어지는 가시 벡터의 확률을 나타낸다.

 $p(v)={\frac {1}{Z}}\sum _{h}e-E(v,h)Z$

위 식은 정규화를 위해 사용되는 분배함수(partition function)이며, E(v, h) 는 신경망의 상태(state)에 부여되는 에너지 함수이다. 에너지가 낮을수록 해당 신경망이 더 적합한 상태임을 의미한다.

 ${\frac {\alpha log(p(v))}{\alpha w_{i,j}}}$

기울기는 좀 더 간단하게 표현된다.

 $<u_{i}h_{j}>data-<u_{i}h_{j}>model$

이 때 $<\cdots >p$는 분포 $p$에 관한 평균을 의미한다. $<u_{i}h_{j}>model$을 샘플링 하려면 올터네이팅 깁스 샘플링(alternating Gibbs sampling)을 매우 많이 반복해야 하기 때문에 CD에서는 올터네이팅 깁스 샘플링을 n회만 반복한다. 실험을 통해 n = 1 일 경우에도 충분한 성능이 나온다고 알려져 있다. n회 반복 후 샘플링 된 데이터가 $<u_{i}h_{j}>model$를 대신한다.

CD 수행 과정

CD 수행 과정은 다음과 같다.

1. 가시 유닛들을 훈련 벡터로 초기화 한다.

2. 다음의 가시 유닛들이 주어지면 은닉 유닛들을 모두 동시에 갱신한다.

 $p(h_{j}=1|V)=$σ$(b_{j}+\sum _{i}u_{i}w_{i,j})\cdot$ σ

3. 다음의 은닉 유닛들이 주어지면 가시 유닛들을 모두 동시에 갱신한다.

 $p(u_{i}=1|H)=$σ$(a_{j}+\sum _{j}h_{j}w_{i,j})\cdot a_{i}$

위 식은 $u_{i}$의 편향이다. 이 부분을 복원(reconstruction)이라고 부른다.

4. 복원된 가시 유닛들이 주어지면 (2)에서 쓰인 식을 이용하여 은닉 유닛들을 모두 동시에 다시 갱신한다.

5. 다음과 같이 가중치를 갱신한다.

 $\Delta w_{i,j}$∝ $<u_{i}h_{j}>data-<u_{i}h_{j}>reconstruction$

특징

재구성

제한 볼츠만 머신을 이용한 비지도학습(unsupervised learning)이 있다. 비지도학습은 데이터의 라벨을 학습하는 것이 아니라 입력 데이터만을 가지고 수행하는 작업을 의미한다. 여기서 수행할 작업은 재구성(reconstruction)이다. 데이터를 제한 볼츠만 머신에 입력하고 학습시키면 제한 볼츠만 머신이 데이터를 스스로 재구성할 수 있게 된다. 재구성 과정은 위에서 설명한 과정의 반대 방향으로 진행된다. 은닉층의 값을, 위와 같은 12개의 가중치를 이용해 입력 노드로 전달하고 입력 노드에서는 그 값을 다 더한다. 그리고 거기에 바이어스를 더한 값이 은닉층을 이용해 재구성한 입력이 된다. 이 값은 입력값의 근사치이다. 학습이 일어나기 전에는 가중치를 임의의 값으로 초기화한다. 따라서 이렇게 재구성한 값은 실제 입력값과 많이 다를 수 있다. 재구성한 값과 입력값의 차이는 오차가 된다. 이 오차는 다른 인공 신경망 학습과정과 마찬가지로 백프롭(backprop)된다. 그리고 제한 볼츠만 머신의 학습은 위의 두 과정을 반복하면서 점점 오차를 줄여나간다. 입력 데이터로 은닉층의 값을 추정하는 과정은 $w$가 주어졌을 때 입력 $x$에 대한 은닉층 $a$의 조건부 확률 $p(a|x;w)$이 된다. 반대로 재구성 단계는 $w$가 주어졌을 때 은닉층 $a$에 대한 입력 $x$의 조건부 확률, 즉 $p(a|x;w)$를 추정하는 과정이다. 결과적으로 두 추정치는 입력과 은닉층의 결합확률분포 $p(x,a)$의 추정이다.

재구성은 회귀나 분류와는 다르다. 재구성은 입력 데이터의 확률 분포를 추정하는 과정, 즉 생성 모델을 학습(generative learning)하는 과정으로, 입력-출력의 관계를 찾는 분류 모델(discriminative learning)과 다르다. 입력 데이터와 재구성한 추정치의 분포가 아래 그림의 $p(x)$와 $q(x)$처럼 겹치는 구간이 있지만 완벽하게 일치하지는 않는 경우라고 가정해 보겠다. 제한 볼츠만 머신에서는 두 분포가 얼마나 유사한지 측정하는 방법으로 쿨백-라이블러 발산(Kullback Leibler Divergence)을 사용한다. 두 확률 분포가 겹치지 않는 부분이 있는데, 이를 발산(divergence)이라고 한다. 제한 볼츠만 머신의 최적화는 이 발산이 최소화되도록 하는 알고리즘이. 따라서 최적화는 두 분포를 유사하게 만들어주는 과정이다. 또한 이 최적화 과정은 가중치 $w$를 맞춰주는 과정이다. 이렇게 가중치가 조절되면 가중치와 입력을 곱한 값인 은닉층의 값도 서서히 변해간다. 결과적으로 은닉층은 입력층을 나타내는 특징값(feature)이 되고, 학습이 잘 된 특징값과 가중치를 이용해 입력층을 근사하면 실제 입력과 유사한 확률 분포가 된다.

확률 분포

확률 분포

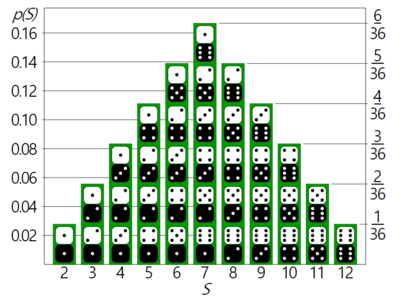
그림을 보면 두 수의 합이 7이 될 확률이 가장 높다. 그리고 이 값을 추정하려면 7이 될 확률이 가장 높다는 사실을 참고해야 할 것이다. 언어를 구성하는 글자는 각자 다른 확률 분포를 갖는다. 예를 들어 영어에서는 e, t, a가 많이 나온다. 한편 아이슬란드어에서는 a, r, n이 가장 자주 나온다. 따라서 다른 언어를 모델링하려면 이런 분포를 고려해야 한다. 마찬가지로 이미지 데이터를 모델링하려면 각 픽셀의 값이 어떤 분포를 가지는지 알아야 한다. 제한 볼츠만 머신에 코끼리 사진과 개 사진을 입력했다고 가정해 보겠다. 입력 값을 토대로 은닉층을 구하는 과정에서 제한 볼츠만 머신은 이 입력 데이터를 보고, 코끼리를 나타내는 은닉 노드와 개를 나타내는 은닉 노드중에 어디에 더 강한 신호를 보내야 하는지, 즉 가중치를 결정한다. 그리고 재구성 단계에서는 코끼리 은닉 노드의 값이 큰데, 이런 경우엔 픽셀의 분포가 어떤식인지를 결정한다. 이를 x가 주어졌을 때 a의 분포인 조건부 확률과, 반대로 a가 주어졌을 때 a의 분포인 조건부 확률을 합친 결합 확률 분포(joint probability distribution)가 된다.

재구성을 학습하는 과정은 어떤 픽셀들이 동시에 큰 값을 지니는지 그 경향을 학습하는 과정이다. 예를 들어 코끼리 사진이라면 코끼리의 모습 - 길고 구부러진 코, 큰 귀, 다리 - 등의 중요한 특징을 학습한다. 제프리 힌튼은 이것을 기계가 꿈을 꾸는 것이라고 표현했다. 이런 시각화로 우리는 제한 볼츠만 머신의 학습이 잘 이루어지는지 확인할 수 있다.

심층 구조

제한 볼츠만 머신의 은닉층의 학습이 끝나고 나면 이 데이터는 다시 다음 층으로 연결된다. 두 번째 연결에서는 은닉층이 가시층의 역할을 하고, 새로운 추가한 층이 은닉층이 된다. 즉, 첫 번째 연결에서 은닉층이 학습한 내용을 가지고 다시 새로운 제한 볼츠만 머신을 학습하는 것이다. 이렇게 연달아 은닉층을 잇고 학습하는 것이 각자 다른 층위의 특징값(feature hierarchy)을 학습하는 과정이다. 심층신경망은 이런 구조로 더 추상적이고 복잡한 데이터를 이해한다. 은닉층을 새로 추가할 때마다 기존 층의 데이터를 근사할 수 있도록 가중치의 학습이 이루어진다. 이런 과정을 층별 탐욕 비지도 선행학습(layerwise, greedy unsupervised pre-training)이라고 한다. 각 층마다 최대한 오차를 줄이는 방향으로 학습이 이루어지기 때문에 층별 탐욕 학습이고, 이 모든 과정이 라벨의 정보가 없이 입력 데이터만을 가지고 이루어지기 때문에 비지도 학습이라고 한다. 그리고 이 학습한 결과를 다시 다른 학습에 쓸 수 있기 때문에 선행학습이라고 부른다. 이렇게 선행학습이 된 가중치는 데이터의 분포를 이미 알고있기 때문에 이 값으로 초기화한 심층 신뢰 신경망은 더 좋은 성능을 보여 준다. 제한 볼츠만 머신의 광범위한 활용 사례 중에서도 특히 선행학습이 아주 유용하다. 선행학습은 가중치를 학습시킨다는 의미에서 역방향전파(backpropagation)와 유사한 역할을 한다.

연속 제한 볼츠만 머신

연속 제한 볼츠만 머신(CRBM, continuous RBM)은 입력 값으로 연속적인 값을 사용할 수 있는 제한 볼츠만 머신이다. 연속 제한 볼츠만 머신도 일반적인 제한 볼츠만 머신처럼 컨스트래스티브 다이버전스(constrastive divergence)를 사용하지만 그 형식이 조금 다르다. 연속 제한 볼츠만 머신을 쓰면 이미지 픽셀을 0에서 1 사이의 값으로 바꿔서 처리할 수 있다. 잠시 심층 신경망의 구성 요소를 다시 짚고 넘어가면, 심층신경망은 입력, 계수, 바이어스, 활성함수로 구성되어 있다. 입력은 한 단계 앞에 있던 층에서 (혹은 입력 데이터에서) 받아오는 값이다. 계수(coefficient)는 가중치(weights)라고도 하는데, 말 그대로 입력에 적용되는 가중치이다. 바이어스는 입력의 가중치합에 더해지는 값으로 ‘y 절편’과 비슷하며 노드의 값에 오프셋을 주어서 노드가 활성화되도록 돕는다. 활성함수는 최종적으로 출력에 적용되는 값으로 연산에 비선형성(nonlinearity)을 더한다. 이 네 가지 구성 요소는 층마다 다르게 설정되기도 한다. 연속값을 취하는 제한 볼츠만 머신은 가시층엔 가우시안 함수(Gaussian transformations)를, 은닉층엔 ReLU(rectified linear unit)를 활성함수로 쓴다. 특히 이 설정은 얼굴 이미지 재구성에서 좋은 결과를 보여주었다. 이진값(binary data)를 다루는 경우라면 두 층의 활성 함수도 두 종류의 값만 출력하게 된다. 은닉층에서는 가우시안 활성함수를 잘 쓰지 않는다. 이진값을 가우시안 함수에 넣는 것보다 ReLU 함수를 쓰는 경우가 더 좋은 결과를 보여주기 때문이다.

참고자료

• Restricted Boltzmann machine Wikipedia - https://en.wikipedia.org/wiki/Restricted_Boltzmann_machine
• 딥러닝 위키백과 - https://ko.wikipedia.org/wiki/%EB%94%A5_%EB%9F%AC%EB%8B%9D
• 딥러닝에서 사용되는 알고리즘 TCP스쿨 - http://tcpschool.com/deeplearning/deep_algorithm3
• Chris Nicholson, 〈초보자용 RBM(Restricted Boltzmann Machines) 튜토리알〉, 《pathmind》

같이 보기

• 딥러닝
• 심층신뢰신경망

이 제한 볼츠만 머신 문서는 인공지능 기술에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

인공지능 : 인공지능 서비스, 인공지능 로봇, 인공지능 기술 □■⊕, 인공지능 기업, 인공지능 인물 인공지능 기술 AI 워싱 • 랭체인 • 로봇공학 • 로봇기술 • 인지과학 • 자동추론 • 자연어 처리 • 지능 • 지식표현 • 컴퓨터 비전 • 튜링 테스트 • 프롬프트 • 프롬프트 엔지니어링 문자인식과 음성인식 ICR • OCR • OMR • TTS • URL • 글자 • 답변 • 대화 • 동영상 • 디자인 • 맥락 • 문서 • 문자 • 문자인식 • 문자채팅 • 발음 • 번역 • 분류 • 상담 • 소스코드 • 스토리 • 얼굴 • 얼굴인식 • 음성 • 음성채팅 • 음성인식(STT) • 이미지 • 인공어 • 자막 • 자연어 • 질문 • 채팅 • 코드 • 코딩 • 텍스트 • 통번역 • 통역 • 파일 • 폴더 • 화상채팅 • 화자인식 인공지능 데이터 데이터라벨러 • 데이터라벨링 • 데이터셋 • 벡터 • 벡터DB • 벡터공간 • 스칼라 • 임베딩 • 크라우드워커 • 토큰 • 토큰화 인공지능 학습 ADP • CoLLM • DALL-E • DDPG • DQN • LAM • LMM • SARSA • sLLM • SLM • 강화학습 • 거대언어모델(LLM) • 결정이론적 메타추론 • 계통적 강화학습 • 과적합 • 동적 계획법 • 딥러닝 • 딥큐러닝 • 머신러닝(기계학습) • 메타추론 • 모델 기반 강화학습 • 모델 프리 강화학습 • 미세조정(파인튜닝) • 반영식 아키텍처 • 비지도학습 • 사전학습 • 수시 알고리즘 • 어니 • 에이전트 • 인공지능 학습 • 전이학습 • 준지도학습 • 지도학습 • 추론 • 학습 • 확률적 경사하강법 인공지능 알고리즘 AGI • ANI • ASI • RAG • XAI • 가중치 • 관계형 네트워크(RN) • 뉴런 • 다층퍼셉트론 • 단층퍼셉트론 • 데이터마이닝 • 방사신경망 • 볼츠만 머신 • 분산 샌드박스 • 생성대립신경망(GAN) • 생성형 AI • 수퍼얼라인먼트 • 순전파 • 순환신경망(RNN) • 시그모이드 함수 • 신경망 • 신경망 구조 • 심층신경망(DNN) • 심층신뢰신경망(DBN) • 양방향 비고정값 암호 체계(TSID) • 역전파 • 은닉층 • 인공신경망(ANN) • 인공지능(AI) • 제한 볼츠만 머신(RBM) • 전방전달신경망 • 주의 메커니즘 • 코헨 자기조직 신경망 • 텍스트마이닝 • 트랜스포머 • 파이 • 퍼셉트론 • 합성곱 신경망(CNN) 계산복잡도 NP • NP-완전 • 계산복잡도 • 공간복잡도 • 시간복잡도 • 여 NP • 여 NP-완전 인공지능 프로그램 BCI • GPT • 딥블루 • 딥페이크 • 멀티모달 AI • 모달 • 모달리티 • 모달창 • 알렉스넷 • 어니 • 알파고 • 알파고제로 • 알파폴드 • 왓슨 • 카페 • 컨트롤넷 • 텐서플로 • 텔레파시 • 토치 • 파이토치 • 한돌 인공지능 특징 결정이론 • 계산상의 합리성 • 논리학 • 논리주의자 • 분산성 • 불확실성 • 삼단논법 • 선호도 • 예측곤란성 • 완벽한 합리성 • 유계 합리성 • 이유 불충분의 원리 • 자율성 • 최대기대효용 • 할루시네이션 • 효용이론 인공지능 법적 지위 권리주체성 • 소버린 AI • 전자대리인 • 전자적 인간 • 책임법 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반