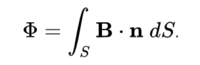자속
자속(magnetic flux, 磁束)은 어떤 가상의 곡면에 작용하는 총 자기력을 나타내는 물리량으로서, 곡면의 넓이와 곡면에 대하여 수직인 자기장 성분의 곱이다. 그 국제 단위는 웨버(Wb)이고, 통상적인 기호는 그리스 대문자 Φ 또는 ΦB이다. 자기 다발 또는 자기력선속(磁氣力線束)이라고도 한다.
개요[편집]
자속은 어떤 표면을 수직으로 통과하는 자기력선의 수이다.
크기와 방향이 균일한 자기장 B가 있다. 자기력선이 자기장과 수직이고 면적이 A인 평면을 통과할 때 단위면적을 지나는 자기력선의 수는 자기장의 크기 B에 비례한다. 따라서 면적 A인 표면을 통과하는 선의 수는 B*A에 비례한다. 이때 자기장의 세기 B와 자기장에 수직인 면적 A의 곱 B*A를 이 표면적을 지나는 자속이라고 한다.
만약 평면이 자기장에 수직이 아니라면 자기력선의 수는 B*A보다 작다. 평면의 법선과 자기장이 이루는 각이 θ일 때, 자속은 B*A*cosθ이다. 따라서 자기장과 면이 서로 수직일 때 자속은 B*A로 가장 큰 값을 가지며, 자기장과 표면적이 서로 평행일 때 0으로 가장 작은 값을 가진다.
일반적인 모양의 구부러진 표면을 지나는 자속을 구하려면 그 면을 잘게 나누어서 각각의 조그만 면이 평면에 가까워지도록 만든 다음, 조그만 면을 지나는 자속을 전부 더하여 전체 자속을 구한다.
자속의 단위는 웨버(Wb) = 1T·㎡이며, 이때 T(테슬라)는 자기장의 단위이다.
정의[편집]
자기장 B가 있는 공간 상의 곡면 S와 그 둘레를 이루는 폐곡선 C를 생각하자. S의 무한소 면적 요소 dS에 대하여 수직인 단위 벡터를 n이라고 하자. 그렇다면 곡면 S를 지나는 자기 선속 Φ는 다음과 같은 적분의 값이다.
가우스의 자기 법칙에 따라, 자기력선은 중간에 끊어지거나 없어지지 않는다. 즉,
∇ ∙ B = 0
여기서 ∇∙은 벡터장의 발산을 나타낸다. 이에 따라, 서로 다르지만 그 둘레가 같은 곡면의 자기 선속은 같으며, 곡면의 자기 선속은 그 둘레를 통과하는 자기력선의 수로 생각할 수 있다. 곡면을 약간 바꾸어도 그 둘레가 바뀌지 않으면 곡면을 통과하는 자기력선의 수는 바뀌지 않는다.
자기 선속은 넓이와 자기장의 곱이므로, 그 단위는 넓이의 단위와 자기장의 단위의 곱이다. 국제단위계에서는 자기장의 단위가 테슬라이므로, 자기 선속의 국제 단위인 웨버는 다음과 같다.
CGS 단위계에서 자기 선속의 단위는 맥스웰(Mx)이다.
자기 선속의 크기가 변화하면 그 변화 속도에 비례하는 크기의 전기장이 발생한다. 자기장은 전기장의 시간적 변화에 따라 유도되므로, 이러한 전기장과 자기장(또는 전기력선과 자기력선)의 상호 유도가 일어나게 된다. 이렇게 하여 일종의 파동이 발생하게 되는데, 이를 전자기파라 한다.
자기 선속의 양자화[편집]
원환 꼴의 초전도체가 있다고 하자. 초전도체의 내부에는 마이스너 효과에 의해 내부에 자기 선속이 통과할 수 없지만, 원환의 구멍에 해당하는 부분에는 자기 선속이 통과할 수 있다. 이 구멍을 지날 수 있는 자기 선속은 아로노프-봄 효과와 패러데이 법칙에 의해
Φ₀ = h/2e = 2.067833758(46) × 10⁻¹⁵Wb
의 정수배로 양자화된다. (여기서 h는 플랑크 상수, e는 기본 전하량이다.)
참고자료[편집]
같이 보기[편집]

 위키원
위키원