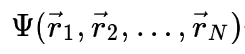양자화학
양자화학(量子化學, Quantum chemistry)이란 화학의 분야 중 하나로, 양자역학의 여러 원리를 화학의 여러 문제에 적용하여 원자와 전자의 움직임부터 분자구조와 물성 또는 화학 반응을 이론적으로 설명하는 학문 분야이다.
개요[편집]
양자화학은 양자역학 이론을 이용해서 원자와 분자의 여러 가지 물리적, 화학적 성질, 화학적 현상, 그리고 화학 반응을 이론적으로 설명하는 화학의 한 분야이다. 양자화학의 주요 관심은 원자와 분자의 전자 구조, 화학 결합, 분자 사이 상호 작용, 반응 경로, 동역학 등에 대한 이론과 계산 방법론을 발전하는 것이다.
양자화학은 분광학이나 열역학 데이터, 화합물의 반응성이나 반응 속도 등과 같이 실험 측정 결과를 해석하고 이해하는 강력한 도구이다. 또한, 양자화학은 관찰이나 측정이 어려운 반응의 전이 상태나 중간체에 대한 정보를 얻는 목적에도 많이 이용되며, 아직 관찰되지 않은 성질이나 거동을 예측하거나 탐색하는 목적에도 이용된다.
양자화학은 기본적으로 슈뢰딩거 방정식(Schrödinger equation)의 해를 구하는 것을 목표로 한다. 그러나 소수의 간단한 원자로 이루어진 계를 제외하고는 그 방정식의 정확한 해를 구하는 것은 매우 어렵다. 대부분은 여러 가지 가정, 근사, 그리고 방대한 계산이 필요하다. 양자 화학 발전의 초기 분자에 대한 양자 화학적 계산에 한계가 있었으나, 1950년대에 전자 컴퓨터가 활용되기 시작하면서 본격적으로 양자 화학 계산의 진전이 이루어졌다. 그러나 양자 화학에서 다루는 계가 커짐에 따라 양자 화학 계산에서의 계산량은 계속 증가하여 양자 화학 계산의 정확도와 계산 비용 사이에 적절한 균형을 잡는 것은 여전히 중요하다.
지난 수십 년에 걸쳐 이루어진 급격한 컴퓨터의 연산 능력의 향상, 컴퓨팅 자원의 증가, 그리고 계산 방법론의 발전에 힘입어 과거에는 양자 역학적 접근이 어려웠던 거대한 분자나 많은 분자로 이루어진 복잡한 화학계에 대한 양자 화학적 계산이 가능해졌다. 근래에 컴퓨터의 발전과 함께 계산 화학(computational chemistry) 분야가 빠르게 정립되고 있다. 양자 화학은 계산화학 분야의 중요한 부분이다.
역사[편집]
양자 역학 이론을 최초로 화학적 문제에 응용은 1927년 독일의 물리학자 하이틀러(Walter Heitler)와 런던(Fritz London)이 원자가 결합(valence bond) 개념을 이용하여 수소 분자에 대해 계산하여 공유 결합의 근원을 설명한 것으로 알려져 있다.
1930년대 초에 미국의 물리학자 슬레이터(John C. Slater)와 화학자 폴링(Linux L. Pauling)은 하이틀러와 런던의 이론을 원자가 결합 이론(valence bond theory)으로 발전시켰다. 특히 폴링은 1931~1933년에 발표한 유명한 논문 'The Nature of the Chemical Bond'에서 혼성화(hybridization)와 공명(resonance) 개념을 도입하여 원자가 결합 이론을 확장하는 데 기여하였다.
원자가 결합 이론이 한창 개발되고 있던 1928년, 독일의 물리학자 훈트(Friedrich Hund)와 미국의 물리학자이자 화학자 멀리켄(Robert S. Mulliken)은 분자의 전자 구조를 다루기 위한 또 다른 방법으로 분자 오비탈 이론(molecular orbital theory)을 제안하였다. 1929년 영국의 수학자이자 물리학자 레너드-존스(Sir John Lennard-Jones)는 최초로 이원자 분자에 대한 오비탈을 계산하여 산소 분자의 상자기성(paramagnetism)을 설명하였다.
1927년 영국의 물리학자 하트리(Douglas R. Hartree)는 다전자 원자나 이온에 대한 근사적 파동 함수와 에너지를 얻는 하트리 방법(Hartree method)을 고안하였다. 하트리는 실험적 파라미터 없이 슈뢰딩거 방정식의 해를 구하는 순이론적(ab initio) 방법을 개발하였다. 하트리 방법은 1930년 슬레이터와 러시아의 물리학자 폭(Vladimir A. Fock)이 지적한 파동 함수의 반대칭 조건을 만족하도록 하트리-폭 방법(Hartree-Fock method)으로 다시 정리되었다.
1951년 네덜란드의 물리학자이자 화학자 로탄(Clemens C. J. Roothaan)은 분자 오비탈 계산을 위한 하트리-폭 방정식(Hartree-Fock equation)을 바탕 함수 집합(basis set)을 이용하는 행렬 형태로 유도하여 컴퓨터를 이용한 계산에 적합하게 만들었다.
가우시안 70(Gaussian 70)은 영국의 이론 화학자 포플(Sir John A. Pople)과 그의 연구원이 하트리-폭 계산을 빠르게 실행할 수 있는 새로운 알고리즘을 개발하여 1970년에 배포한 양자 화학 계산 프로그램이다. 가우시안 70은 속도와 편의성으로 이론 화학을 전공하지 않는 화학자도 사용했던 최초의 순이론적 계산 프로그램이었으며 현재까지도 계속 업데이트되어 가장 널리 사용되고 있다.
양자 화학 계산의 반실험적 방법(semi-empirical method)의 시초는 1930년 독일의 물리학자 휘켈(Erich Hückel)이 콘쥬게이션 분자에서 π-전자의 분자 오비탈과 에너지를 얻기 위하여 제안한 휘켈 방법(Hückel method)이다.
1950년대에 미국의 화학자 파(Robert G. Parr), 파리저(Rudolph Pariser), 그리고 독립적으로 영국의 포플은 π-전자계의 전자 스펙트럼과 전자 구조를 예측하기 위한 반실험적 방법인 파리저-파-포플 방법(Pariser-Parr-Pople method)을 개발하였다.
1965~1967년에 포플은 반실험적 분자 오비탈 계산 방법인 CNDO와 INDO 방법을 개발하였다. 미국의 화학자 듀어(Michael J. S. Dewar)는 1970대와 1980대에 걸쳐 MINDO, MNDO, AM1, PM3 등과 같은 여러 가지 반실험적 방법을 개발하였으며, 1970년대에는 수십 개의 원자로 이루어진 분자의 구조와 반응 메커니즘에 대한 정량적인 계산이 가능하게 되었다.
모팩(MOPAC)은 1981년 듀어 그룹에서 배포한 여러 가지 반실험적 방법을 이용한 양자 화학 계산 프로그램이다. 모팩은 충분히 큰 분자에 대한 순이론적 계산이 가능해지기 전까지는 실질적인 크기의 유기 분자의 구조와 반응을 다룰 수 있는 프로그램으로 인기가 있었다.
전자 구조 계산[편집]
양자 화학적 문제를 다루는 첫 단계는 보통 본-오펜하이머 근사(Born-Oppenheimer approximation)에서 분자의 전자에 대한 시간-독립 슈뢰딩거 방정식(time-independent Schrödinger equation)을 풀어서 분자 오비탈과 에너지, 분자의 총 에너지와 전자 밀도 등을 구하는 것인데, 이로부터 분자의 전자 구조를 결정한다고 말한다.
그러나 두 개 이상의 전자를 포함하는 분자에 대한 슈뢰딩거 방정식의 정확한 해1)는 얻을 수 없고, 근사적인 방법을 사용해야 한다. 슈뢰딩거 방정식의 근사적 해를 구하는 것은 아주 방대한 계산량을 요구하므로 전자 구조 계산에는 전자 컴퓨터의 이용이 필수적이다. 실제로 전자 구조 계산은 과학의 전 분야 중에서 가장 많은 컴퓨팅 자원을 요구하는 분야의 하나이다.
분자의 전자 구조를 다루기 위한 이론은 크게 세 부류, 즉 원자가 결합 이론, 분자 오비탈 이론, 밀도 범함수 이론으로 구분할 수 있다.
원자가 결합 이론[편집]
원자가 결합 이론의 뿌리는 전자쌍 결합(electron-pair bonding)을 기반으로 하는 루이스 이론(Lewis theory)에서 찾을 수 있다. 원자가 결합 이론에서 결합은 한 원자의 원자 오비탈과 또 다른 원자의 원자 오비탈 사이의 겹침에 의해 형성되며, 결합 전자쌍은 두 원자 사이에 '편재된(localized)' 것으로 간주한다. 원자가 결합 이론은 한 원자의 원자 오비탈들이 '혼합'되어 혼성 오비탈(hybrid orbital)을 형성하는 혼성화(hybridization) 개념과 전자의 비편재화를 설명하기 위한 공명(resonance) 개념을 통하여 더 복잡한 분자의 결합과 구조를 설명할 수 있도록 확장되었다.
현대의 원자가 결합 이론에서는 결합 전자쌍이 두 원자 사이에 편재되어 있다는 생각을 고수하지 않고 분자 전체로의 비편재화를 허용한다.
원자가 결합 이론은 분자 오비탈 이론보다 컴퓨터를 이용한 계산 알고리즘에는 불리하지만, 화학자의 결합에 대한 직관적인 생각에 더 가깝기 때문에 여전히 많이 사용되고 있다.
분자 오비탈 이론[편집]
분자 오비탈 이론(molecular orbital theory)에서는 분자의 전자를 개별적인 분자 오비탈로 나타낼 수 있다고 가정하고, 분자의 전자 파동함수를 이들 오비탈의 곱으로 나타낸다. 분자마다 고유한 분자 오비탈들의 집합이 있으며, 이는 하트리-폭 방법(Hartree-Fock method)으로 구할 수 있다.
분자 오비탈 이론은 원자가 결합 이론과는 달리 각 전자는 어느 특정한 결합에 편재되어 있지 않고 분자 전체에 퍼져 있으며, 즉 '비편재화되어(delocalized)' 있으며, 하나의 결합에 특정한 전자쌍이 아니라 분자의 모든 전자가 관여하는 것으로 간주한다.
분자 오비탈 이론은 원자가 결합 이론보다 더 다양하고 복잡한 분자들의 전자 구조와 특성을 설명할 수 있는데, 특히 분자의 들뜬 전자 상태, 전자 스펙트럼, 이온화 에너지와 광전자 스펙트럼 등의 계산에 유리하다. 또한, 분자 오비탈 이론은 수학적으로 컴퓨터를 이용한 계산 알고리즘에 좀 더 적합하므로 순이론적 계산이나 대규모의 분자 계산에 널리 응용되고 있다.
분자 오비탈을 계산하는 하트리-폭 방법에서는 전자 상관(electron correlation)이 무시되었기 때문에 더 정확한 전자 구조를 계산하기 위해서는 이것이 포함된 하트리-폭 이후 방법(post Hartree-Fock methods)이 필요하다. 몇 가지 대표적인 하트리-폭 이후 방법에는 배치 사이 상호작용(configuration interaction), 묄러-플레셋 섭동론(Mфller-Plesset perturbation theory), 결합 클러스터 이론(coupled-cluster theory), 다배치 자체 일관성 장 방법(multi-configurational self-consistent field method) 등이 있다.
밀도 범함수 이론[편집]
다전자 계에 대한 슈뢰딩거 방정식의 해를 구하기 위한 하트리-폭 방법과 하트리-폭 이후 방법은 모두 파동 함수에 기반을 두고 있고, 계의 성질은 전자 파동 함수에 의한 기대값으로부터 결정할 수 있다.
밀도 범함수 이론(density functional theory, DFT)은 다전자 계의 성질은 전자 밀도(electron density)에 의하여 유일하게 결정된다는 호헨베르크-콘 정리(Hohenberg-Kohn theorem)에 기반을 두고 있다. 예를 들어, 계의 바닥 상태 에너지 E₀는 바닥 상태 전자 밀도 ⍴₀의 범함수(functional)이다.
E₀ = E[⍴₀]
이 경우, N개의 전자를 포함하는 계에 대한 전자 파동 함수
는 모두 3N개의 공간 좌표의 함수이지만, 전자 밀도 ⍴(r→)는 3개의 공간 좌표의 함수이기에 DFT는 전자 구조 계산을 훨씬 더 효율적으로 만들 수 있다.
문제는 에너지를 비롯한 여러 성질에 대한 명확한 범함수(전자 밀도를 변수로 갖는)의 형태를 모른다는 데 있다. 그러나 그간의 연구로 DFT 에너지를 나타내는 여러 항에 대한 개발이 이루어져 계산의 정확도에 큰 진전을 이루어, DFT는 전자 구조 계산을 위한 효과적인 방법으로 주목받고 있다.
현대의 DFT 방법은 하트리-폭 이후 방법에 견줄 수 있는 정확도를 보이면서도 계산 시간을 훨씬 단축해 특히 기존의 하트리-폭 이후 방법을 적용하기 어려운 큰 분자 계에서 널리 사용된다.
화학 동역학[편집]
화학 동역학(chemical dynamics)은 화학 반응과 같이 시간에 따른 분자 계의 동역학적 변화를 다룬다. 전자 구조 계산을 통하여 분자의 퍼텐셜 에너지 표면(potential energy surface)이 결정되면 이 퍼텐셜 에너지 표면에서 시간-의존 슈뢰딩거 방정식(time-dependent Schrödinger equation)을 풀어 화학 반응 과정 동안 원자핵의 운동을 다룰 수 있다.
시간-의존 파동 묶음 동역학(time-dependent wave packet, TDWP) 방법에서는 반응계의 퍼텐셜 에너지 표면에서 초기 상태에 대응하는 파동 묶음(wave packet)으로 시간-의존 슈뢰딩거 방정식을 풀이한다. TDWP 방법은 A + BC 교환 반응의 반응 단면적(reaction cross section)이나 반응성 산란 공명(reactive scattering resonance)을 비롯한 여러 성질을 예측하고, 광들뜸(photoexcitation)과 광해리(photodissociation) 과정의 시간에 따른 동역학적 변화를 묘사하는 데 사용되었다. 특히 펨토 화학(femtochemistry)의 발전은 TDWP 동력학의 시간 의존 접근법을 더욱더 유용하게 하였다.
연구 대상[편집]
양자화학은 그 여명기에 분자구조와 화학결합의 성립에 대해 이론적인 설명과 분자 구조에 기인하는 분광학적 물성의 이해에 중요한 기여를 하였다. 실제 분자를 양자화학으로 이해하는 것은 많은 전자와 원자핵으로부터 구성되는 N입자 문제의 파동 방정식의 해를 구하는 것에 해당한다. 계산화학이 발달하지 않았던 당시에는 양자화학의 학문 영역을 전개하기 위하여 분자 구조 모델을 간소화하는 많고 다양한 근사법이 모색되었다. 또한, 파동방정식의 해를 구하는 것에 있어서도 섭동이론(Perturbation theory)과 변분법(Variational principle)에 따른 근사를 이용하였다. 그러므로, 당시의 양자화학은 정성적인 예측을 하는 데 그쳤지만, 당시까지 설명이 곤란하였던 분광학의 전자 스펙트럼, 진동 스펙트럼, 회전 스펙트럼, NMR 스펙트럼 등의 성질을 분자 구조와 관련지어 공유결합과 분자간 힘의 원리의 설명, HOMO-LUMO 이론으로 대표되는 반(半)정성적인 화학 반응의 이해 등 다른 화학 분야에 있어서 그 공헌이 컸다.
1980년대 이후 급속한 컴퓨터의 처리 속도의 증가와 컴퓨터 공학의 발전은 계산화학으로도 그 파급효과가 이어졌고, 변분법으로부터 발전한 제1원리 계산(Ab initio calculation) 법에 의해 정밀한 해를 구하는 일을 가능하게 하였다. 최근에는 양자 화학에 의해 화학결합과 분자의 미세 구조와의 관련성, 분자간 상호작용과 여기 작용의 설명, 반응의 퍼텐셜 에너지도 간단한 모델화된 분자가 아닌 실제 유기화합물, 착화합물, 고분자, 생체관련물질, 고체표면에서의 계면화학의 해석 등 다양한 화학 분야에 미치고 있다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원