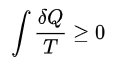열역학
열역학(Thermodynamics, 熱力學)은 에너지, 열, 일, 엔트로피와 과정의 자발성을 다루는 물리학의 분야다. 통계 역학과 밀접한 관계를 가지며 그로부터 수많은 열역학 관계식을 유도할 수 있다. 열역학은 열이 일정량의 기계 작업에 해당하는 에너지의 한 형태로서 이 에너지가 한 곳에서 다른 곳으로 그리고 한 형태에서 다른 형태의 에너지로 전달하는 것을 해석한다.[1] [2][3][4]
목차
개요[편집]
열역학이라는 단어는 열을 뜻하는 'Thermos'와 역학을 나타내는 'Dynamics' 두 단어가 조합되어 만들어졌다. 열역학은 열과 에너지, 일 그리고 이들 간의 상관관계를 다루는 자연과학의 한 분야로 열을 일로 전환하는 효율을 극대화하는데 기여하였으며 열역학의 발달은 산업혁명과 그로 인한 엄청난 사회적 변화의 지적 추진력이 되었다. 물질이나 에너지를 서로 교환하는 여러 물리계 사이의 열역학적 과정을 다룰 때 고전 열역학은 그 과정이 완료되는 시간이나 그 과정이 얼마나 빨리 일어나는지에 대해서는 관심을 갖지 않는다. 열역학이라는 용어 대신 평형 열역학(equilibrium thermodynamics)이란 용어를 사용하며 준정적 과정(quasi-static process)이라는 개념을 사용한다. 준정적 과정은 매우 천천히 변하여 각 순간마다 평형상태로 간주할 수 있는 이상적인 과정을 말한다. 비평형 열역학(non-equilibrium thermodynamics)은 시간에 따라 변화하는 열역학적 과정을 연구한다. 일상생활에서 열역학은 많은 부분에 응용되고 있기 때문에 열역학은 공학의 이해에서 필수적이다. 열역학은 물질의 상태(state) 변화에 따라 발생하는 열(heat)과 일(work)의 양을 열역학 법칙으로 정의되는 에너지와 엔트로피 등의 열역학적 변수들을 이용하여 분석하는 학문이다. 열역학에서는 우주를 열역학적 분석의 대상인 계(system)와 계를 제외한 주위(surroundings)로 나눈다. 계에 대한 열역학적 측정을 수행하는 공간도 주위의 개념에 포함된다.
열역학 법칙은 매우 일반적인 법칙으로 관찰하는 대상이나 물질 사이의 상호작용에 상관없이 항상 성립하는 법칙이다. 즉 관찰하고자 하는 계와 이를 둘러싼 환경 사이에 에너지와 물질 교환이 평형을 이룬다는 사실만 확인되면 항상 적용할 수 있다. 열역학은 18세기 산업혁명 이후 증기기관과 같은 열기관(heat engine)의 작동 원리를 이해하고 효율을 향상시키기 위한 수단으로 활용되기 시작하여 19세기 중엽에 완성되었다. 오늘날 열역학은 화학, 물리학, 생물학, 지질학, 기상학, 해양학, 화학공학 등의 다양한 분야에서 널리 활용되고 있다. 열역학은 열평형에 대한 열역학제0법칙, 에너지의 보존에 대한 열역학제1법칙, 엔트로피의 변화에 대한 열역학제2법칙, 그리고 절대온도 영도에서의 엔트로피에 대한 열역학제3법칙의 네 개의 열역학법칙이 있다. 열역학은 네 개의 법칙으로부터 출발해 다양한 열역학적인 결과를 유도할 수 있다는 면에서 공리체계를 가진 수학적 구조와 흡사하다.
역사[편집]
열역학의 역사는 열과 에너지에 관한 정의라 해도 무관하다. 1789년, 벤자민 럼포드(B. T. Rumford)에 의해 열을 물질의 일종이라 간주했던 열소이론이 깨지면서 열역학의 역사가 시작되었다. 1801년 존 돌턴(John Dalton)은 모든 기체는 온도의 증가에 따라 그 부피가 균일하게 증가한다는 사실을 발견했다. 1808년 게이뤼삭(Joseph Louis Gay-Lussac)은 모든 기체의 부피가 0으로 되는 온도를 외삽에 의해 예측할 수 있게 하였고 -273℃를 절대온도 0이라고 하였다. 1824년 니콜라 레오나르 사디 카르노(Nicolas Léonard Sadi Carnot)가 카르노 사이클을 만들었고, 1849년 켈빈 경에 의해 타당성이 입증되었다. 1850년 루돌프 클라우지우스(Rudolf Julius Emanuel Clausius)는 열역학 제2법칙을 정의하고 몇 달 뒤에 열역학 제1법칙도 정의했다. 1873년 반데르발스(Johannes van der Waals)가 상태방정식을 고안했다. 1878년 조시아 깁스(Josiah Willard Gibbs)는 깁스에너지와 상률의 개념을 도입했다. 1886년 라울(François Marie Raoult)은 프랑코 라울의 법칙을 발표하였고, 1901년 길버트 루이스(Gilbert Lewis)는 퓨개시티와 활동도의 개념을 도입했다. 1949년 레들리히(Otto Redlich)와 쾅(J. N. S. Kwong)은 상태방정식을 실제기체에 맞게 수정하였고 1955년 케네스 피쳐(Kenneth Pitzer)는 비중심 인자(acentric factor, 편심 인자, 이심 인자)의 개념을 도입하여, 실제기체의 압축계수를 구하는 방법을 제시하였다. 흔히 여기까지의 역사를 고전열역학의 범주로 불린다.[5][6]
열역학 변수[편집]
보통 이상기체 상태 방정식과 같은 상태 방정식(equation of state)에 나타나는 변수들을 열역학적 변수라고 부르지만 이 변수들로 표현되는 성질들도 열역학적 변수라고 한다.
- 온도(temperature): 물질의 뜨거운 정도를 나타내는 것으로, 계를 구성하는 분자의 평균 운동에너지에 해당한다. 열역학에서는 '섭씨'나 '화씨' 대신 흔히 T로 나타내는 '절대 온도'(absolute temperature)를 많이 사용한다. 절대 온도의 국제표준(SI)단위는 '켈빈'이고 K로 나타낸다. 절대 온도(T)와 섭씨 온도(t)의 관계식은 T/K = t /°C + 273.15이다.
- 엔트로피(entropy): 계의 무질도를 나타내는 척도로 S로 쓰고, SI 단위는 J/K이다. 고립계에서 상태 변화가 일어나면 엔트로피는 언제나 증가하기 때문에 자발적으로 일어나는 변화의 방향을 설명할 때 사용된다.
- 압력(pressure): 단위 면적에 미치는 힘으로, p로 쓰고, SI 단위는 Pa (= N/m2, 파스칼)이다.
- 부피(volume): 계가 차지하는 공간으로, V로 쓰고, SI 단위는 m3이지만 L(liter)도 많이 사용된다.
- 화학 퍼텐셜(chemical potential): 열역학에서 화학 퍼텐셜은 변화의 방향을 알려주는 물리량이다. 일반적으로 기호는 μ로 쓰고, SI 단위는 J/mol이다.
- 몰(mole): 계에 들어있는 원자 또는 분자의 수를 나타내고, n을 쓰고, SI 단위는 mol이다.
위에 열거된 역학적 변수들은 근본적인 고전 물리학 혹은 양자 물리학으로 기술할 수 있지만, 통계적인 변수는 오로지 통계 역학으로만 이해할 수 있다. 열역학이 적용되는 대부분의 경우에 하나 이상의 열역학 변수는 변하지 않는 상수로 간주되고 나머지 변수들만 변하게 된다. 수학적으로 이것은 계의 상태를 n-차원 공간의 한 점으로 대응시켜 기술할 수 있다. 여기서 n은 상수가 아닌 변수의 개수이다. 통계 역학을 고전 물리학이나 양자 물리학과 결합하여 이들 변수들 사이의 관계식을 나타내는 상태 방정식을 유도할 수 있다.
열역학적 퍼텐셜[편집]
계의 변화 경로와 무관하게 계의 주어진 상태에 고유한 성질로, 열역학적 변수에 포함시키기도 한다.
- 에너지(energy): 열역학 제1법칙에 의해 정의되는 것으로, 계가 주위에 할 수 있는 최대의 일과 열의 양에 해당한다. '내부 에너지'(internal energy)라고 부르기도 하고, U로 쓰고, SI 단위는 J 이다.
- 엔탈피(enthalpy): H = U + pV 로 정의되고, '열함량'(heat content)이라고 부르기도 한다. 일정한 압력에서 일어나는 변화를 설명할 때 유용하게 사용된다.
- 헬름홀츠 에너지(Helmholtz energy): A = U - TS 로 정의되고, 일정한 온도와 부피에서 일어나는 변화를 설명할 때 유용하게 사용된다.
- 깁스 에너지(Gibbs energy): G = H - TS 로 정의되고, 일정한 온도와 압력에서 일어나는 변화를 설명할 때 유용하게 사용된다.
엔트로피와 화학 퍼텐셜도 상태 함수이다.
열역학 계[편집]
열역학 계란 우주 전체 중에서 우리가 관심있는 일부를 말한다. 우주 전체 중에서 우리가 관심갖는 계를 제외한 나머지 우주를 흔히 환경 또는 열원라고 부른다. 환경과 계 사이에 실제 경계 혹은 가상적인 경계가 존재하여 이 둘을 분리할 수 있다. 이 경계의 특성에 따라 환경과 계 사이에 에너지만 이동할 수도 있고, 물질이나 엔트로피도 이동할 수 있다. 따라서 이 경계의 특성에 따라 열역학 계를 분류한다.
계와 환경 사이의 에너지, 물질, 엔트로피 교환형태에 따라 다음과 같이 열역학 계를 3가지로 분류한다.
- 고립계: 환경과 열, 물질, 일 모두 교환하지 않는 계이다. 이 말은 수학적으로 TdS=0,dN=0,pdV=0를 의미하며, 따라서 dE=0를 의미한다. 고립계의 예로, 외부와 완전히 격리된 기체 실린더를 예를 들 수 있다.
- 닫힌계(closed system): 환경과 에너지(열과 일)는 교환하지만 물질은 교환하지 않는 계를 말한다. 일반적으로 닫힌계에서는 오직 {\displaystyle dN=0}{\displaystyle dN=0}이다. 예를 들어, 온실은 온실 외부(환경)과 열을 교환하지만 물질을 교환하지 않으므로 닫힌계로 간주할 수 있다. 계가 열을 교환하든지 혹은 일을 교환하든지 혹은 둘 다 교환하든지, 이런 특성은 경계의 성질로 이해하여 다음과 같은 경계를 정의한다.
- 단열 경계(adiabatic boundary): 열교환이 일어나지 않는다. TdS=0
- 단단한 경계(rigid boundary): 일 교환이 일어나지 않는다. pdV=0
- 열린 계(open system) : 에너지(열과 일), 물질 모두 환경과 교환하는 계이다. 이런 경계는 투과성 있는(permeable) 경계라 한다. 바다는 열린 계로 간주할 수 있다.
현실적으로 환경으로부터 완전히 분리된 엄밀한 고립계는 존재할 수 없다. 왜냐하면 아무리 환경과 계 사이의 결합을 제거하더라도 중력은 제거할 수 없기 때문이다. 정상상태의 계에서 빠져나가는 에너지와 들어오는 에너지는 같다. 주어진 일련의 조건 하에서 평형상태의 계는 정의된 상태(definite state)라고 한다. 계의 상태는 여러 세기 변수(intensive variables)와 크기 변수(extensive variables)로 기술된다. 계의 특성은 이 변수들 사이의 관계를 정해주는 상태 방정식(equation of state)로 기술된다.
열역학 법칙[편집]
열역학에는 네 가지의 근본적인 법칙이 있다. 이 사법칙은 여러 가지의 서로 동등한 방법으로 기술할 수 있다.
열역학 제0법칙: 열적 평형의 추이성[편집]
열역학 제 0 법칙에 따르면, 만약 계 A와 계 B가 접촉하여 열역학적 평형상태를 이루고 있고 계 B와 계 C가 접촉하여 열역학적 평형상태를 이루고 있다면, 계 A와 계 C가 접촉하여도 열역학적 평형을 이룬다. 두 계가 접촉하였을 때 열역학적 평형을 이루지 못한다면, 두 계 사이에 에너지나 물질의 알짜이동이 있다. 서로 열역학적 평형을 이루고 있는 두 계는 나중에 다시 접촉하였을 때도 평형을 이룬다.
열역학 제0법칙은 열역학의 근본적인 개념이지만, 이것을 법칙으로 진술하게 된 것은 놀랍게도 열역학의 많은 부분이 완성된 후인 1930년대이다. 이미 열역학 1,2,3법칙이 확립되었기 때문에, 열역학의 가장 근본적인 이 개념은 자연스럽게 0법칙의 지위를 얻게 되었다. 여전히 열역학 제0법칙의 지위에 대한 논의가 이루어지고 있다.
열역학적 평형은 열적 평형(열교환과 온도와 관계)과 역학적 평형(일교환과 압력 같은 일반화된 힘과 관계)과 화학적 평형(물질교환과 화학퍼텐셜과 관계)을 포함한다.
요약: A와 B가 열평형을 이루고 있고, B와 C가 열평형을 이루고 있다면, A와 C도 서로 열평형을 이룬다.
열역학 제1법칙: 에너지 보존[편집]
열역학 제 1 법칙에 따르면, 단열 과정에서 일교환은 과정(process)의 구체적인 형태에 상관없이 초기 상태와 최종 상태에만 관계한다. 단열과정에서는 열이동이 없기 때문에, 이것은 에너지 보존 법칙과 동등한 진술이다. 이 법칙은 단열과정하에서 계의 에너지 이동은 계가 한 일 혹은 계에 한 일밖에 없음을 의미한다. 이는 수학적으로 다음과 같이 표현된다.
여기서 U는 계의 내부 에너지, q는 계로 흘러들어간 열에너지, w는 계가 한 일이다.
- 열전도율(P)
고온의 열저장고와 저온의 열저장고를 물체로 연결해놓으면 고온의 열저장고에서 열에너지가 저온의 열저장고로 전도된다. 이러한 전달되는 열에너지를 단위시간당 전달되는 비율을 전도율이라고 한다. 연결된 물체의 면적을 A, 길이를 L이라고 하면 전도율 P = kA(Th-Tc)/L로 나타낼 수 있다(k=열전도도, Th=고온의 열저장고의 온도, Tc=저온의 열저장고의 온도). 열전도도 k 는 물체의 고유한 특징으로 상수값을 지닌다. 열에너지를 빨리 전달하는 물질일수록 좋은 열전도체로서 k값이 크다.
요약: 고립계의 에너지총합은 일정하다
열역학 제2법칙: 엔트로피의 증가[편집]
열역학 제2법칙에 따르면, "열원(reservoir)으로부터 양의 열에너지를 뽑아서 모두 일로 전환하되, 다른 추가적인 효과를 동반하지 않는 순환과정(cycle)은 존재하지 않는다."(Kelvin-Planck 진술) 다시 말해, 열적으로 고립된 거시계의 엔트로피는 절대 감소하지 않는다. 하지만 미시계에서는 제2법칙이 진술하는 것과 반대로 행동하는 엔트로피의 요동(fluctuation)이 있다. 사실, 가역 동역학(time-reversible dynamics)와 인과율의 공리(Axiom of Causality)로부터 요동 정리를 수학적으로 증명할 수 있고, 이것이 제2법칙의 증명이 되겠다. 논리적으로 제2법칙은 물리학의 "법칙"이라기 보다, 매우 큰 계 혹은 오랜 시간에 대한 정리일 뿐이다.
요약: 고립계에서의 엔트로피는 절대 감소하지 않는다.
열역학 제3법칙: 절대 0도의 불가능성[편집]
열역학 제3법칙은 통계학상으로 나타나는 자연적인 법칙이며, 절대영도에 다다르는 것의 불가능에 대하여 다룬다. 이 법칙은 엔트로피의 값의 결정에 기준점(절대영도)을 제공해 주는데, 이처럼 절대영도를 기준으로 하여 상대적으로 결정된 엔트로피를 절대 엔트로피라고 한다.
엔트로피는 절대영도에 가까워질수록 변화량이 0에 수렴하며, 절대영도에서 완전한 결정상태의 엔트로피는 0이다. 다만 자연계에서 절대영도는 존재할 수 없고 단지 0으로 수렴할 뿐이다.
'어떠한 계, 혹은 계의 어떠한 상태에서든지, 엔트로피는 절대영도에서 최소이다'라고 표현할 수도 있으며, '유한번의 과정을 통해 절대영도에 도달하는 것은 불가능하다'라는 표현도 사용할 수 있다.
요약: 자연계에서 절대영도는 존재하지 않는다.[7]
각주[편집]
참고자료[편집]
- 〈열역학〉, 《위키백과》
- 〈열역학 법칙〉, 《위키백과》
- 〈열역학〉, 《나무위키》
- 〈열역학〉, 《네이버 지식백과》
- "Thermodynamics", Wikipedia
- 캘빈경, 〈열역학의 역사〉, 《네이버 블로그》, 2018-09-02
- Sortie, 〈(Thermodynamics) 01. 열역학의 역사〉, 《네이버 블로그》, 2021-09-04
같이 보기[편집]

 위키원
위키원