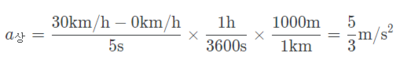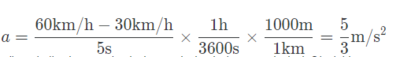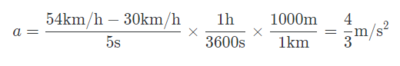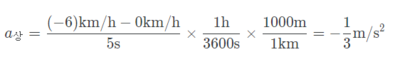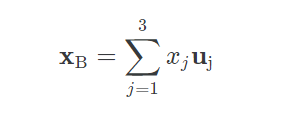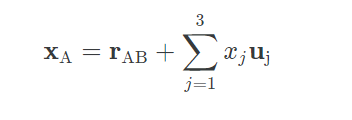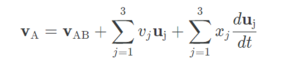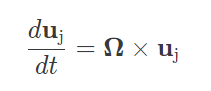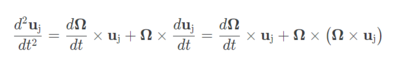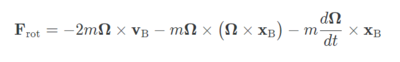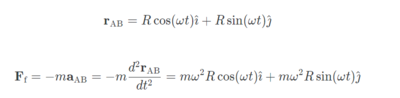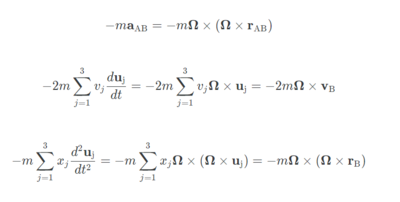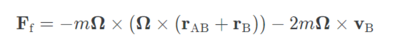관성력
관성력(慣性力, Inertial force)은 비관성 기준틀에서 물체의 운동을 기술할 때 도입되어야 하는 힘으로 실재하지 않는 가상적인 힘이다. 관성력은 겉보기 힘(fictitious force), 유사 힘(pseudo force), 혹은 달랑베르 힘(d'Alembert force)이라고 불리기도 한다. 관성력은 물체 사이의 물리적 상호작용에서 기인하는 것이 아니라 비관성 기준틀 자체의 가속에서 기인한다.
관성력은 물체의 운동을 기술하는 기준틀이 관성 기준틀에 대해 가속할 때 나타난다. 기준틀의 가속은 임의의 방법으로 가능하므로, 관성력도 임의적인 양상을 띤다. 하지만 통상적인 예들에서 나타나는 관성력은 네 가지 종류가 있다. 즉, 기준틀이 직선적으로 가속될 때의 관성력과, 회전 가속틀에서 나타나는 두 가지의 힘인 원심력과 코리올리힘(Coriolis force), 그리고 회전율이 시간에 따라 변할 때 나타나는 오일러 힘(Euler force)이 그것들이다. 그리고 일반 상대론에서는 중력도 관성력으로 간주된다.
목차
개요[편집]
관성력은 관성의 법칙에 따라 물체는 운동 상태를 유지하려는 성질을 나타낸다.
속도를 지니고 운동하는 물체를 멈추거나 멈춰 있는 물체에 외력을 가해서 운동시킬 경우 관성의 법칙에 따라 물체는 운동 상태를 유지하려는 성질을 나타내며 그에 따라 외력과 반대 방향으로 작용하는 힘이 존재하는 것처럼, 즉 저항력이 존재하는 것과 같이 느껴지기 때문에 이를 관성력이라 하며 저항력이란 의미로 관성저항이라 부르기도 한다.
또한 운동 제3법칙에 따라 관성에 의해 작용하는 반작용력을 의미하기도 하며, 두 경우 모두 저항력의 크기는 같지만, 작용의 기준이 되는 물체의 관점이 다른 점에 따른 구분으로 볼 수 있다. 원심력이나 코리올리의 힘은 관성력의 하나이다.
본론[편집]
상대 가속도[편집]
30km/h로 운전하는 차에 타 직선도로를 따라 드라이브 하면서 바깥 풍경을 관찰하고 있다고 생각해보자. 아름다운 풍경에 감탄하며 자신이 차를 타고있다는것을 다 잊어버리고 무의식에 맡겨놨다고 생각하자. 그렇다면 일정 간격마다 가로수로 심어진 단풍나무는 (사실 가만히 있지만) 30km/h로 뒤로 가는것 처럼 느껴질것이다. 이것이 모두가 잘 아는 상대속도이다. 그런데 30km/h의 느린 운전에 짜증을 낸 뒷 차가 5초 동안 60km/h까지 등가속하여 추월을 하기 시작했다. 상대속도의 관점에서 뒷차의 가속도를 구해보면, 0km/h의 상대속도에서 30km/h의 상대속도까지 가속운동을 5초동안 하였으므로 "상대" 가속도는
가 된다.
뒷차의 상대 가속도에 의한 뉴턴의 운동 제2법칙[편집]
이야기의 내막을 알고있는 우리의 입장에서 가속도와 알짜힘을 다시 한 번 구해보자. 뒷 차는 30km/h에서 60km/h로 5초동안 가속운동하였으므로 가속도는
상대 가속도와 같다. 그러면 질량은 불변이니 알짜힘은 2500N.
뒷차의 입장에서 앞 차를 이해하기[편집]
뒷차의 입장에서 보는 앞차는 0km/h에서 -30km/h로 5초동안 가속한다. 위와 유사한 계산은 생략하고 부호만 바뀌었으니 상대 가속도는 -5/3m/s² 이다. 앞차의 질량을 1200kg라고 한다면, 알짜힘은 -2000N.
전지적 시점에서 바라본 앞차[편집]
앞차의 실제 가속도는 0이고 알짜힘도 0이다.
겉보기 힘[편집]
전지적 관점과 상대적 관점에서 바라본 앞차의 알짜힘의 차이는 어디서 나온것일까.
알짜힘 앞 차 뒷 차 전지적 0 2500N 상대적 -2000N 2500N
그것은 관찰자가 탑승한 차(=기준계)의 운동상태와 관련있다. 등속운동을 하고있는 앞차(=관성 기준계)의 운전자는 자신이 운동하고 있다는 사실을 아는지 모르는지와는 상관없이 자신이 관찰하고 있는 대상인 뒷차의 알짜힘을 아무런 "편견"없이 파악할 수 있는것이다. 그런데 뒷차의 운전자는, 자신의 자동차(=비관성 기준계)가 2500N의 힘을 받으며 가속운동을 하고있다는 사실을 잊어버린다면, 마치 앞차가 반대방향으로 2000N만큼 힘을 받고 있다고 거꾸로 생각하게 되는것이다. 즉, 관찰자인 뒷차의 운전자가 착각하고있는 앞차의 알짜힘 -2000N이 바로 관성력이고, 이것은 사실 (관찰대상인 앞차가 아니라) 뒷차의 운전자 자신의 가속도(5/3m/s²)에 앞차의 질량(1200kg)을 곱해주고 부호만 바꾼것이다.
만약 뒷차의 운동은 그대로이고, 앞차가 30km/h에서 54km/h까지 5초간 등가속운동을 한다면 어떻게 될까? 앞차의 가속도는
이고, 상대가속도는
이 되어, 가속도로 계산한 알짜힘은 1600N, 상대가속도로 계산한 알짜힘은 -400N이 된다. 또한 앞차가 바라본 뒷차의 상대가속도는 뒷차가 바라본 앞차의 상대가속도와 부호만 다르므로, 쉽게 계산할 수 있다.
알짜힘 앞 차 뒷 차 전지적 1600 2500N 상대적 -400N 500N
위 표에서 뒷차의 운전자가 바라본 앞차의 상대적인 알짜힘 -400N은 앞차에 실제로 적용 알짜힘인 1600N에 뒷차의 가속도 5/3m/s²에 앞차의 질량 1200kg을 곱해준 값 2000N을 빼준 값이다. 이를 일반화하면, 가속운동하는 공간안에 있는 관찰자가 어떤 물체에 적용된 알짜힘에 대해 관찰 할 때, 다음과 같이 관찰한다고 볼 수 있다.
위 식에서 -ma공간는 물체에 실제로 적용된 힘은 아니지만, 관찰자는 실제로 적용된 알짜힘에 -ma공간을 더한 값을 관찰하게 되고, 이 -ma공간을 관성력 또는 겉보기 힘이라고 한다.
심화[편집]
관성력 방정식[편집]
먼저 가만히 있는 관측자 A, 이리저리 움직이고 회전하는 B, 그리고 입자가 하나 있다고 가정해보자. B의 관점에서 입자의 위치를 XB 라 하자. 또한, B의 좌표의 단위벡터를 u₁, u₂, u₃ 라 하자. 마지막으로, A에서 B로 향하는 벡터를 rAB 이라 하자. 그렇다면,
따라서 A의 관점에서 입자의 위치는 다음과 같다.
양변을 시간에 대해 미분하자. 맨 오른쪽 항에는 곱의 미분법을 적용한다.
이건 속도다. 한번 더 미분해서 가속도를 얻자. 이번에는 두 항에 곱의 미분법을 적용한다.
중간에 두 항은 동일하니 같이 묶으면
뉴턴의 제2 법칙은 F = ma
이걸 이전 공식에 적용하자. 양변을 입자의 질량인 m으로 곱해주면 된다.
여기서 FA 는 A가 생각하는 입자에게 가해지는 힘이고, FB 는 B가 생각하기에 입자에 가해지는 힘이다. 하지만,
FB = FA + 관성력
이니까 관성력 (Ff)은 다음과 같다.
회전[편집]
전 문단에서 구한 방정식 중에서 2번째와 3번째항이 회전할 때 발현된다. 회전을 하면 좌표의 단위벡터들의 방향이 바뀌기 때문이다. 먼저, 회전 벡터 Ω를 정의하자. 이 벡터의 방향은 오른손의 법칙으로 정의되며, 절댓값은 회전하는 B의 각속도다.
단위 벡터들은 이 회전벡터의 방향과 수직으로 변화하므로,
이 식이 왜 성립하냐 더 따져보자. 단위벡터와 회전벡터 사이의 각도를 ϕ라 하자. 단위벡터는 Ω를 축으로 원 운동을 할 것이다. 이 원의 반지름은 u sin ϕ다. 아주 작은 시간 단위 Δt가 지난뒤, 단위벡터의 끝이 이동한 "거리"는 Δu/Δt ∙ Δt = (usinϕ)(ΩΔt)→ Δu/Δt = Ωu sin ϕ. 이는 호의 길의가 Rθ이기 때문이다. 여기서 RR이 u sin ϕ, θ가 ΩΔt. 그러므로 |du/dt| = ∣Ω×u∣. 변화하는 방향도 이 외적과 일치하니 (오른손 법칙으로 쉽게 확인 가능), du/dt =Ω×u가 성립한다.
양변을 한번 더 미분하면
duj/dt와 d²uj/dt²를 3.1문단의 방정식에 대입하면, 회전으로 인한 관성력은 다음과 같다. 단, B는 회전만 할 뿐 다른 가속은 하지 않는다고 가정.
첫번째 항이 코리올리 힘, 두번째 항이 원심력, 세번째 항은 오일러 힘이다.
공전[편집]
회전 없는 공전을 보자. 단, 공전의 각속력(ω)은 일정하다고 가정하고, 공전의 반지름은 R. du/dt=0 이니 −maAB 만 신경쓰면 돼서, 계산이 매우 간단하다. x-y평면을 공전의 평면으로 잡으면 계산은 더더욱 쉬워진다.
이 결과는 3.2에서 본 원심력과 비슷한데, 가장 중요한 차이점은 공전하는 관점에서 원심력은 위치에 따라 그 크기가 변하지 않는다. 반면 자전하는 관점에서의 원심력은 회전축으로부터 멀어질 수록 크기가 증가한다.
공전과 동시에 회전: 조석고정[편집]
현실에서도 매우 흔하게 찾아볼 수 있는 현상. 굳이 지구-달 같은 조석고정이 된 계가 아니어도 뭔가를 줄으로 꽉 매달고 빙빙 돌리거나, 원심 분리기를 사용하거나 할 때도 적용이 가능하다. 심지어 인간이 원형 트랙에서 달리는 것도 수학적으로 동일한 상황이다 (항상 시야의 왼쪽 또는 오른쪽이 항상 원의 중심을 향하고 있으므로). 이런 가정을 하면 공전의 회전벡터와 자전의 회전벡터가 Ω로 완전히 동일하다. 마지막으로, Ω는 항상 일정하다고 가정한다.
그러니까 관성력은
첫번째 항이 일종의 합동 원심력이고, 두번째 항이 코리올리 힘.
관성과 관성력의 차이와 오해[편집]
고전물리 학습자가 관성과 관성력에 관하여 처음으로 마주치는 예시는 출발 하는 버스의 문제일 것이다. 정지해있던 버스가 출발할 경우 서 있던 승객은 관성력이 작용하여 뒤로 넘어지려는 힘(=관성력)을 느낀다는것이 바로 그것이다. 여기서 첫번째 오해가 생기는데, 관성력이 실제로 작용하는 힘이라고 생각해버리는 것이다. 그러나 이 승객이 실제로 받는 힘은 자신의 발바닥에 가하는 버스 바닥의 정지 마찰력이다. 또한 이 힘의 방향은 승객이 넘어지려는 방향이 아닌 버스가 가속하는 방향이다. 두번째 오해는 관성력이 관성을 유지해주는 힘이라는 것이다. 그러나 뉴턴은 자신의 첫 번째 운동법칙에서 '관성'이라는 단어 자체를 "외부의 힘이 '없을 때' 등속운동을 한다는 것"으로 정의하였다. 다시 말하면 알짜힘이 존재하면 관성이라는 상태는 있을 수 조차 없다.
관성력의 예[편집]
- 가속하는 버스의 손잡이가 가속방향의 반대로 기울어지거나 사람이 넘어지는 현상
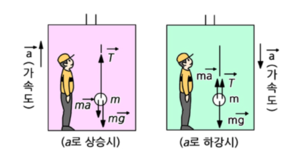
- 엘리베이터를 타고 오르내리면서 느끼는 무거워지거나 가벼워진다고 느끼는 현상
- 우주 정거장에서 중력을 느끼는 현상
참고자료[편집]
같이 보기[편집]

 위키원
위키원