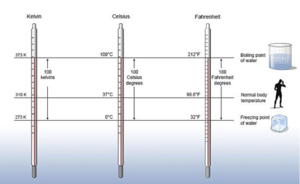
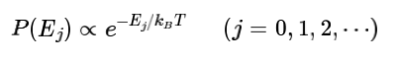온도(temperature)는 물체의 차갑고 뜨거운 정도를 나타내는 물리량이다. 온도의 SI 기본 단위는 K(켈빈)이지만, 일상생활에서는 ℃(섭씨)나 °F(화씨)를 주로 사용한다. 영국의 켈빈 경(윌리엄 톰슨)의 이름을 딴 켈빈 온도(K)는 열역학에서 쓰인 절대온도 단위로, 절대 0도(0K)는 고전 열역학적인 의미에서 계의 모든 열적 운동이 멈추는 온도이다.
SI 단위에서는 2018년까지 물의 3중점을 273.16K로 정의하였지만, 2019년 5월부터 볼츠만 상수를 정확히 1.380649× 10⁻²³J ∙ K⁻¹로 정할 때 정의된 온도로 켈빈 온도를 정의한다.
스웨덴 과학자 안데르스 셀시우스의 이름을 딴 섭씨온도 역시 SI 유도 단위이고, 현재 미국, 바하마, 벨리제, 케이먼 군도, 리비아를 제외한 전 세계 모든 나라에서 사용하고 있다. 섭씨온도는 1기압에서 물의 어는점을 0℃로, 물의 끓는점을 100℃로 정하여 만들어진 온도이다. 화씨 온도(°F)는 1724년 네덜란드-독일-폴란드 물리학자인 파렌하이트(Fahrenheit)가 처음 제안하였다. 초기에 화씨온도는 동일한 양의 얼음, 물, 염화암모늄으로 이루어진 염용액의 어는점을 0°F로 정의하였다. 나중에는 얼음의 녹는점을 32°F 로, 인간의 체온을 96°F로 정의하여 사용하였다. 현재의 화씨온도는 1기압에서 물의 어는점을 32°F로, 물의 끓는점을 212°F로 정하여 만들어진 온도이다. 화씨온도는 현재 미국, 팔라우, 미크로네시아, 마셜 군도, 바하마, 케이맨 군도, 리비아 등에서만 사용하고 있다.
온도는 물질의 뜨겁고 찬 정도를 나타내는 물리량이다. 온도는 물리학에서 가장 기초적이고 중요한 물리량 중 하나이다. 온도는 일반적으로 다음 두 가지 방법으로 정의된다.
일반적인 정의의 온도는 온도의 경험적인 개념과, 독립적인 온도의 존재성을 보장하는 열역학 법칙중 제 0법칙에 기초한다. 일반적인 정의의 온도는 온도의 기준을 통해 만들어진 온도계로 측정되는 값이다.
열역학적 정의의 온도는 19세기 중반 열기관과 열역학에서 이어지는 통계역학이 발전되면서 에너지와 엔트로피간의 이해가 높아지면서 파생되어 나왔다. 열역학적 정의의 온도는 에너지를 엔트로피로 편미분한 값으로 나타내지며, 다양한 기초적인 물리법칙과 근본적으로 관련되어있다. 열역학적 정의의 온도는 계의 평형이 이뤄지지 않으면 정의할 수 없다.)
온도의 국제 단위는 켈빈(K)이다. 켈빈은 물의 삼중점의 열역학적 온도의 1/273.16으로 정의된다. 일반적인 정의에 사용되는 온도 기준에 열역학적 정의의 온도를 사용함으로써 일반적인 정의의 온도라도 물리학적인 의미, 다양한 기초적인 물리법칙과의 관련성을 만들 수 있다.
온도 단위 간의 관계[편집]
섭씨온도와 켈빈 온도의 관계는 다음과 같다. 예를 들면, 25℃는 298.15K와 같다.
K = ℃ + 273.15
섭씨온도와 화씨온도의 관계는 다음과 같다. 예를 들면, 25℃는 77°F와 같다.
°F = ℃ × 9/5 +32
열학에서의 온도[편집]
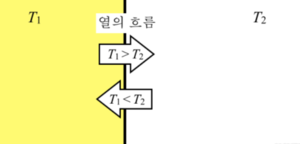
열역학에서 온도는 열의 형태로 에너지가 자발적으로 전달되는 방향을 결정하는 인자이다. 예를 들면, 온도가 다른 두 물체가 서로 맞닿아 있다면 온도가 높은 물체에서 온도가 낮은 물체로 열이 전달된다. 이를 열역학적 온도라고 한다. 열역학적 온도 T의 단위는 K(켈빈)으로, T=0이 가장 낮은 온도 (절대 0도)이다.
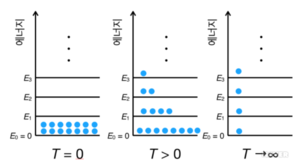
통계 열역학에서 온도는 계의 확률 분포를 결정한다. 예를 들면, 정준 앙상블(canonical ensemble)에서 계가 에너지 상태 Ej(E₀=0 ≤E₁≤ E₂≤...)를 가질 확률(P(Ej))은 다음과 같이 볼츠만 인자(Boltzmann factor)에 비례한다.
여기서 KB는 볼츠만 상수이다. 만약 T=0이라면, Ej>0인 에너지를 갖는 계는 존재하지 않는다. 즉, 모든 계는 바닥 상태 (Ej=0)에 존재한다. 반대로 T → ∞이라면, 와 상관없이 모든 계가 존재할 확률은 같다. 그렇다면 유한한 온도에서 에너지 상태에 따른 계의 분포는 어떻게 될까? 에너지가 낮은 계가 존재할 확률이 지수적으로 증가한다. 이를 볼츠만 분포라고 한다. 이러한 계의 확률 분포와 온도의 관계로부터 음의 절대 온도 개념이 나온다. 계의 확률 분포가 역전되는 시스템, 즉 에너지가 높은 계가 존재할 확률이 지수적으로 증가하는 시스템 온도는 0보다 작다. 즉, 절대 온도가 음이다. 이러한 개념을 실험적으로 선보인 연구가 최근에 등장하였다.
동역학 이론에서의 온도[편집]
동역학 이론 중 하나인 등분배 이론(equipartition theorem)에 의하면 열역학 조건(또는 높은 온도)에서 자유롭게 움직이는 분자의 자유도 (예를 들면, 3차원 자유 입자의 경우 x-방향, y-방향, z-방향 등 총 3개 자유도를 가짐)마다 평균적으로 kBT/2만큼 에너지가 분배된다. 즉, 자유롭게 움직이는 단원자 분자의 경우 3kBT/2의 평균 병진 운동 에너지를 갖는다. 분자의 경우 회전 운동과 진동 운동도 존재하므로 각 운동에 에너지가 분배된다. 선형 분자의 경우 2kBT, 비선형 분자의 경우 3kBT/2의 회전 운동 에너지를 갖는다. 진동 운동에 분배되는 에너지는 좀 더 복잡하다
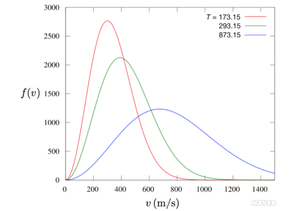
기체의 속도 분포 역시 온도와 연관되어 있다. 자유롭게 움직이는 기체의 속력 분포 [f(v)]는 맥스웰-볼츠만 분포(Maxwell-Boltzmann distribution)로 표현할 수 있다.
여기서 M과 R은 각각 기체의 분자량과 기체 상수이다.
위 그림에서 알 수 있듯이, 온도가 높아질수록 속력 분포가 더 넓어지고, 평균 속력 또한 커진다(Vmean ∝ √T).
참고자료[편집]
- 〈온도〉, 《화학백과》
- 〈온도〉, 《위키백과》
같이 보기[편집]
|
  이 온도 문서는 자연에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요. 이 온도 문서는 자연에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.
|
| 일반 : 자연 □■⊕, 생물, 동물, 식물, 정치, 군사, 경제, 사회, 교육, 문화, 예술, 스포츠, 역사, 역사인물, 인간, 인체, 건강, 정신, 성격, 행동, 언어, 수학, 위키 도움말
|
|
|
| 우주
|
1차원 • 2차원 • 3차원 • 4차원 • 5차원 • 11차원 • 공전 • 광년 • 광속 • 금성 • 다중우주 • 달 • 목성 • 별 • 보이드 • 블랙홀 • 빅뱅 • 빛 • 세계 • 세상 • 소행성 • 수성 • 안드로메다 은하 • 암흑물질 • 암흑에너지 • 우주 • 우주배경복사 • 위성 • 은하 • 은하계 • 은하단 • 자전 • 중력파 • 중성자별 • 지구 • 지축 • 진공 • 진공에너지 • 차원 • 천문 • 천문학 • 천왕성 • 천체 • 초신성 • 초은하단 • 카오스 • 코스모스 • 태양 • 태양계 • 테라포밍 • 토성 • 펄사 • 편광 • 평행우주 • 항성 • 해왕성 • 행성 • 혜성 • 화성 • 흑점
|
|
|
| 물리
|
가속도 • 관성 • 구심력 • 나노 • 대상 • 막 • 물리 • 물리량 • 물리학 • 물체 • 반응 • 반작용 • 법칙 • 벡터 • 보손 • 상호작용 • 생성 • 소멸 • 속도 • 수직항력 • 스칼라 • 스핀 • 양자 • 양자역학 • 엔트로피 • 역학 • 운동 • 원심력 • 위치 • 유속 • 유체 • 이동 • 일 • 작용 • 정지 • 존재 • 중력 • 중첩 • 초끈 • 초끈이론 • 파동 • 페르미온 • 현상 • 힘
|
|
|
| 물질
|
가스 • 개체 • 고체 • 기체 • 기화 • 농도 • 대상 • 무기물 • 물질 • 밀도 • 반물질 • 부피 • 분자 • 사물 • 상태 • 속성 • 수분 • 습기 • 습도 • 승화 • 압력 • 액체 • 액화 • 온도 • 용융 • 용해 • 원자 • 유기물 • 응고 • 입자 • 전자 • 점도 • 점성 • 증발 • 질량 • 플라즈마 • 플로케 • 함량 • 혼합물
|
|
|
| 자연
|
가뭄 • 가을 • 강 • 강수 • 강우 • 건기 • 겨울 • 계절 • 고기압 • 공기 • 구름 • 그림자 • 기압 • 기온 • 기후 • 날씨 • 낮 • 눈 • 대기 • 대기권 • 더위 • 돌 • 땅 • 모래 • 무지개 • 물 • 물결 • 밀물 • 바다 • 바람 • 바위 • 밤 • 번개 • 봄 • 불 • 비 • 빗물 • 사막 • 산 • 새벽 • 서리 • 소나기 • 소리 • 썰물 • 아침 • 안개 • 암석 • 어둠 • 얼음 • 여름 • 우기 • 우박 • 월식 • 일식 • 자갈 • 자연 • 자연계 • 자연환경 • 장마 • 저기압 • 저녁 • 점심 • 조류 • 조수 • 지진 • 천둥 • 추위 • 태풍 • 토양 • 파도 • 폭우 • 폭풍 • 하늘 • 해 • 햇빛 • 홍수 • 흙
|
|
|
| 시간
|
과거 • 광속 • 그제(그저께) • 글피 • 날 • 내년 • 내일 • 내후년 • 년 • 뉴턴역학 • 다음달 • 달 • 달력 • 때 • 모래시계 • 모레 • 물시계 • 미래 • 분 • 불시계 • 빅뱅 • 상대성이론 • 생체시계 • 세기 • 세슘 • 세월 • 손목시계 • 스마트워치 • 시 • 시각 • 시간 • 시간여행 • 시계 • 시공간 • 시기 • 시절 • 시점 • 아침 • 야간 • 어제 • 엊그제 • 엔트로피 • 연간 • 오늘 • 올해(금년) • 요일 • 원자시계 • 월 • 월간 • 월말 • 월중 • 월초 • 이번달 • 일 • 일간 • 작년 • 재작년 • 저녁 • 점심 • 주 • 주간 (1주일) • 주간 (낮) • 주말 • 주중 • 주초 • 지금 • 지난달 • 진자시계 • 초 • 해 • 해시계 • 핵시계 • 현재
|
|
|
| 공간
|
가로 • 거기 • 거리 • 곡선 • 공간 • 구 • 그곳 • 길이 • 깊이 • 남동 • 남북 • 남서 • 남쪽 • 넓이 • 높이 • 동그라미 • 동남 • 동북 • 동서 • 동서남북 • 동쪽 • 뒤 • 뒷쪽 • 면 • 면적 • 무게 • 반시계방향 • 방향 • 부피 • 북동 • 북서 • 북쪽 • 사방 • 사선 • 상하 • 서남 • 서북 • 서쪽 • 선 • 세로 • 수직 • 수평 • 시계방향 • 쌍곡선 • 아래 • 아래쪽 • 아랫면 • 앞 • 앞쪽 • 여기 • 여기저기 • 옆 • 옆면 • 옆쪽 • 오른쪽(우측) • 왼쪽(좌측) • 원 • 위 • 윗면 • 위쪽 • 이곳 • 이곳저곳 • 입체 • 저곳 • 저기 • 전후 • 점 • 좌우 • 좌우측 • 좌표 • 중간 • 중심 • 중앙 • 직선 • 쪽 • 크기 • 타원 • 팔방 • 평면 • 포물선
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|
| 산업 : 산업, 산업혁명, 기술, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지 □■⊕, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지
|
|
|
| 에너지
|
SMR • 가속운동 • 가시광선 • 가열 • 각속도 • 감마선 • 감속운동 • 강력 • 고압 • 고온 • 고전역학 • 관성력 • 관성모멘트 • 광선 • 광속 • 광전자 • 광전효과 • 광합성 • 기압 • 냉각 • 냉방 • 뉴턴 • 대류 • 대체에너지 • 동력 • 동력원 • 라디오파 • 마이크로파 • 마찰 • 마찰계수 • 마찰력 • 마찰에너지 • 만유인력 • 만유인력의 법칙 • 무중력 • 물리에너지 • 바이오에너지 • 발열 • 발열반응 • 발화 • 방사선 • 방열 • 베타선 • 복사 • 복사선 • 복사에너지 • 부력 • 불 • 블루에너지 • 빛 • 빛에너지 • 삼투압 • 생물에너지 • 석유에너지 • 석탄에너지 • 섭씨 • 소리에너지 • 소수력 • 속력 • 수력 • 수력에너지 • 수소에너지 • 수압 • 수열 • 수열에너지 • 수직항력 • 신생에너지 • 신에너지 • 신재생 • 신재생에너지 • 알짜힘(합력) • 알파선 • 압력 • 압축응력 • 약력 • 양극선 • 양자역학 • 에너지 • 에너지밀도 • 에너지보존법칙 • 에너지원 • 에너지 효율 • 엑스선 • 엔트로피 • 역반응 • 역파장 • 역학적 에너지(기계에너지) • 열 • 열대류 • 열량 • 열복사 • 열분해 • 열에너지 • 열역학 • 열전도 • 열전도도 • 열전도율 • 열절연 • 열팽창 • 열팽창계수 • 열효율 • 온도 • 온도차 • 왕복에너지 • 왕복운동 • 운동에너지 • 원운동 • 원자력 • 원자력에너지 • 위치에너지 • 음극선 • 응력 • 인공태양 • 인장응력 • 인화 • 입자선 • 자외선 • 자유낙하 • 작용 • 재가열 • 재생에너지 • 저온 • 저압 • 적외선 • 전기에너지 • 전도 • 전자기력 • 절대온도 • 정반응 • 정지에너지 • 조력 • 조력에너지 • 조류에너지 • 줄 • 줄의 법칙 • 중력 • 중력에너지 • 지열 • 지열에너지 • 직사광선 • 직선운동 • 진동 • 진동에너지 • 진자 • 진자운동 • 천연에너지 • 청정에너지 • 친환경에너지 • 칼로리 • 탄성 • 탄성에너지 • 태양 • 태양광 • 태양광에너지 • 태양에너지 • 태양열 • 태양열에너지 • 텐서 • 파동 • 파력 • 파력에너지 • 파워 • 파장 • 폐기물에너지 • 폭발 • 풍력 • 풍력에너지 • 풍압 • 항력(드래그포스) • 해양에너지 • 핵반응 • 핵분열 • 핵분열에너지 • 핵붕괴 • 핵에너지 • 핵융합 • 핵융합에너지 • 화력 • 화씨 • 화학 • 화학에너지 • 회전 • 회전수 • 회전에너지 • 회전운동 • 흡열 • 흡열반응 • 힘
|
|
|
| 발전
|
교류발전기 • 마이크로 수력발전 • 물레방아 • 박테리아 발전소 • 발전 • 발전기 • 발전소 • 발전효율 • 변전소 • 비상발전기 • 소수력발전 • 소수력발전소 • 소형모듈원전(SMR) • 수력발전 • 수력발전소 • 원자력발전 • 원자력발전소 • 조력발전 • 조력발전소 • 조류발전 • 조류발전소 • 지열난방 • 지열발전 • 지열발전소 • 직류발전기 • 태양광발전 • 태양광발전소 • 태양광패널 • 태양열발전 • 태양열발전소 • 파력발전 • 파력발전소 • 풍력발전 • 풍력발전소 • 풍차 • 해양 온도차 발전 • 핵융합발전 • 핵융합발전소 • 화력발전 • 화력발전소 • 회전축
|
|
|
| 연료
|
CNG • LNG • LPG • 가스 • 가스충전소 • 가연성 • 갈탄 • 개질수소 • 경유(디젤) • 경질유 • 고급휘발유 • 고압가스 • 고체연료 • 그레이수소 • 그린수소 • 기체연료 • 나무 • 난방연료 • 두바이유 • 등유 • 땔감 • 면세유 • 무연탄 • 무연휘발유 • 바이오 • 바이오가스 • 바이오디젤 • 바이오매스 • 바이오에탄올 • 바이오연료 • 방사성물질 • 배기가스 • 배출가스 • 번개탄 • 부생수소 • 분별증류 • 뷰테인(부탄) • 브라운수소 • 브렌트유 • 블루수소 • 석유 • 석유화학 • 석탄 • 셰일가스 • 셰일오일 • 수소 • 수소연료 • 수소전기 • 순도 • 숯(목탄) • 압축가스 • 액체연료 • 액화가스 • 역청탄 • 연료 • 연료첨가제 • 연료화 • 연비 • 연소 • 연탄 • 오일샌드 • 오일셰일 • 옥탄가 • 용해가스 • 원유 • 유사경유 • 유연탄 • 유연휘발유 • 윤활유 • 일반휘발유 • 장작 • 점화 • 정유 • 정제 • 조개탄 • 주입 • 중유 • 중질유(中質油) • 중질유(重質油) • 증류 • 질소산화물 • 천연가스 • 천연자원 • 친환경연료 • 코크스 • 타르 • 텍사스유 • 프로페인(프로판) • 합성경유 • 핵연료 • 혼유 • 혼합가스 • 혼합기체 • 혼합연료 • 화석연료 • 화재 • 휘발유(가솔린)
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|
| 지역 : 지역, 지형, 기후, 날씨 □■⊕, 한국지리, 세계지리, 세계의 강, 세계의 바다, 세계의 섬, 국가, 도시, 아시아 도시, 유럽 도시, 북아메리카 도시, 세계의 도시, 신도시, 한국 행정구역, 북한 행정구역, 중국 행정구역, 일본 행정구역, 인도네시아 행정구역, 동남아시아 행정구역, 아시아 행정구역, 유럽 행정구역, 러시아 행정구역, 북아메리카 행정구역, 남아메리카 행정구역, 세계 행정구역, 한국 지역, 아시아 지역, 유럽 지역, 북아메리카 지역, 남아메리카 지역, 아프리카 지역, 세계 지역
|
|
|
| 날씨
|
가마솥더위 • 가을볕 • 강추위 • 고온 • 고온건조 • 고온다습 • 그늘 • 그림자 • 기온 • 기온차 • 꽃샘추위 • 날씨 • 냉기 • 냉파 • 늦더위 • 늦추위 • 다습 • 더위 • 등온선(등치선) • 등편차선 • 땡볕 • 뙤약볕 • 맑음 • 맹추위 • 무더위 • 볕 • 봄볕 • 불볕 • 불볕더위 • 불쾌지수 • 빛 • 삼복더위 • 삼한사온 • 상대습도 • 섭씨 • 습기 • 습도 • 습윤 • 실효온도 • 열기 • 열사병 • 열지수 • 온기 • 온도 • 온도계 • 온도차 • 온흐림 • 이상고온 • 이상난동 • 이상냉하 • 이상저온 • 일교차 • 일기 • 일기도 • 일사량 • 일사병 • 저온 • 절대습도 • 체감온도 • 추위 • 찜통더위 • 토출온도 • 폭염(혹서) • 폭염경보 • 폭염주의보 • 폭염특보 • 한기 • 한랭 • 한랭건조 • 한랭다습 • 한랭습윤 • 한파 • 한파경보 • 한파주의보 • 한파특보 • 햇볕 • 햇빛 • 햇살 • 혹한 • 혹한기 • 화씨 • 흐림
|
|
|
| 비
|
가랑비(잔비, 실비) • 가루비 • 가뭄 • 가을비 • 가을장마 • 강수 • 강수량 • 강우 • 강우량 • 개부심 • 갬 • 건들장마 • 건조 • 건조경보 • 건조주의보 • 겨울비 • 궂은비 • 꿀비 • 뇌우 • 는개 • 늦장마 • 단비 • 달구비 • 도둑비 • 떡비 • 마른장마 • 먼지잼 • 모다깃비 • 모종비 • 목비 • 무더기비 • 무지개 • 물방울 • 밤비 • 번개 • 벼락(낙뢰) • 보슬비 • 봄비 • 봄장마 • 부슬비 • 비 • 비꽃 • 빗물 • 빗방울 • 빗소리 • 빗줄기 • 산사태 • 산성비 • 소나기 • 수증기 • 술비 • 슈퍼셀 • 스콜 • 악뇌우 • 안개비 • 안개주의보 • 약비 • 억수 • 억수장마 • 여름비 • 여우비 • 웃비 • 응결 • 응결점 • 이슬 • 이슬비 • 이슬점 • 인공강우 • 일비 • 자드락비 • 작달비 • 잠비 • 장대비 • 장마 • 장마권 • 장마전선 • 장마철 • 장맛비 • 전선뇌우 • 증발 • 증발량 • 집중호우 • 찬비 • 채찍비 • 천둥 • 청천벽력 • 춘뢰 • 칠석물(칠석비) • 큰비 • 폭우 • 폭풍우 • 호우 • 호우경보 • 호우주의보 • 홍수 • 황사비
|
|
|
| 눈
|
가랑눈 • 가루눈 • 강설량 • 결로 • 고드름 • 길눈 • 날린눈 • 내부결로 • 눈 • 눈갈기 • 눈꽃 • 눈바람 • 눈발 • 눈보라 • 눈사람 • 눈사태 • 눈석임 • 눈석임물(눈석이) • 눈송이 • 눈싸움 • 눈폭풍 • 대설 • 대설경보 • 대설주의보 • 대설특보 • 도둑눈 • 떡눈 • 마른눈 • 발등눈 • 복눈 • 봄눈 • 빙정 • 서리 • 서릿발 • 성에 • 소나기눈 • 숫눈 • 신적설 • 싸라기눈(싸락눈) • 얼음 • 우박 • 인공눈 • 자국눈 • 잣눈 • 적설 • 적설량 • 진눈깨비 • 첫눈 • 최심신적설 • 최심적설 • 추상 • 포슬눈 • 폭설 • 표면결로 • 풋눈 • 함박눈
|
|
|
| 구름
|
고적운(양떼구름) • 고층운 • 구름 • 구름층 • 권운(새털구름) • 권적운 • 권층운 • 난운 • 난층운 • 뜬구름 • 먹구름 • 상층운 • 수직운 • 안개 • 적란운(비구름) • 적운(뭉게구름) • 중층운 • 층운(안개구름) • 층적운(두루마리구름) • 편적운 • 편층운 • 하층운 • 해무 • 흰구름
|
|
|
| 바람
|
가는바람 • 가을바람 • 간들바람 • 강풍 • 강풍경보(폭풍경보) • 강풍주의보(폭풍주의보) • 건들바람 • 겨울바람 • 계절풍 • 고기압 • 고요 • 고추바람 • 골바람(곡풍) • 공기 • 국지풍 • 극동풍 • 급변풍 • 기단 • 기류 • 기압 • 기압골 • 난기류 • 날파람 • 남동풍(동남풍) • 남서풍(서남풍) • 남실바람 • 남풍(마파람) • 냉풍 • 노대바람 • 높새바람 • 늦바람 • 대기 • 대기권 • 대기순환 • 대류권 • 더스트볼 • 돌풍(갑작바람) • 동풍(샛바람) • 된바람 • 등압선 • 디아블로 • 마에스트로 • 모래바람 • 모래폭풍 • 몬순(계절풍) • 무역풍 • 무풍 • 무풍지대 • 미풍 • 바람 • 보퍼트 풍력계급 • 봄바람 • 북동풍 • 북서풍(서북풍) • 북풍(된바람) • 블리자드 • 비바람 • 빌딩풍 • 사막풍 • 사이클론 • 산곡풍 • 산들바람 • 산바람(산풍) • 상승기류 • 서풍(하늬바람) • 성층권 • 센바람 • 소슬바람 • 수렴기류 • 수직기류 • 시베리아 고기압 • 실바람 • 싹쓸바람 • 약풍 • 여름바람 • 연풍 • 열권 • 열대저기압 • 옆바람 • 온난전선 • 온대저기압 • 온도풍 • 온풍 • 왕바람 • 왜바람 • 육풍 • 이동성 고기압 • 이동성 저기압 • 저기압 • 전선 • 제트기류 • 중간권 • 찬 공기 • 찬 바람 • 큰바람 • 큰센바람 • 탁월풍 • 태풍 • 태풍경보 • 태풍주의보 • 토네이도(용오름) • 파스칼(Pa) • 편동풍 • 편서풍 • 폭풍 • 푄현상 • 풍력 • 풍력계급 • 풍속 • 풍압 • 풍향 • 하강기류 • 하향격풍(미소격풍, 마이크로버스트) • 한랭전선 • 항공경보 • 해기차 • 해륙풍 • 해풍 • 허리케인 • 헥토파스칼(hPa) • 활강풍 • 황사 • 황사경보 • 황사주의보 • 황소바람 • 회오리바람 • 흔들바람(질풍)
|
|
|
| 해류
|
간만 • 간조 • 고파 • 난류 • 너울 • 라니냐 • 만조 • 물거품 • 물결 • 밀물 • 석수 • 쇄파 • 수괴 • 수온 • 심층수 • 썰물 • 엘니뇨 • 연안류 • 왕복조류 • 이안류 • 잔물결 • 장파 • 저층수 • 조류 • 조석 • 조차 • 중간파 • 중층수 • 지진 • 지진해일 • 지진해일경보 • 지진해일주의보 • 파도 • 폭풍해일 • 폭풍해일경보 • 폭풍해일주의보 • 표면파 • 표층수 • 풍랑(풍파) • 풍랑경보 • 풍랑주의보 • 한류 • 해류 • 해류도 • 해상경보 • 해수(바닷물) • 해양파 • 해양학 • 해일 • 해일주의보 • 해파 • 회전조류 • 흐름
|
|
|
| 기상
|
경보 • 기상 • 기상경보 • 기상관측 • 기상법 • 기상상황 • 기상예보 • 기상예비특보 • 기상이변 • 기상재해 • 기상주의보 • 기상특보 • 기상학 • 기상현상 • 예보 • 우주기상 • 일기예보 • 조드 • 주의보 • 특보
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|

 위키원
위키원