탄성

탄성(彈性, elasticity)은 어떤 물체가 외부에서 가해진 힘에 의해서 그 형태가 변형된 상태에서 힘이 제거되었을 때 물체의 원래 모양으로 되돌아가려는 성질을 뜻한다. 일상용어로는 탄력이라고도 부른다. 반대로 외부 힘이 제거되었는데도 원래 모양으로 되돌아가지 아니하고 변형된 상태에 머무르는 성질을 소성(plasticity)이라고 한다.

많은 물질은 탄성 범위 안에서는 형태를 바꾸어도 원래대로 돌아간다. 이 말은 보일이 처음 사용하였다. 탄성은 응력(stress)과 변형(strain) 사이의 선형 관계로 이루어지며 이를 선형 탄성이라고 한다. 고무 밴드와 잘 튀는 공을 예로 들 수 있다. 이 개념은 처음에 로버트 훅이 1675년에 언급하기 시작하였다. 이러한 선형 관계는 훅 법칙으로 불린다. 선형 탄성의 전형적인 모델은 "완벽하게 원래의 모습으로 돌아가는" 용수철이다.

상세

물체가 탄성을 가지는 이유는 물체마다 다르다. 예를 들어 금속의 경우 외부에서 힘이 가해지면 금속을 이루는 원자 살창(격자)(lattice)구조가 변형되며 에너지가 금속 내부에 쌓이게 된다. 이 때 외부 힘이 제거되면, 원자 살창구조는 원래 모습으로 돌아가며 쌓였던 에너지를 방출한다. 이 현상이 금속이 탄성을 가지는 이유이다. 한편, 고무 등 고분자 물질의 경우에는 탄성은 그 물질을 이루는 고분자 사슬이 힘을 받으면 늘어나거나 축소되었다가 힘이 제거되면 원래 길이로 돌아가면서 나타난다. 현실 세계에서 완벽하게 탄성만을 가지는 물체는 없으며, 대개 일정 정도의 외부 힘에 대해서 까지만 탄성 변형을 보인다.

탄성을 가지는 물체를 탄성체(elasic body) 라고 하며, 용수철이나 고무줄 등이 대표적인 예이다. 탄성체라도 작용하는 변형력이 어느 한계 이상 커지면 다시 평형상태로 복원되지 않게 되는데, 그 한계를 탄성한계(elastic limit) 또는 항복점(yielding point)이라고 한다. 공학에서는 재료의 탄성 특성을 대개 두 가지 매개변수로 나타낸다. 첫 번째는 영률(Young’s modulus)로, 가해지는 압력에 대해 변형이 얼마나 일어나는가의 비율로 정해지는 값이다. 영률 값이 클수록 그 재료는 변형시키기 어렵다. 두 번째 매개변수는 탄성한계로, 탄성변형의 한계를 벗어나 영구적인 변형이 일어나기 직전까지 재료 내부에 쌓인 변형력(stress)의 크기다. 탄성한계도 압력과 같은 단위를 갖는 물리 값이다. 예를 들자면 금속과 비교할 때 고무는 낮은 영률을 가져서 쉽게 변형되고, 높은 탄성한계를 가져 많이 변형된다. 변형력은 공학에서는 응력이라고 흔히 불리운다.

탄성체에 작용하는 변형력에 따라 변형되는 정도가 다른데, 변형력이 탄성한계보다 작은 경우 변형력과 변형되는 정도는 서로 비례관계가 있다는 것이 실험적으로 알려져 있다. 이를 훅의 법칙이라고 하며, 그 비례상수를 탄성률이라 한다. 영국 물리학자인 훅(Robert Hooke, 1635-1703)이 법칙을 발견하여 이름이 붙여졌다. 변형력이 탄성한계보다 작은 경우 탄성률이 클수록 같은 크기의 변형력에 대해 변형되는 정도가 더 작다. 금속 막대도 탄성체라고 할 수 있는데, 용수철이나 고무줄보다 탄성률이 커서 변형되는 정도가 덜 두드러진다. 탄성한계 안에서는 변형이 커질수록 외력이 해준 일도 더 커지므로 퍼텐셜에너지도 그만큼 더 커진다.

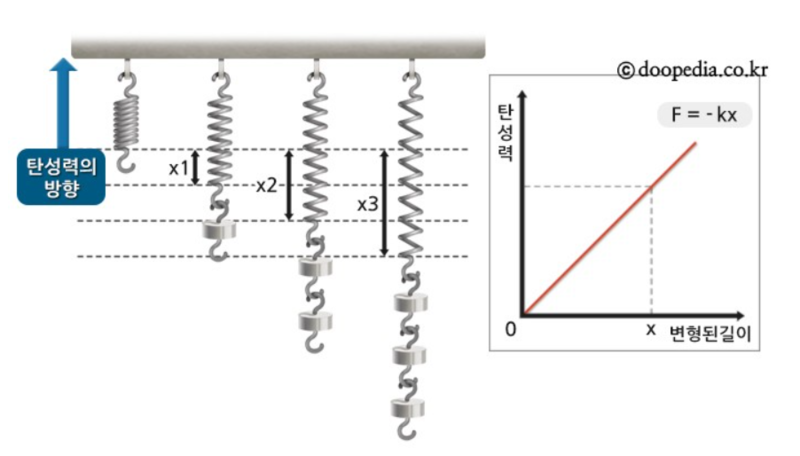
탄성한계 안에서 용수철이 평형상태보다 길이가 늘어나거나 줄어드는 경우 용수철을 평형상태로 되돌리려는 복원력이 작용하는데, 복원력은 용수철 한 쪽 끝에 물체가 연결되어 있는 경우 용수철이 이 물체에 작용하는 힘으로 나타낼 수 있다. 용수철의 복원력은 용수철이 평형상태로부터 늘어나거나 줄어든 길이에 비례하며, 이는 훅의 법칙의 한 형태라고 할 수 있다. 만일 용수철의 다른 쪽 끝은 고정되어 있고, 용수철에 연결된 물체의 위치 x를 평형상태에서 x=0 이라고 하면, 복원력은

F = -kx

로 표현된다. 여기서 k 는 양의 상수로 용수철 상수 또는 힘 상수라고 하며 탄성률에 비례한다. x > 0 이면 평형상태보다 길이가 늘어난 경우에 해당하고 x < 0 이면 평형상태보다 길이가 줄어든 경우에 해당한다.

체적탄성과 형상탄성

탄성은 크게 부피 변화에 대해 일어나는 체적탄성과 모양 변화에 대해 일어나는 형상탄성으로 나눌 수 있다. 고무공에 힘을 빼면 원상태로 되돌아가는 것은 기체의 체적탄성에 의한 것이다. 이에 대해 스프링의 탄력 등은 주로 형상탄성에 의해서 일어난다. 기체나 액체는 일정한 모양이 없으므로 형상탄성이 나타나지 않지만 고체의 경우, 형상탄성과 체적탄성이 함께 일어나며, 양쪽이 함께 나타나는 경우가 많다.

탄성에너지

힘을 받아 일시적으로 변형하는 물체는 밖으로부터의 힘을 잠재적 에너지로 저장하는 상태에 있다. 예를 들면 스프링은 압축됨으로써 에너지를 내부에 저장하며, 활은 시위를 당김으로써 에너지가 축적되므로, 갑자기 힘을 제거하면 이들 에너지가 한번에 밖을 향한다. 즉 변형하고 있는 탄성체는 위치에너지를 가지게 되는데 이것을 탄성에너지라고 한다.

참고로 탄성과 반대되는 개념으로 외부의 힘이 제거되었음에도 불구하고 물체가 원래 모양으로 돌아오지 않는 성질을 소성이라 한다.

의탄성

의탄성은 형상기억합금이 탄성을 발휘하여 미리 설정된 모습으로 돌아오게 하는 성질을 말하며 강철과 같은 일반 기계 부품에 쓰이는 용수철에 비해 보다 탄성 변형의 허용폭이 크다.

이를테면, 기계 부품으로서 형상기억합금으로 만든 용수철을 그 기계의 작동 온도보다 낮은 온도로 탄성을 회복하는 합금으로 용수철을 만들어 사용할 경우, 보다 큰 부하를 용수철에 걸 수 있기 때문에 공학쪽에서 보면 보다 유리하게 설계할 수 있다. 특히 탄성 회복 온도가 낮은 현상기억합금을 의탄성 합금이라고 말한다.

참고자료

• 〈탄성〉, 《위키백과》
• 〈탄성〉, 《물리학백과》
• 〈탄성〉, 《두산백과》

같이 보기

• 탄성변형
• 탄성에너지
• 탄성체
• 탄력
• 영률
• 변형력
• 소성

이 탄성 문서는 에너지에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

산업 : 산업, 산업혁명, 기술, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지 □■⊕, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지 에너지 SMR • 가속운동 • 가시광선 • 가열 • 각속도 • 감마선 • 감속운동 • 강력 • 고압 • 고온 • 고전역학 • 관성력 • 관성모멘트 • 광선 • 광속 • 광전자 • 광전효과 • 광합성 • 기압 • 냉각 • 냉방 • 뉴턴 • 대류 • 대체에너지 • 동력 • 동력원 • 라디오파 • 마이크로파 • 마찰 • 마찰계수 • 마찰력 • 마찰에너지 • 만유인력 • 만유인력의 법칙 • 무중력 • 물리에너지 • 바이오에너지 • 발열 • 발열반응 • 발화 • 방사선 • 방열 • 베타선 • 복사 • 복사선 • 복사에너지 • 부력 • 불 • 블루에너지 • 빛 • 빛에너지 • 삼투압 • 생물에너지 • 석유에너지 • 석탄에너지 • 섭씨 • 소리에너지 • 소수력 • 속력 • 수력 • 수력에너지 • 수소에너지 • 수압 • 수열 • 수열에너지 • 수직항력 • 신생에너지 • 신에너지 • 신재생 • 신재생에너지 • 알짜힘(합력) • 알파선 • 압력 • 압축응력 • 약력 • 양극선 • 양자역학 • 에너지 • 에너지밀도 • 에너지보존법칙 • 에너지원 • 에너지 효율 • 엑스선 • 엔트로피 • 역반응 • 역파장 • 역학적 에너지(기계에너지) • 열 • 열대류 • 열량 • 열복사 • 열분해 • 열에너지 • 열역학 • 열전도 • 열전도도 • 열전도율 • 열절연 • 열팽창 • 열팽창계수 • 열효율 • 온도 • 온도차 • 왕복에너지 • 왕복운동 • 운동에너지 • 원운동 • 원자력 • 원자력에너지 • 위치에너지 • 음극선 • 응력 • 인공태양 • 인장응력 • 인화 • 입자선 • 자외선 • 자유낙하 • 작용 • 재가열 • 재생에너지 • 저온 • 저압 • 적외선 • 전기에너지 • 전도 • 전자기력 • 절대온도 • 정반응 • 정지에너지 • 조력 • 조력에너지 • 조류에너지 • 줄 • 줄의 법칙 • 중력 • 중력에너지 • 지열 • 지열에너지 • 직사광선 • 직선운동 • 진동 • 진동에너지 • 진자 • 진자운동 • 천연에너지 • 청정에너지 • 친환경에너지 • 칼로리 • 탄성 • 탄성에너지 • 태양 • 태양광 • 태양광에너지 • 태양에너지 • 태양열 • 태양열에너지 • 텐서 • 파동 • 파력 • 파력에너지 • 파워 • 파장 • 폐기물에너지 • 폭발 • 풍력 • 풍력에너지 • 풍압 • 항력(드래그포스) • 해양에너지 • 핵반응 • 핵분열 • 핵분열에너지 • 핵붕괴 • 핵에너지 • 핵융합 • 핵융합에너지 • 화력 • 화씨 • 화학 • 화학에너지 • 회전 • 회전수 • 회전에너지 • 회전운동 • 흡열 • 흡열반응 • 힘 발전 교류발전기 • 마이크로 수력발전 • 물레방아 • 박테리아 발전소 • 발전 • 발전기 • 발전소 • 발전효율 • 변전소 • 비상발전기 • 소수력발전 • 소수력발전소 • 소형모듈원전(SMR) • 수력발전 • 수력발전소 • 원자력발전 • 원자력발전소 • 조력발전 • 조력발전소 • 조류발전 • 조류발전소 • 지열난방 • 지열발전 • 지열발전소 • 직류발전기 • 태양광발전 • 태양광발전소 • 태양광패널 • 태양열발전 • 태양열발전소 • 파력발전 • 파력발전소 • 풍력발전 • 풍력발전소 • 풍차 • 해양 온도차 발전 • 핵융합발전 • 핵융합발전소 • 화력발전 • 화력발전소 • 회전축 연료 CNG • LNG • LPG • 가스 • 가스충전소 • 가연성 • 갈탄 • 개질수소 • 경유(디젤) • 경질유 • 고급휘발유 • 고압가스 • 고체연료 • 그레이수소 • 그린수소 • 기체연료 • 나무 • 난방연료 • 두바이유 • 등유 • 땔감 • 면세유 • 무연탄 • 무연휘발유 • 바이오 • 바이오가스 • 바이오디젤 • 바이오매스 • 바이오에탄올 • 바이오연료 • 방사성물질 • 배기가스 • 배출가스 • 번개탄 • 부생수소 • 분별증류 • 뷰테인(부탄) • 브라운수소 • 브렌트유 • 블루수소 • 석유 • 석유화학 • 석탄 • 셰일가스 • 셰일오일 • 수소 • 수소연료 • 수소전기 • 순도 • 숯(목탄) • 압축가스 • 액체연료 • 액화가스 • 역청탄 • 연료 • 연료첨가제 • 연료화 • 연비 • 연소 • 연탄 • 오일샌드 • 오일셰일 • 옥탄가 • 용해가스 • 원유 • 유사경유 • 유연탄 • 유연휘발유 • 윤활유 • 일반휘발유 • 장작 • 점화 • 정유 • 정제 • 조개탄 • 주입 • 중유 • 중질유(中質油) • 중질유(重質油) • 증류 • 질소산화물 • 천연가스 • 천연자원 • 친환경연료 • 코크스 • 타르 • 텍사스유 • 프로페인(프로판) • 합성경유 • 핵연료 • 혼유 • 혼합가스 • 혼합기체 • 혼합연료 • 화석연료 • 화재 • 휘발유(가솔린) 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반

자동차 : 자동차 분류, 자동차 회사, 한국 자동차, 독일 자동차, 유럽 자동차, 미국 자동차, 중국 자동차, 일본 자동차, 전기자동차, 자동차 제조 □■⊕, 자동차 부품, 자동차 색상, 자동차 외장, 자동차 내장, 자동차 전장, 자동차 부품 회사, 배터리, 배터리 회사, 충전, 자동차 판매, 자동차 판매 회사, 자동차 관리, 자동차 역사, 자동차 인물 자동차 제조 기술 • 기술력 • 단종 • 마이너체인지 • 모델체인지 • 배지 엔지니어링(리뱃징) • 아이코닉 모델 • 연식변경 • 자동차 • 자동차 제조 • 제조 • 페이스리프트 • 풀체인지 • 플래그십 설계 CMF • VR모델 • 공기역학 • 기능 • 기능디자인 • 기능성 • 드로잉 • 디자이너 • 디자인 • 라인업 • 러기드 • 럭셔리 • 렌더링 • 리뷰 • 마닐라지 • 모델 • 모형 • 목업 • 미니멀리즘 • 비스포크 • 산업 디자이너 • 산업디자인 • 샘플 • 샤시디자인 • 설계 • 스케치 • 스타일 • 스타일리시 • 스포티 • 시각디자인 • 시제품 • 실내디자인 • 실루엣 • 실물 • 실외디자인 • 심미성 • 에어로 다이내믹 • 오퍼짓 유나이티드 • 인디오더 • 인사이드 아웃 • 자동차 디자인 • 자동차 디자이너 • 자동차 설계 • 제품디자인 • 제품 디자이너 • 클레이 • 클레이모형 • 테이프 • 테이프 드로잉 • 트라이아웃카 • 트렌디 • 패밀리룩 • 흐름도 프레스 가스절단 • 강 • 강도 • 강철 • 강판 • 고장력 • 고장력강 • 관재 • 구멍 • 굽힘 • 균열 • 금속 • 금속판 • 금형 • 금형기 • 납땜(납접) • 네킹 • 노칭 • 단조 • 드로잉 • 리스트라이킹 • 마킹 • 모양 • 모재 • 버링 • 벌징 • 벤딩 • 변형 • 보론강(붕소강) • 봉재 • 부재 • 블랭킹 • 비딩 • 사출 • 사출금형 • 사출금형기 • 사출기 • 성형 • 세퍼레이팅 • 셰이빙 • 소성 • 소성가공 • 소성변형 • 쇠 • 쇳물 • 스웨이징 • 슬로팅 • 슬리팅 • 시밍 • 아이어닝 • 아크절단 • 알루미늄 • 압연 • 압인 • 압접 • 압착 • 압축 • 압축가공 • 압축력 • 압출 • 업세팅 • 엠보싱 • 용가재 • 용접 • 용접봉 • 융접 • 익스팬딩 • 인발 • 인장력 • 장력 • 재드로잉 • 재료 • 전단 • 전단기 • 전단력 • 전단면 • 절단 • 정밀 블랭킹 • 제련 • 제련소 • 제진강판 • 제철 • 제철소 • 주름 • 철 • 철강 • 철강업 • 철판 • 초고장력 • 초고장력강 • 충격압출 • 컬링 • 컷오프 • 클래딩 • 탄성 • 탄성변형 • 트리밍 • 틀 • 판 • 판금 • 판재 • 패널 • 퍼포레이팅 • 펀치 • 펀칭 • 프레스 • 프레스가공 • 플래팅(스트레이트닝) • 플랜징 • 피어싱 • 합금 • 헤딩 • 형상 • 형재 • 형체 • 형태 • 형틀 도장 CMYK • RGB • 건조 • 고온도장 • 광선 • 광원 • 광택 • 광택제 • 구도막 • 구도막 제거 • 굽기 • 그림자 • 기포 • 농담 • 도금 • 도료 • 도료컵 • 도막 • 도막두께 • 도막두께 측정기 • 도색 • 도장 • 도장막 • 도장면 • 도장부위 • 도장장비 • 도포 • 독성 • 두께 • 롤러 • 마스킹 • 마스킹 테이프 • 명도 • 명암 • 무광 • 무광크롬 • 무늬 • 물감 • 미술 • 박리 • 반광 • 반사 • 반투명 • 발색 • 방청 • 배색 • 배합 • 백화현상 • 변색 • 보수도막 • 부식 • 분말 • 분무기 • 분사 • 분사장치 • 분진 • 분체도장(파우더코팅) • 불투명 • 불투명도 • 붓 • 붓펜 • 블렌딩 • 블렌딩 도장 • 빛 • 상도 • 상도도장 • 상수 • 상수도 • 색 • 색깔 • 색배합표(조색표) • 색상 • 색소 • 색조 • 색채 • 서페이서 • 소부 • 소부도장 • 스월마크 • 스크래치 • 스프레이 • 스프레이건 • 시너 • 실러 • 실러공정 • 아노다이징 • 안료 • 액체도장 • 액체소부도장 • 양감 • 언더코팅 • 에어브러시 • 열처리 • 염료 • 염색 • 오수 • 오폐수 • 오픈포어 • 용매(솔벤트) • 용액 • 용제 • 외관 • 요철 • 워터스팟 • 원색 • 유광 • 은폐력 • 음영 • 자연건조 • 재도장 • 저온도장 • 전색제 • 전착 • 전착도료 • 전착도장 • 전처리공정 • 점도 • 접착 • 접착력 • 조색 • 조색제 • 중도 • 중도도장 • 질감 • 착색 • 착색제 • 채도 • 채색 • 칠 • 침적 • 코팅 • 코팅막 • 크롬도금 • 클리어코트 • 탈색 • 투명 • 투명코팅막 • 트리거 • 틴팅(썬팅) • 팔레트 • 퍼티 • 페인트 • 페인팅 • 펜 • 폐수 • 표면 • 표면경화 • 표면처리 • 프라이머 • 피도물 • 피막 • 하도 • 하도도장 • 하수 • 하수도 • 하이그로시 • 화성처리 • 환풍기 • 희석 부품제작 3D 프린터 • 3D 프린팅 • 금속가공 • 기가캐스팅 • 기계가공 • 드릴링 • 리밍 • 메가캐스팅 • 모듈 • 모듈화 • 부품제작 • 소결 • 스폿페이싱 • 엔진조립 • 연마 • 옵션 • 절삭 • 절삭가공 • 절삭공구 • 주물(다이캐스팅) • 주조(캐스팅) • 주형 • 치수 • 카운터보어 • 카운터싱크 • 탭핑(탭가공) • 하이퍼캐스팅 의장조립 CKD • JIS • JIT • SKD • 골격 • 밀봉 • 반조립 • 배관 • 배선 • 부품조립 • 의장 • 의장라인 • 의장모듈 • 의장부품 • 의장조립 • 이동조립 • 장착 • 재조립 • 접합 • 조립 • 조립공장 • 조립라인 • 조립품 • 차체 • 차체조립 • 컨베이어 벨트 • 탑재 • 토요타 생산 시스템(TPS) • 패키징 • 포드시스템 • 프레임 • 회선 시험 강설시험 • 강우시험 • 계측 • 계측기 • 고온시험 • 더미 • 먼지터널시험 • 벨지언로 주행시험 • 사막주행시험 • 사이드 폴 테스트 • 성능 • 성능시험 • 수밀 • 시험 • 실험 • 오류 • 오작동 • 오차 • 작동 • 재시험 • 재실험 • 저마찰로 주행시험 • 저온시험 • 주행시험 • 진동시험 • 충돌시험 • 측정 • 측정기 • 타이어시험 • 테스트 • 평가 • 풍동시험 • 휠 밸런스 • 휠 얼라인먼트 검수 PDI • PDI센터 • 검사 • 검수 • 검증 • 검토 • 규격 • 기능검사 • 납기 • 납품 • 리콜 • 반품 • 발견 • 불량 • 불합격 • 비정상 • 사양 • 상세사양 • 수밀검사 • 수정 • 양호 • 완성 • 이상 • 자동차 안전도 평가 • 재검사 • 점검 • 정상 • 타각 • 품질 • 품질관리 • 품질보장 • 품질보증 • 하자 • 합격 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반