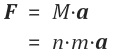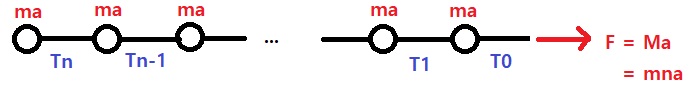장력
장력(Tension, 張力, 문화어: 켕김힘)은 물리학에서 끈, 체인, 막대 등 1차원적 1차원 연속체의 한 점에 걸리는 힘이다. 다른 말로 질량을 길이의 함수로 보았을 때 길이에 대해 미분한 양이 된다. 질량이 없는 경우 장력은 모든 끈에 균일하다. 장력은 언제나 끈의 방향과 나란하다. 물리학에서 장력은 힘이 아니지만 힘의 단위를 가지며 뉴턴(N)으로 측정된다. 보통의 일반 역학에서 대부분 장력을 계산할 때 끈의 무게는 무시할 만큼 작다고 가정한다. [1]
목차
[숨기기]개요[편집]
장력은 줄이나 물체의 끝부분에서 그 줄이나 막대에 연결되어 있는 물체에 대해 연결부에서 줄의 방향으로 힘을 가한다. 줄에 연결된 물체의 계에서는 두 가지의 기초적 가능성이 존재한다. 가속도가 0이여서 계가 평형상태에 있거나 가속도가 있지만 계의 알짜힘은 일정한 경우이다. 원자수준에서 원자나 분자는 전자기적 인력을 갖는데 원자나 전자를 잡아당겨 멀어지게 하면 전자기 퍼텐셜 에너지를 갖게 되며 이는 곧 장력을 만들어낸다. 장력은 줄이나 막대의 늘어난 길이를 복구시키기 위해 서로 붙어있는 물체를 잡아당기게 한다. 줄이 당겨질 때 줄을 구성하는 입자간의 당기는 힘으로 인해서 퍼텐셜 에너지가 증가한다. 장력의 존재 덕분에 현악기가 탄생할 수 있었다. 피아노와 하프시코드를 비롯한 타현악기와 모든 현악기는 장력과 탄성력의 존재로 소리를 낼 수 있다. 자전거의 체인, 혹은 전차와 중장비에 들어가는 무한궤도같이 불연속적인 조각 마디들로 이루어진 물체들에도 장력이 작용한다. 체인이나 궤도가 이탈하는 사고를 막기 위해서는 팽팽함에 영향을 주는 장력을 조절하는 게 중요하다. 줄이 팽팽하지 않아도 장력은 존재한다. 줄을 잡아 당길 때 양쪽 끝이 완전히 팽팽해지지 않더라도, 자신이 잡아당기고 있는 부위를 다른 부위가 따라오기 때문에 이것은 장력의 증거이다. 장력이 없으면 따라 오지 않을 것이다. 10N의 물체를 실에 걸었을 경우 실에 작용하는 장력 또한 10N이며 실을 20N으로 잡아당겼을 경우 실에 작용하는 장력은 역시 20N이 된다.[2][3]
1차원 연속체에서의 장력[편집]
장력은 음의값이 아닌 스칼라양이다. 장력이 없다면 늘어진 상태인 것이다. 실이나 줄을 질량이 없지만 길이는 있는 1차원 물체라고 이상화해보자. 만약 실이 굽지 않을경우 장력은 실의 모든부분에서 일정하며, 실의 양 끝에서 작용하는 힘의 크기는 동일하다. 뉴턴 제3법칙에 따라 이 힘들은 실과 붙어있는 물체에서 실에 가해지는 힘의 크기와 같다. 만약 실이 도르레에 걸려있을 경우, 도르레가 질량과 마찰력이 없는 이상적 상황이라면, 실에 작용하는 장력의 크기는 동일할 것이다. 끈이 진동할 때 진동수는 끈의 장력에 의존한다. 진동수는 뉴턴법칙을 통해 이끌어 낼 수 있다. 줄의 미세한 부분들은 각각 이웃한 부분들과 서로 잡아당기며 힘의 크기는 줄의 위치에 관계없이 동일하다. 위치 x에 따른 장력의 크기는 t(x)}이다.
만약 실이 굽어있을 경우 두 이웃한 부분에서 서로 잡아당기는 힘의 크기는 합해서 0이 되지 않을것이다. 따라서 실의 부분에는 알짜힘이 가해지며 가속도가 생기게 된다. 이 알짜힘은 복원력이며, 스튀름-리우빌 이론에 따르면 실의 움직임은 횡파이며, 다음의 방정식으로 해를 구할 수 있다.
줄이라는 것은 원자나 분자 수준에서 봤을 때 연속체의 집합이다. 꼬여있는게 없이 그냥 등간격으로 연결되어 있다고 가정을 한다.
한쪽에서 당길 때[편집]
그런데 이 줄을 제가 오른쪽에서 F라는 힘으로 잡아당겼다고 하고 분자간에 서로 당기는 힘이 존재하지 않는다면 아래와 같은 상황이 벌어진다.
하지만 실제로는 분자 사이에 당기는 복원력이 존재하고 있기 때문에 분자의 상대적 위치가 보존되어야 한다. 줄의 전체 질량을 M라고 하고 하면 F=Ma 가 성립된다. 그런데 각 분자가 장력에 의해서 서로 끌어당겨서 상대적인 위치를 보존한다고 하면 결과적으로 모든 분자는 동일한 가속도로 운동하고 있어야 한다. 분자의 개수를 n이라고 하면 다음과 같은 식이 성립한다.
생각을 좀 단순하게 하기 위해서 분자들 간에 가상의 줄이 연결되어 있다고 하면 그 가상의 줄은 질량이 없다. 그냥 거기에 힘이 작용한다는 것을 설명하기 위해서 넣은 가상의 줄이므로 분자 사이의 공간에 적용되는 힘이라고 보셔도 된다.
T0에서는 전체 분자를 끌고 와야 한다. 전체 분자에 적용되므로 T0=mna =Ma =F이다.
T1에서는 n-1개의 분자를 끌고 와야 한다. 그러므로 T1= m(n-1)a이다. 이런 식으로 했을 때 마지막 Tn 에서는 1개의 분자를 끌고 와야 하므로 Tn=ma이다.
양쪽에서 당길 때[편집]
이제는 양쪽에서 이 분자로 구성된 줄을 끌고 있는데 양쪽 다 F라는 힘으로 끌고 있다고 하면
여기에서 힘의 합력은 0이다. F가 반대 방향으로 작용한다. 그러면 가속도 a=0이다. 장력은 음의 값이 아닌 스칼라양이다. 장력에는 방향이 없다. 물리학에서 장력은 힘이 아니지만 힘의 단위를 가지며 뉴턴으로 측정된다. 그러므로 작용하는 힘에 대한 반작용으로서의 장력들이 모두 합쳐야 한다.
결국 각 분자 사이에서는 동일한 장력이 발생한다. 이를 "평형상태의 계"라고 설명하고 있다.
천장에 매달린 공[편집]
천장에 고정된 끈에 매달린 공이 있을 때 거기에 작용하는 힘들을 도식화하고 있는데 각 지점에서의 장력에 대해 복합적으로 고민해 볼 수 있는 단초가 된다.
줄이 천장에 매달려 있을 때 천장과 붙은 부분에서는 수직항력에 대한 장력이 발생하고 공에 붙은 부분에서는 중력에 대한 장력이 발생한다. 줄 중간에서는 수직항력과 중력에 대한 장력이 발생한다.[4]
3차원 연속체에서의 장력[편집]
3차원에서는 면적이 생긴다. 일반적으로는 단면적에 대한 축방향력을 장력으로 사용한다. 막대나 트러스같은 3차원 연속체의 끝부분에서 가해지는 힘을 표현할 때도 장력을 이용한다. 막대를 늘리거나 할 때 이를 이용한다. 힘 또는 단위 단면적당 힘에 대해 늘어난 정도를 계산할 경우 잘 안될 것이므로 공학을 목적으로는 장력보다는 변형력 = 축방향력/단면적으로 계산하는 것이 더 나을 것이다. 변형력은 텐서의 3x3행렬이며 변형력 텐서의 성분 σ ₁ ₁ 은 단위 면적당 인장력이다(또는 단위 면적당 압축력인데, 막대가 늘어나는 경우가 아닌 압축되는 경우에는 이 성분을 이용해서 음수를 나타낸다).
평형상태의 계[편집]
모든 힘의 합이 0 일 때 계는 평형상태에 있다.
예를 들어, 계 내에 수직한 방향으로 등속으로 낙하하는 물체에 장력 T의 실이 걸려있다고 생각해 보자. 계는 일정한 속도를 가지며, 물체를 위로 잡아당기는 장력의 크기와 아래로 잡아당기는 중력의 크기가 같으므로 평형상태에 있다고 할 수 있다.
알짜힘이 존재하는 계[편집]
가해진 힘이 균형을 이루지 못해 계 내에 알짜힘이 존재할 경우 힘의 합력은 0이 아니다. 알짜힘과 가속도는 함께 존재한다.
예를 들어 위의 상황과 같지만 물체가 양(+)의 가속도를 가지며 아래 방향으로 속도가 점점 증가한다고 가정해 보자. 이 상황에서 물체에는 알짜힘이 가해지며 다음과 같다.
최대 인장 강도[편집]
장력은 주어진 힘에 대한 반작용으로 발생한다. 주어진 힘에 의해서 원자나 분자가 당겨질 때 위치를 복원하려고 발생하는 반작용 힘이다. 그래서 힘이 세질수록 장력도 세다. 어느 한계에 도달하면 복원하려는 힘(장력)보다 당기는 힘이 더 세지게 된다. 이렇게 되면 원자나 분자의 결합이 떨어지게 된다. 절벽에서 어떤 사람이 내 손을 잡고 매달려 있는데 처음에는 손바닥을 잡다가 점점 미끄러져 손끝으로만 버티다가 완전히 손에 떨어지는 것을 생각해 볼 수 있다. 장력으로 버틸 수 있는 최대 힘을 최대 인장 강도라 부른다. 이것도 3 차원이라서 단면적을 기준으로 한다. 인장 강도(tensile strength, TS) 또는 극한 강도(ultimate strength)라고 하는 극한 인장 강도(Ultimate tensile strength, UTS)는 재료의 세기를 나타내는 힘으로 재료가 절단되도록 끌어당겼을 때 견뎌내는 최대 하중을 재료의 단면적으로 나눈 값을 말한다. 인장 강도는 장력 강도라고 하기도 한다.
현대 물리학에서 실[편집]
특수 상대성 이론에서 실같이 생긴 물체(쿼크 사이의 상호작용에 쓰이는 실 모델이나 끈 이론의 끝 같은)들은 장력을 가진다. 이 끈(실)들은 끈들의 세계면에 의해 분석되고 에너지는 보통 끈의 길이에 비례한다. 장력은 끈의 늘어난 정도에 무관하다. 늘릴 수 있는 끈에 대해서는 훅 법칙이 적용된다.
각주[편집]
- 이동 ↑ 〈장력〉, 《위키백과》
- 이동 ↑ 〈장력〉, 《나무위키》
- 이동 ↑ 〈장력(tension)〉, 《사이언스올》
- 이동 ↑ lifeisforu, 〈장력(Tension)〉, 《티스토리》, 2019-06-26
참고자료[편집]
- 〈장력〉, 《위키백과》
- 〈장력〉, 《나무위키》
- 〈장력(tension)〉, 《사이언스올》
- lifeisforu, 〈장력(Tension)〉, 《티스토리》, 2019-06-26
같이 보기[편집]

 위키원
위키원