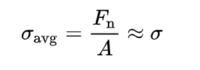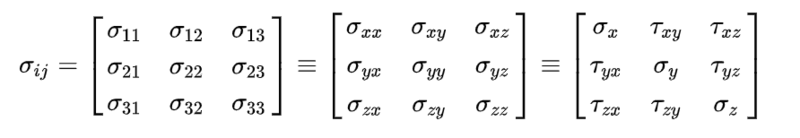응력
응력(stress)은 외력(外力)이 재료에 작용할 때 그 내부에 생기는 저항력을 말한다. 변형력이라고도 하고 내력(內力)이라고도 한다.
응력은 외력이 증가함에 따라 증가하지만 이에는 한도가 있어서 응력이 그 재료 고유의 한도에 도달하면 외력에 저항할 수 없게 되어 그 재료는 마침내 파괴된다. 응력의 한도가 큰 재료일수록 강한 재료라고 할 수 있으며, 또 외력에 의해 생기는 응력이 그 재료의 한도 응력보다 작을수록 안전하다고 할 수 있다. 그러나 응력의 크기로 재료의 강한 정도를 나타내면 같은 재료라도 단면적이 큰 것일수록 응력의 한도가 커지므로 강한 정도가 다르게 나타나고 또 다른 재료와의 세기를 비교하는 데도 불합리해진다.
따라서 단위면적에 생기는 응력의 크기를 구하면 재료의 단면적이 달라도 일정한 값이 되어 재료의 강도를 알아보는 데 편리하다. 이와 같이 응력을 단위면적에 대한 크기로 나타낼 때 이것을 단위응력 또는 응력도(應力度)라고 한다.
일반적으로 응력이라고 하면 단위응력을 말한다. 이에 대해 단면 전체에 생기는 응력의 합을 전응력(全應力)이라고 하며 단면 전체에 작용하는 전응력은 외력과 같으므로 단위면적에 대한 응력은 다음과 같이 나타낸다.
응력 =외력/단면적 응력의 단위는 힘 및 넓이의 단위에 따라 kgf/Cm², kgf/mm² 등이 사용된다.
정의[편집]
응력은 역학에서 단위면적당 작용하는 힘을 뜻한다. 오귀스탱 루이 코시가 1822년 처음 고안했다.
사실상 응력의 개념은 연속체(Continuum)라는 가정 아래 성립할 수 있다. 물체 내부의 경우, 가상의 단위부피를 설정해서 그 가상의 표면 바깥에 작용하는 힘을 계산하기 때문이다. 여기서 '가상의 힘'은 크게 두 종류가 있는데, 표면힘(Surface Force)과 몸체힘(Body Force)이다. 표면힘은 표면에 평행한 힘이며, 몸체힘은 표면에 대하여 수직 방향인 힘이다.
응력의 SI단위는 파스칼(Pa)이다. 압력과 같은 단위지만, 압력과 응력은 전혀 다른 개념이다.
일반적인 단면봉(Prismatic Bar)의 경우, 수직응력(Normal Stress)은 바깥쪽(Tension) 또는 안쪽(Compression)으로 작용한다. 변형률(Strain)과의 연관성 때문에, 보통 바깥쪽 응력을 양으로, 안쪽 응력을 음으로 본다. 이 경우, 보통은 계산의 편리성을 위해 모든 단면적에 고르게 힘이 작용한다라고 가정하고 평균값을 사용하는 경우가 많다. 즉,
실제로는 모든 지점마다 작용하는 응력의 값이 다르다. 때문에 코시는 이를 표현하기 위해 텐서를 사용했다.
이 방식은 축이 변할 경우 값이 어떻게 바뀌는지 계산하는 것이 힘들다는 단점을 가지고 있다. 이를 보완하기 위해 Mohr's Circle을 사용한다. 또한 코시 텐서는 작은 변형에 맞는 방식이기 때문에, 큰 변형의 경우 다른 방식을 사용한다.
응력의 종류[편집]
응력에는 수직응력 · 전단응력(剪斷應力) · 휨응력 등이 있다.
①수직응력 : 인장응력 · 압축응력 등이 있으며 재료의 축(軸) 방향으로 외력 P(=N)가 작용할 때의 응력은 임의 단면의 전면에 분포되어 생기며 이 단면의 단위면적에 대한 인장력을 인장응력이라고 한다. 또한 외력 P의 작용이 압축일 때는 임의 단면의 단위면적에 대한 압축력을 압축응력이라고 한다. 이와 같이 단면에 수직으로 생기는 응력을 통틀어 수직응력이라고 한다.
재료의 단면적이 A일 때, 수직응력은 =N/A=P/A가 된다.
부호는 인장응력을 +, 압축응력을 -로 표시한다.
② 전단응력 : 전단력에 의해 생기는 응력. 외력 P가 극히 작은 미소거리 x 사이에 작용하여 파선과 같은 모양의 변형이 생겨 비기고 있을 때는 재료의 축방향에 직각인 임의의 단면에는 전단응력 가생기므로 그 합력은 전단력 S의 크기와 같아서 S=P가 된다.
따라서 전단응력 의 분포가 균등하면 전단응력은 =S/A=P/A가 된다.
③ 휨응력 : 휨 모멘트(bend-ing moment)가 일어나는 재료에서는 재료의 축 방향과 수직 단면의 어떤 범위에 압축응력이 생기고 동시에 나머지 부분에는 인장응력이 생겨 단면의 상하 끝부분에서 최대 응력이 생기지만 그 경계가 되는 부분에는 응력이 생기지 않는다.
이와 같이 휨 모멘트로 인해 생기는 수직응력을 휨응력이라고 한다. 부호는 휨 모멘트로 인해 단면의 각 부분에 생기는 수직응력의 종류에 따라 +, -를 정한다.
휨응력이 0이 되는 경계선을 중립축이라 하고 중립축과 재료의 축을 포함하는 면을 중립면이라고 한다. 휨응력은 중립축에서 가장 먼 위치에서 +, -로 각기 최대가 된다. 이것을 연응력(緣應力)이라고 한다.
휨 모멘트를 M, 단면계수(단면 모양과 치수에 따라 결정되는 특정값)를 M라 하면 연응력은 b=M/Z이 된다.
응력-변형율 선도[편집]
탄성 한계 내에서의 응력과 변형율의 관계는 위에 설명해놓았지만, 탄성 한계를 넘어간 영역에서의 응력과 변형율의 관계는 실험을 통해 알아내는 수밖에 없다.
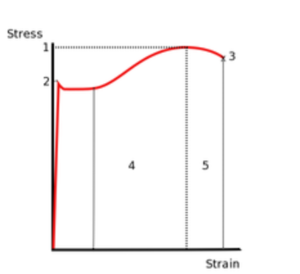
오른쪽 선도는 재료 중에서 연성 재료의 응력-변형율 선도이다. (Stress-Strain Curve/Diagram)
오른쪽 선도에서 원점부터 2까지 응력과 변형율이 비례관계를 가지는 구간을 탄성 구간(Elastic Region)이라고 한다. 이 구간 안에서는 탄성이 지배적으로 작용한다. 때문에 변형율이 탄성 구간 안에 있으면 재료는 탄성에 의해 원래 모습으로 돌아오게 된다.
위 선도에서 탄성 구간을 제외한 나머지 구간은 소성 구간 (Plastic Region)이라고 한다. 이 구간 안에서는 소성이 지배적으로 작용한다. 때문에 응력이 소성 구간까지 올라가면 재료는 다시 원래 모습으로 돌아올 수 없다.
그러나, 소성 구간에서 탄성이 작용하지 않는 것은 아니다. 재료의 변형율이 소성 구간의 중간 어느 지점까지 커지도록 한 후 재료에 힘을 가하는 것을 멈추면 재료는 그 변형된 그대로 가만히 있는 것이 아니라, 탄성에 의해 모습을 어느 정도 복원한다. 이를 탄성 복원(Elastic recovery/Spring back)이라고 한다.
만약 재료가 소성 구간에 있는 그래프 위의 임의의 점 P의 변형율까지 변형되었다가 응력이 사라질 경우, 재료는 점 P를 지나고 탄성 구간에서의 기울기와 똑같은 기울기를 가지는 직선이 가로축과 만나는 지점의 변형율로 되돌아간다. 그렇게 해서 점 P의 변형율보다는 적지만 값이 0은 아닌 변형율로 재료의 모양이 고정된다. 이때 새롭게 고정된 재료의 변형율을 영구 변형(permanent deformation/permanent set)이라고 한다.
위 선도를 보면 2에서 거의 수평으로 진행하는 구간이 있는데, 이 구간이 시작될 때의 응력을 항복 응력(Yield Stress) 혹은 항복 강도(Yield Strength)라고 하고 항복 구간이 시작되는 지점을 항복점이라고 한다. 이 응력에서는 응력이 변하지 않거나 조금만 변해도 변형율이 마구마구 늘어난다. 조금 두꺼운 쇠막대를 구부리다보면 어느 순간 확 굽어지는 경우가 있는데, 이때 바로 쇠막대에 가한 힘이 발생시긴 응력이 항복 응력을 넘어가서 그렇게 되는 것이다.
이 항복 응력 이후에 재료가 본격적으로 소성 구간으로 진입하고, 변형이 심해져 하중을 부담하는 능력이 떨어지거나 기계에서 이탈하는 경우가 생기기 때문에 보통 이 항복 응력보다 작은 적당한 응력을 허용 응력(Allowable Stress)으로 설정하곤 한다.
이는 실제 현장에서는 매우 중요하다. 실제 구조물이나 기계에서 부재에 작용하는 응력이 허용응력을 넘어설 경우 매우 위험할 수 있으며, 재료가 버틸 수 있는 최대한의 응력을 기준 강도라고 하고 연성 재료의 경우 항복점에서의 응력이 기준 강도이다. 이때 기준 강도를 허용 응력으로 나눈 것이 안전율(Safety Factor)이다. 당연히 안전율이 높을수록 좋다.
즉, 허용 응력 = 항복 응력 / 안전도. (A.Stress = Y.Stress / SF)
위 선도의 소성구간에서 가장 큰 응력이 나타나는 점을 극한 응력(Ultimate Tensile Stress) 혹은 극한 강도(Ultimate Tensile Strength)라고 한다.
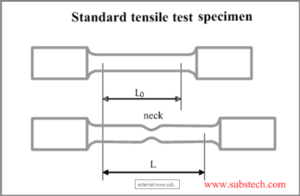
실험 도중에, 재료에는 극한 응력이 나타나기 조금 전부터 넥킹(Necking)이 일어난다. 가래떡의 예를 들어보면, 가래떡을 서서히 잡아당기면 가래떡 전체가 길게 늘어나다가 어느 순간 중간 부분이 다른 부분에 비해 잘록해진다. 이것이 바로 넥킹이다. 비록 실제 넥킹은 극한 강도가 나타나기 이전부터 나타나지만, 편의를 위해 극한 강도 이후의 구간을 '네킹 구간'이라고 부른다.
극한 응력 이후에는 응력의 크기가 작아지는데, 이는 실험의 한계로 인해 나타나는 것이다. 사실 넥킹이 일어나는 부위에서 응력-변형율의 관계는 일정하진 않아도 양(+)의 기울기를 가지는 관계이다. 하지만 이는 세로축의 물리량이 응력이기 때문에 나타나는 일이다. 넥킹이 일어나는 부위는 계속해서 잘록해지므로 힘이 그대로여도 넥킹에 의해 '힘/면적'인 응력의 크기는 계속 커진다. 하지만 우리가 실험을 통해서 응력을 측정할 때 대입하는 면적은 여전히 넥킹이 일어나지 않은 재료의 원래 단면적이다. 때문에 극한 강도 이후에 힘이 작어져도 변형이 계속되는 것이 마치 응력이 작아져도 변형이 계속되는 것으로 보이는 것이다. 실제로는 힘이 작아져도 면적이 작아지는 속도가 더 빨리 실제 응력은 계속 커지고 있다.
그래프가 어느 변형율에 이르면 끊어진다. 재료 자체가 파괴(fail)된 것이다. 그때의 응력을 가리켜 파괴응력(Rupture stress)라 한다.
재료의 종류에 따른 응력-변형율 선도[편집]
우리가 쓰는 고체 재료들은 대부분 연성 재료와 취성 재료로 나눌 수 있다.
연성 재료는 철근처럼 인장과 압축이 자유로우며 항복강도가 존재하는 재료들을 말한다. 연성 재료의 응력-변형율 선도는 위에서 설명한 그래프와 거의 일치한다. 이러한 연성 재료는 기준 강도가 항복 응력이기 때문에, 설계 할 때 항복 응력을 허용 응력(설계자가 지정, 실제로 현장에서 가해는 응력보다 조금 크게 설정된다.)으로 나눈 값을 '안전율'이라고 하고, 안전율이 높을수록 의외의 상황에 따른 과부하를 잘 견딜 수 있다.
취성 재료는 유리, 콘크리트, 세라믹, 지구의 지표면처럼 항복강도가 존재하지 않는 재료들을 말한다. 이러한 재료들은 탄성 구간을 넘어 소성구간에 접어들면 거의 즉시 파괴된다. 취성 재료의 응력-변형율 선도는 탄성구간밖에 존재하지 않으며, 항복 응력이 거의 극한 강도와 동일하다. 따라서 기준 강도 또한 극한 강도이다. 변형이 일어나면 변형이 한 지점에서 집중적으로 일어나다가 변형이 집중적으로 일어난 부분이 파괴되며 그 부분을 중심으로 균열이 생기는 연성 재료와는 달리, 변형이 재료 전체에서 일어나다가 파괴가 되는 순간 축적되어 있던 탄성 에너지가 재료 전체로 퍼지며 균열이 빠르게 확산되는 것이 특징이다. 이런 균열이 시작되는 지점은 표면에 흠(flaw)이 가거나 내부에 공동(void)이 생기는 등의 이유로 응력이 집중/증폭(stress concentration)되는 지점으로, 재료 전체에서 구조적으로 가장 취약한 부분에서부터 파괴가 시작된다. 이는 사슬을 팽팽하게 당길 때 가장 약한 고리가 가장 먼저 끊어지는 것(weakest link)으로 비유할 수 있다.
동영상[편집]
참고자료[편집]
같이 보기[편집]

 위키원
위키원