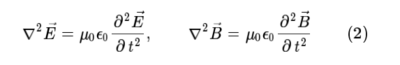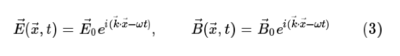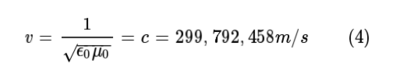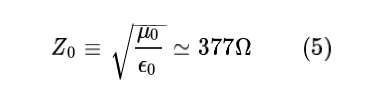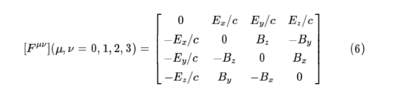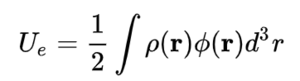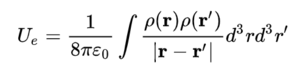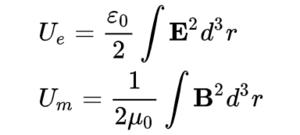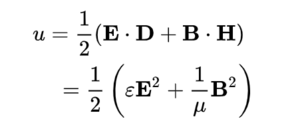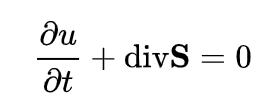전자기장
전자기장(電磁氣場, electromagnetic field, 약자 EMF)은 벡터장인 전기장과 자기장을 총칭하여 이르는 말이다. 전기장의 힘, 전속밀도와 자기장의 힘, 자속밀도가 시간의 흐름에 따라 변화하는 경우에는 서로 상호작용에 의해서 한층 더 변화해 가므로 이 둘을 아울러 전자기장으로 정리해 부르며, 특수 상대성 이론에서는 전자기장 텐서라는 하나의 객체로서 나타내어진다.
전자기장의 변동이 파동으로서 공간을 통해 전파되는 현상을 전자파라고 한다. 전자기장의 시간 변화는 맥스웰 방정식 및 양자전기역학을 통해 계산할 수 있다.
개요[편집]
전기장 · 전기력선속(電束)밀도 · 자기장 · 자기력선속밀도를 통틀어 일컫는다.
전기력선속밀도와 자기력선속밀도가 시간적으로 변화하는 경우에는 전기장과 자기장은 서로를 유기(誘起)하며 또한 서로 옮기고 바뀌므로, 전기장과 자기장을 별개의 것으로 생각할 수 없다. 이와 같은 경우에 특히 전자기장이라고 말하는 경우가 많다. 시간적으로 변화하지 않는 경우에는 전기장과 자기장은 각각 정전기장(靜電氣場)과 정자기장(靜磁氣場)으로도 불리며, 따로따로 생각할 수 있다. 전자기장이 파동으로서 공간을 전파할 경우, 이것을 전자기파라 한다.
전자기장은 벡터장으로서, 보통 전기장을 E, 전기력선속밀도를 D, 자기장을 H, 자기력선속밀도를 B로 나타낸다. 이것들은 공간좌표와 시간의 함수이다. 전기장은 에너지 · 운동량 · 각운동량(角運動量)을 갖는 물리적 실체이며, 물질과 상호작용한다. 이것을 전자기 상호작용이라 한다. 전자기 상호작용은 상대성이론에 의하면 근접 작용으로 해석되어야 하며, 자연계의 기본적인 4가지 상호작용(다른 3가지는 중력 상호작용, 강한 상호 작용, 약한 상호작용) 중 하나이다.
전자기장의 개념을 처음으로 명확히 파악한 사람은 M. 패러데이이며, 이를 수식화(數式化)한 사람은 J. C. 맥스웰인데, 전자기장의 여러 성질은 맥스웰의 전자기 방정식에 따른다. 전자기장의 개념의 영향으로 중력상호작용 (만유인력)에도 중력장(重力場)의 개념이 도입되었다. 당시 보급된 장(場)의 개념은 장을 물질 사이에 서로 미치는 힘(물질간의 상호작용)의 담당자로 본것이다. 이로써 고전물리학에서의 자연관으로서, 물질과 장의 이원론(二元論)이 형성되었다. 당초 전자기장을 기계론적 모형으로 해석하려는 시도에서 에테르 개념이 도입되었는데, 실체로서의 에테르는 실험적으로 부정되었다. 1905년 아인슈타인의 특수상대성이론의 출현은 고전물리학에서의 장의 개념에 변화를 가져왔다. 전자기장의 존재와 운동은 공간(또는 진공) 그 자체의 속성의 일부로서 해석하게 되었으며, 공간에 물리적 성질이 부여되었다. 그 후 양자역학의 성립에 의해 물질이나 장이 보여 주는 이중성, 즉 입자성과 파동성은 합리적으로 정식화되어, 이원론적 대립이 해소되었다. 이로써 장의 양자론에 입각, 양자화 된 전자기장을 광자(光子)로 해석하는 장의 일원론이 성립되었다.
빛의 전자기장[편집]
빛은 전기장과 자기장이 서로를 유도하며 퍼져 나가는 전자기파이다. 오른쪽 그림은 서로 수직인 방향으로 진동하는 전기장 E와 자기장 B의 모습을 보여준다. 이처럼 전자기파에는 전기장과 자기장이 공존하므로, 빛이 있는 공간은 전자기장이다. 전자기를 지배하는 맥스웰 방정식으로부터, 전류나 전하가 없는 공간에서의 전자기장에 관한 식을 얻을 수 있다.
여기서 μ₀, ε₀ 는 각각 진공의 투자율과 유전율이다. 식 1의식들을 연립하면 식 2와 같은 미분방정식을 얻을 수 있다.
식 2의 두 미분방정식은 같은 꼴이며, 그 해는 주어진 공간 (χ)과 시간 t에 대하여 사인파 또는 복소수의 파동 형태로 다음과 같이 주어진다.
여기서 k는 파수(wavenumber)로서 파동의 진행방향을, w는 각진동수로서 위상 변화의 빠르기를 나타낸다. 파동 전파의 위상속도(phase velocity) v=w/k는 식 4처럼 결정된다.
즉, 전류와 전하가 없는 공간에서의 전자기장은, 빛의 속도 c로 진행하는 전자기파 형태로만 존재할 수 있다는 것을 알 수 있다. 또한 전자기파의 임피던스는 전기장 E의 진폭과 자기장 H의 진폭의 비로 정의되는데, 진공에서의 임피던스는 아래 식 5로 결정된다.
특수상대론과 전자기장[편집]
아인슈타인의 특수상대성 이론에 의하여, 전기장과 자기장이 별개의 물리량이 아니라 관측자의 속도에 서로 변환되어 보일 수 있는 관계라는 것이 알려져 있다. 시간과 공간(t, x, y,z)의 4차원 표현에서 전기장 (Ex, Ey, Ez)와 자기장 (Bx, By, Bz)를 포함한 전자기장 텐서(electromagnetic field tensor)Fμν(소문자 위첨자)는 다음의 4×4 행렬 형태로 표현할 수 있다.
관측자의 속도에 따라 위 행렬의 좌표 변환이 이루어지는데, 행렬 원소들의 값이 서로 뒤엉키며 바뀌게 된다. 이 사실로부터, 전기장과 자기장이 근본적으로 분리할 수 없는 물리량이라는 것을 쉽게 추론할 수 있다.
전자기장의 에너지[편집]
정적인 장소에 있어서의 에너지[편집]
전하가 전하 밀도 ρ로 분포하고 있는 경우
또는
의 에너지를 저축할 수 있다.
이것들을 장소의 양으로 나타내면
에너지 밀도[편집]
로 정의되는 물리량이다.
전자기장이 가지는 에너지의 밀도를 나타내고 있어 전자기장이 외부에 일을 하지 않는 경우
의 연속의 방정식을 채운다. 여기서, S는 포인팅 벡터이다. 포인팅 벡터는 전자기장의 에너지의 흐름을 나타내고 있어 이 식은 전자장의 에너지가 보존하고 있는 것을 나타내고 있다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원