제임스 클러크 맥스웰

제임스 클러크 맥스웰(James Clerk Maxwell, FRS, 1831년 6월 13일 ~ 1879년 11월 5일)

제임스 클러크 맥스웰(James Clerk Maxwell, FRS, 1831년 6월 13일 ~ 1879년 11월 5일)은 스코틀랜드의 물리학자, 수학자이다

현대 인류 문명의 밑바탕이 된 전기문명의 근간인 전자기학을 정립한 위대한 물리학자로 평가받는다. 전자기학 뿐만 아니라 맥스웰-볼츠만 분포같이 열역학, 통계역학에도 큰 영향을 끼쳤다.

상세

제임스 클러크 맥스웰은 스코틀랜드의 에든버러에서 태어난 영국의 이론물리학자이자 수학자이다. 그의 가장 중요한 성과는 전기 및 자기 현상에 대한 통일적 기초를 마련한 것이다. 전기와 자기를 단일한 힘으로 통합한 전자기학은 뉴턴 역학과 함께 과학 발전의 초석이 되었다. 맥스웰의 전자기학의 확립은 19세기 물리학이 이룩한 성과로 높게 평가받고 있다. 수학에 뛰어났던 그가 기존에 존재했던 패러데이의 유도 법칙, 쿨롱의 법칙 등 전자기 이론을 수식적으로 정리하여 나타낸 식이 '맥스웰 방정식'이다. 이 방정식은 전자기학의 기초가 되는 미분 방정식으로 이는 볼츠만의 통계역학과 함께 19세기 물리학이 이룬 큰 성과로 높이 평가받고 있다.

맥스웰은 전기장과 자기장이 공간에서 빛의 속도로 전파되는 파동을 이룰 수 있음을 증명하였다. 맥스웰은 이를 바탕으로 연구를 계속하여 1864년 《전자기장에 관한 역학 이론》을 발표하여 빛이 전기와 자기에 의한 파동, 즉 전자파라는 것을 증명하였다. 맥스웰의 연구 성과는 전자기학의 성립에 큰 영향을 주었다.

그 외에도 맥스웰은 기체의 분자운동에 관한 연구에서 분자의 평균 속도 대신 분자의 속도 분포를 고려하여 속도 분포 법칙을 만들고 확률적 개념을 시사해 통계역학의 기초를 닦았다. 맥스웰의 전자기학 연구 성과와 기체 운동 연구는 이후 특수 상대성 이론과 양자 역학의 성립에 영향을 주었다.

맥스웰은 컬러 사진을 최초로 만든 사람이기도 하다. 맥스웰은 1861년 삼원색의 혼합으로 모든 색을 표현할 수 있다는 것을 응용하여 컬러 사진을 제작하였다.

맥스웰은 많은 물리학자들과 20세기 물리학에 무척 큰 영향을 끼친 19세기 과학자로 평가받고 있다. 맥스웰의 업적은 알베르트 아인슈타인이나 아이작 뉴턴과 견주어 지고 있다. BBC는, Physics World magazine이 2000년도를 맞아 100명의 지도급 물리학자들을 대상으로 투표를 하여 역사상 가장 큰 업적을 남긴 물리학자를 선정하였는데 아인슈타인과 뉴턴에 이어 맥스웰이 3위로 뽑혔다고 보도했다. 아인슈타인은 맥스웰 탄생 100주년을 기념하여 "그의 업적은 뉴턴 이후 가장 심원하고 풍성한 물리학의 성과"라고 평했다. 실제 아인슈타인은 자신의 연구실 벽에 뉴턴과 마이클 패러데이의 초상화와 함께 맥스웰의 사진을 걸어두었다고 한다.

생애

성장배경

맥스웰은 1831년 6월 13일 스코틀랜드 에든버러에서 부유한 중년층 가정의 외아들로 태어났다.그의 아버지 존 클러크 맥스웰(John Clerk Maxwell)은 변호사였고 어머니 프랜시스 케이 맥스웰(Francis Cay Maxwell)은 독실한 그리스도인이었다. 맥스웰의 아버지와 어머니 둘 다 재능있는 가문 출신이었으며, 맥스웰의 고조할아버지 존 클러크 경의 경우 스코틀랜드 재무성 관리이자 영국의 행정관료이며 훌륭한 작곡가였다. 또 고고학, 건축학, 역사학, 천문학 등 여러 분야에서 영향력있는 권위자였다. 맥스웰은 어릴적부터 조숙하고 머리가 뛰어난 것으로 알려져 있다. 어머니가 돌아가신 해인 1839년, 8살이었던 그는 성경의 시 119편을 암송했다는 일화도 있다. 이후 맥스웰은 가정교사에게 양육되었다. 일년 후 맥스웰은 더 높은 교육을 받기 위해 에든버러 아카데미에 들어가게 된다. 그는 어렸을 때부터 어머니에게 교육받은 덕분에 성서 지식이 뛰어났고 수학과 기하학을 쉽고 빠르게 터득해 친구들을 깜짝 놀라게 하기도 했다. 맥스웰은 곧 전 과목에서 우등하게 된다.

학창시절 - 첫 논문 발표

맥스웰이 14살일 때 그는 첫 번째 과학적 성과를 배출했다. 이는 바로 '난형곡선에 관한 논문'이다. 이는 핀과 끈과 연필을 사용해 한 장의 종이 위에 그릴 수 있는 곡선에 관한 논문이었다. 두 개의 핀을 고정한 후 끈을 이어 연필로 그릴 수 있는 곡선은 타원이다. 이때 끈의 길이를 조절하며 한 무리의 타원체를 생성할 수 있다는 것을 발견했고 그의 아버지가 아들의 성과를 그의 친구 제임스 포브스(James Forbes)에게 보여 주었다. 에든버러 대학교 교수였던 포브스는 맥스웰의 '이초점 타원체의 집합'을 에든버러 왕립학회에 발표했다. 이 논문은 대단한 관심을 불러일으켰고, 이를 계기로 맥스웰은 과학에 더욱 큰 관심을 가지고 공부하게 된다.

대학 생활 - 에든버러, 케임브리지 대학

맥스웰이 다녔던 에든버러 대학의 1827년 경의 모습(왼쪽), 트리니티 칼리지 재학시절의 맥스웰

1847년 맥스웰은 16살의 나이로 에든버러 대학에 입학하였다. 이 때만 해도 맥스웰은 수학과 과학에 재능을 보였지만 아버지의 의견에 따라 법학 분야로 진출할 생각을 가지고 있었다. 그러나 당시 에딘버러 대학 교수였던 제임스 포브스는 맥스웰이 과학을 전공해야 한다고 맥스웰의 아버지를 꾸준히 설득했고, 결국 1850년부터 맥스웰은 스코틀랜드를 떠나 과학 분야의 최고의 대학교 중 하나인 케임브리지 대학에서 공부하였다. 케임브리지 대학 내의 피터하우스 대학(Peterhouse College)에 입학했다가 곧 트리니티 대학으로 옮겼고 2학년 말에 장학생으로 선발되었다. 그는 이곳에서 뛰어난 물리학자들을 가르친 윌리엄 홉킨스(William Hopkins), 귀납 이론으로 유명한 철학자 윌리엄 휴얼, 유명한 영국의 수학자이자 물리학자인 스톡스 등의 영향을 받으면서 대학시절을 보냈다. 맥스웰이 수학하던 시절, 케임브리지 대학에는 수학 분야의 최고상 수상자를 결정하는 트라이퍼스라는 시험이 있었는데 이 시험의 출제 경향이 케임브리지 대학 학생들의 학문적 경향에 많은 영향을 끼쳤다. 트라이퍼스 시험은 물리학이 해석동역학 형태로 수학 교과 과정에 포함되어 있어, 케임브리지 수학자들은 기하학적이고 역학적인 도구를 사용하는 것을 선호했고 물리학자들 또한 전기동역학을 다루면서 해석학적 도구를 많이 사용했다. 맥스웰이 전자기학을 연구할 때도 이러한 학문적 경향이 드러났다. 맥스웰은 1854년 트라이퍼스 시험에서 차석을 했고, 이보다 좀 더 어려운, 스미스 상을 위한 시험에서 수석을 차지하며 케임브리지 대학을 졸업했다. 1855년, 그는 24살에 트리니티 대학의 학사 학위 학자로 머물면서 특별연구원으로 선발되어 전기와 자기에 대한 실험을 주관하였고 색채 이론에 관한 연구를 하였다.

킹스 대학 교수시절

서른여덟살 즈음 부인 캐서린과 함께

트리니티 대학의 특별연구원으로 선발되었지만, 맥스웰은 아버지의 건강이 악화되어 고향인 스코틀랜드로 돌아가 애버딘의 마셜 대학(Marischal College)의 자연철학 교수직을 맡게 된다. 당시 그는 많은 과학자들의 수수께끼였던 토성의 고리에 관해 관심을 가지고 있었다. 어떻게 토성의 고리가 유지될 수 있는지에 대해 2년을 연구한 맥스웰은, 1857년 토성의 고리의 구조에 관한 논문을 발표한다. 그는 토성의 고리가 작은 입자들로 이루어져야만 안정함을 보였고 그의 논문은 조지 에어리 경에게 '물리학에 대한 수학적 적용의 가장 훌륭한 예'라는 평가를 받았으며, 1859년 애덤스 상(Adams Prize)을 수상했다. 1980년대 미국의 우주선 보이저호에 의해 맥스웰의 예측은 옳다는 것이 증명되었다.

1858년 맥스웰은 마셜 칼리지 학장의 딸 캐서린 메어리 듀어(Katherine Mary Dewar)와 결혼하였다. 맥스웰 부부에 대한 기록은 많이 남아있지 않지만 맥스웰은 아내를 지극히 사랑하였고 서로에게 매우 헌신적이었던 것으로 알려져 있다. 자신의 건강이 나쁠 때에도 마찬가지였다. 맥스웰은 3주 동안 밤에는 아내의 침대 곁에 앉아 있고, 낮에는 연구소의 일을 돌본 적도 있다고 한다. 이후 그는 독일의 물리학자 루돌프 클라우지우스가 쓴 기체의 분산에 관한 논문을 읽고 기체분자의 운동에 관해 관심을 갖게 된다. 그는 맥스웰 분포라고 알려진 기체 분자 속력에 관한 식을 유도하였는데, 이는 통계역학의 시초로 여겨진다.

1860년 맥스웰은 킹스 칼리지 런던의 자연철학 및 천문학 교수로 취임했다. 그곳에서 전기와 자기에 대한 연구를 계속하였고 색 시각에 대한 연구로 런던 왕립학회의 럼퍼드 상(Rumford Medal)을 수상하였다.

케임브리지 교수 시절

1865년 맥스웰은 킹스 대학의 교수직을 사임하고 케임브리지 대학교의 교수가 되고 1871년에는 캐번디시 연구소에서 연구하였다. 그는 이후 캐번디시 연구소 사업에 전력을 기울였다. 또 맥스웰은 물리학이 진보하도록 돕고 학생 한 사람 한 사람이 자기 능력을 계발할 수 있게 돕는 일을 했다. 이는 캐번디시 연구소의 많은 연구원들이 다른 곳에 진출하여 보인 두드러진 모습을 통해 알 수 있다. 맥스웰의 가르침을 받은 학생 중 리처드 글레이즈브룩은 영국 국립 물리 연구소의 초대 소장이 됐고, 윌리엄 네이피어 쇼는 영국에서 기상학을 전문 수준으로 끌어올렸다. 제임스 부처는 변호사로서 성공하였고, 그외 많은 사람들이 대학 교수가 되었다. 1873년에는 아마 뉴턴의 <프린키피아> 이후 물리학 역사상 가장 잘 알려진 책이라고 할 수 있는 <전자기론>을 출판하였다. 이 논문에서 그는 자신의 전자기 이론의 또 다른 측면을 확장하여 설명했고, 4원수 개념을 전자기장 방정식에 도입하여 현대의 벡터 개념으로 표현하는 전자기장 방정식과 거의 닮은 모양으로 만들었다.

1874년에는 데번셔 공작이 맥스웰에게 그의 삼촌 헨리 캐번디시가 남긴 전기실험 작업의 미발표 자료를 남겨, 그것을 편집하는 것을 맡아 많은 시간을 할애했다. 맥스웰은 삶의 마지막 몇 해는 그 일을 하느라 소비하였다. 그 실험 자료에서 그는 쿨롱의 법칙을 쿨롱보다 효과적으로 증명하였다. 이 때 케임브리지에서의 맥스웰의 영향력은 그가 속한 학과를 넘어섰고, 또 유럽까지 뻗쳤다. 맥스웰은 1879년 11월 5일, 48세의 젊은 나이에 케임브리지에서 위암으로 생을 마감하였다.

업적

전자기학

먼저 맥스웰 이전에 물리학에서 전기와 자기는 따로 따로 그에 대한 이론이 존재했다. 전기에서는 전하 사이의 힘은 거리의 제곱에 반비례하고 전하량의 곱에 비례한다는 쿨롱의 법칙이, 자기에서는 비오-사바르 법칙이 있다. 두 법칙에서 실험적으로 계산된 상수 k1, k2에서, 이들의 비의 제곱근이 파동의 속력을 의미하고, 이것이 실험적으로 계산된 빛의 속력과 같았는데 이를 바탕으로 맥스웰은 ‘빛은 전자기파의 일종이다’라는 맥스웰의 빛의 전자기파설을 제안하게 된다.

맥스웰의 전자기 법칙은 전자기파가 빛의 속력으로 전기장과 자기장에 수직인 방향으로 진행한다는 것을 의미한다. 맥스웰의 전자기 방정식은 다른 사람의 손을 거쳐서 변형되었다. 열개가 넘었던 맥스웰의 방정식은 재능 있는 맥스웰의 후계자들에 의해 정리되었다.

맥스웰 방정식

맥스웰이 도달한 전자기장 방정식은 네 개의 식으로 이루어졌다.

1. $\oint _{S}^{\ }{E}\cdot {\hat {n}}dS\ ={{1} \over {\epsilon _{0}}}Q$
2. $\oint _{S}^{\ }{B}\cdot {\hat {n}}dS\ =0$
3. $\oint _{c}^{\ }{E}\cdot dl\ =-{{d} \over {dt}}\int _{S}^{\ }{B\cdot {\hat {n}}dS}$
4. $\oint _{c}^{\ }{B}\cdot dl\ ={\mu _{0}}I+{\mu _{0}}{\epsilon _{0}}{{d} \over {dt}}\int _{S}^{\ }{E\cdot {\hat {n}}dS}$

첫 번째 맥스웰 방정식은 가우스 법칙이며, 쿨롱의 법칙을 일반화 한 식이다. 전하를 둘러싼 임의의 폐곡면을 나가는 전기력선의 수는 폐곡면 내부의 알짜 전하에 의해 결정된다는 식이다. 두 번째 맥스웰 방정식 가우스 자기 법칙이며, 임의의 폐곡면을 통과하는 자기 선속이 0임을 의미하며, 이에 따라 N극 또는 S극이 따로 존재하는 이른바 자기 홀극은 존재하지 않는다. 세 번째 맥스웰 방정식은 패러데이의 유도 법칙이다. 자속 밀도의 시간에 따른 변화는 전기장을 생성한다는 내용의 식이다. 이 법칙은 임의의 폐경로를 따라 행한 전기장의 선적분인 기전력은 그 경로로 닫힌 임의의 면적을 통과하는 자기 선속의 변화율과 같다는 것을 의미한다. 네 번째 맥스웰 방정식은 변위 전류에 의해 수정된 앙페르 회로 법칙으로, 앙페르법칙이 일반화 된 식이고, 시간에 따라 변하는 전기장과 전류에 따라 변하는 전기장과 전류에 의한 자기장의 생성을 설명한다. 맥스웰은 에테르에 대한 가정으로 변위 전류에 대한 개념에 도달하였다.

이 방정식 속에 구현된 맥스웰의 장이론은 19세기 전자기 이론을 마무리지었고, 이 이론은 20세기까지 영향력을 발휘하였다. 아인슈타인은 맥스웰 방정식에서 공간과 시간의 개념을 과감하게 혁신할 실마리를 찾았고, 그 다음에 맥스웰의 전자기장 이론을 따라 자신의 일반 상대성 이론을 만들었다. 현대에 와서는 양자장론이 입자 물리학의 기둥이 되었다.

에테르 모형

전자기적 에테르의 개념은 맥스웰 방정식을 만드는데 매우 중요한 역할을 하였다. 전자기를 역학적으로 이해하기 위해 에테르라는 개념을 가정하였는데, 에테르는 광학적, 전자기적 효과를 전파시키는 매질이라고 믿어졌던 개념이다. 에테르를 통한 전자기파의 전파 모형은 그림과 같다.

모든 공간은 물질로 가득 차 있어 빈 곳이 없고 진공이 존재할 수 없는 공간이라고 믿었다. 에테르가 모든 공간에 퍼져있다고 생각했는데, 상호작용이 압력과 충격을 통해서만, 즉 어떤 매개 동인이나 물체의 실체적인 작용을 통해서만 일어날 수 있다고 생각하였다. 맥스웰은 전기장을 설명하면서 에테르를 제시하였다. 공간에 '유동'바퀴의 역할을 하는 작은 입자들이 층을 갖는 탄성 에테르가 존재하고, 도선에 전류가 흐르면 근접한 부분이 회전하고 이로 인해 에테르가 소용돌이를 형성한다. 회전하는 유동바퀴는 에테르의 다음 층으로 자신의 회전을 전달하고 첫 번째 층과 같은 방향으로 회전하는 소용돌이 고리의 두 번째 층을 형성한다. 유동 입자들의 초기 운동은 전기장과 연관이 있다. 이 효과는 일시적인 것이고 도선에 전류가 흐르기 시작한 후 잠시만 존재한다. 도선의 전류가 멈추면 일시적인 전기 변위가 발생하고, 초기 평형상태로 돌아가려는 에테르 때문에 반대방향으로 돌아간다. 도선 안의 전류가 일정하게 유지되면 전기 변위는 존재하지 않고, 소용돌이 필라멘트로 이루어진 자기장만 존재한다. 이는 패러데이의 유도 법칙을 설명해 준다.

기체의 분자 운동론

맥스웰의 주요 업적 중 하나는 기체 분자 운동론에 관한 것이다. 다니엘 베르누이가 제창한 이 이론은 많은 과학자들을 통해 발달했지만 특히 이 분야에서 수학자이자 실험가인 맥스웰이 막대한 발전을 시켰다. 1866년, 맥스웰은 기체 분자 운동을 통계적으로 공식화하였다. 맥스웰은 분자 분포 법칙을 정의하고 여러 가지 방법으로 기체 이론에 적용하였다. 이는 물리학에 통계 법칙을 제시한 최초의 논문 이었다.

맥스웰의 기체 분자 운동론은 기체 분자의 속도 분포를 다룬다. 그는 기체의 점성이 기체의 압력과 독립적이라고 예견했다. 맥스웰이 내린 결론은 기체가 서로 밀쳐 움직이는 무수한 분자로 구성돼 있다는 이론을 크게 발전시켰고, 이후 독일의 물리학자인 루트비히 볼츠만에 의해 분자들간의 에너지 분포를 나타낼 수 있도록 일반화되었다. 이것이 맥스웰-볼츠만 분포이다. 볼츠만은 맥스웰의 에너지 균등분배 원리를 일반화했다. 맥스웰-볼츠만 통계에 의하면 기체의 분포함수는 계의 전체 에너지(E), 기체의 절대 온도(T), 볼츠만 상수(k)와 비례 상수(C)로 표현되며, $f=Ce^{-{E}/{kT}}$가 된다. e는 자연 로그의 밑을 나타낸다. 제임스는 볼츠만의 연구결과를 다시 가져와 <물질의 관점에서 본 한 계의 에너지 평균 분포에 관한 볼츠만의 정리에 관해>라는 논문을 썼다. 제임스는 속도와 에너지 분포 이론을 새로운 방법으로 이끌어냈다. 이때 에너지 균등분배 원리가 자연스럽게 뒤따라오게 되었다.

색채이론

맥스웰의 빛깔 삼각형

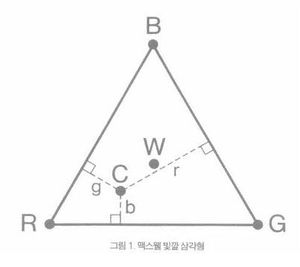
빛깔의 인지에 대한 관심은 에든버러 대학교 학생일 때부터 시작되었다. 그는 물감을 혼합하는 것처럼 색소를 혼합하는 것과 여러 색깔로 이루어진 디스크 판을 회전 시키는 것은 근본적인 차이가 있다는 것을 발견했다. 그는 색의 삼원색인 빨강, 노랑, 파랑대신 빛의 삼원색인 빨강, 초록, 파랑을 찾아냈고 색과 빛의 혼합을 감산혼합과 가산혼합으로 나누었다. 회전혼합을 실험하면서 맥스웰은 맥스웰의 빛깔 삼각형(Maxwell's colour triangle)을 발견했다.

열역학

열역학에도 상당한 기여를 하였다. 열역학에서 그의 이름이 들어가는 것만 해도 열역학 퍼텐셜 사이의 관계식인 맥스웰 관계식과 일반적인 입자의 속도 분포에 쓰이는 맥스웰-볼츠만 분포의 2가지가 있다. 특히 후자는 통계역학의 언어로 열역학을 설명하기 위한 매우 중요한 수단이다. 물론 실질적으로 완성한 것은 볼츠만이지만. 한편 1876년에 열역학 제2법칙을 작살내는 가상의 악마를 가정한 사고실험인 맥스웰의 악마를 고안하기도 했다.

맥스웰 관계식

열역학에서 절대온도(T), 압력(P), 부피(V), 엔트로피(S) 사이에 성립하는 관계식으로 '2계 편도함수의 대칭성'이 성립할 때 편미분 순서를 바꿀 수 있다는 정리(영의 정리)로부터 유도되는 관계식이다. 열역학에서 다루는 위 네 물리량의 관계식에는 특이점이 존재하지 않으므로[1] 기본적으로 영의 정리가 성립한다는 전제가 깔려있다.

맥스웰-볼츠만 분포

맥스웰 - 볼츠만 분포는 일원자 분자 이상기체의 속력에 대한 확률분포이며, 분자의 질량과 기체의 온도를 매개변수로 가진다. 이 분포를 통해 최빈속도, 평균속도, 제곱평균제곱근(root mean square) 속도(vrms)등을 계산할 수 있다. 이는 제임스 클러크 맥스웰이 처음 제안하였고, 이 업적을 접한 루트비히 볼츠만이 맥스웰의 가정을 바꾸어 다른 방식으로 증명였는데, 분자의 존재를 가정하고 있기 때문에 에른스트 마흐 등을 포함해 물질의 공간상에 연속적이라고 생각하는 당대 주류의 학파에 의해 인정받지 못했다. 그렇지만, 시간이 흐르면서 업적을 인정받게 되었고, 통계역학의 발전에도 큰 기여를 하였다. 또한, 후에 보스 - 아인슈타인 분포 와 페르미 - 디랙 분포의 발견에도 영향을 주었다.

맥스웰의 악마

1867년에 제임스 클러크 맥스웰이 고안한 사고실험과 그에 등장하는 주인공 악마. 맥스웰의 도깨비라는 이름으로도 많이 알려져 있다.

사고실험은 열역학의 엔트로피에 대한 것으로, 이 악마는 직관적으로 보면 특정 계의 엔트로피를 감소시킬 수 있어, 열역학 제2법칙을 무너뜨리는 역설적 존재이다. 그러나 그것은 정보 엔트로피를 간과했기 때문으로, 정보 엔트로피를 계산에 넣으면 이러한 악마가 실존하더라도 열역학 제2법칙을 위배하지는 않는다. 열역학적 엔트로피와 정보 엔트로피의 직접적인 연결 고리를 보여주는 사고실험이다.

평가

알베르트 아인슈타인은 맥스웰을 두고 다음과 같이 평했다.

"맥스웰 이전에 사람들은 물리적 실재를 물질의 점으로 생각했다. 그 변화는 운동만으로 구성되어 상미분방정식을 따르는 것이었다. 맥스웰 이후로 사람들은 물리적 실재가 연속적인 장으로 나타난다고 생각했는데, 이것은 역학적으로 설명할 수 없고 편미분 방정식을 따른다. 실재의 개념에 관한 이러한 변화는 뉴턴 이후 물리학의 가장 심대하고 가장 풍성한 수확이다.

"물리학은 맥스웰 이전과 이후로 나뉜다. 그와 더불어 과학의 한 시대가 끝나고 또 한 시대가 시작되었다."

맥스웰의 친구이자 그의 평전을 집필한 루이스 캠벨(Lewis Campbell)은 맥스웰에 대하여 다음과 같이 적었다.

"그(맥스웰)는 인간이 인식하는 주도적인 물리 법칙의 거대한 확실성을 줄이려고 끊임없이 노력했다. 마치 습관적으로 무한한 것들과 신비로운 교류를 하고 있는 것 같았다."

마이클 패러데이는 맥스웰에게 보낸 편지에서 다음과 같이 적었다.

"당신의 연구는 나에게 기쁨을 주었으며, 이 주제를 다룰 정도로 뛰어난 당신의 수학적 재능에 감탄했고, 그 다음에는 이 주제가 그렇게 정연한 것에 놀랐습니다."

주요 논문

• 1848년 <회전 곡선 이론에 관해>
• 1850년 <탄성 고체의 평형에 관해>
• 1855년 <눈으로 인지한 빛깔에 관한 실험>
• 1855년 <패러데이의 역선에 관해 1부>
• 1856년 <패러데이의 역선에 관해 2부>
• 1858년 <토성 고리의 운동의 안정성에 관해>
• 1860년 <기체의 역학적 이론에 관한 묘사> <혼합한 빛깔의 이론과 스펙트럼의 빛깔의 관계에 관해>
• 1861년 <물리적 역선에 관해 1, 2부>
• 1865년 <힘의 역비례 모양과 역비례 다이어그램에 관해>
• 1865년 <전자기장의 역학적 이론>
• 1866년 <공기와 다른 기체의 점도 또는 내적 마찰에 관해>
• 1867년 <기체의 역학적 이론에 관해>
• 1868년 <속도 조절기에 관해>
• 1870년 <언덕과 골짜기에 관해>
• 1871년 <<열이론>>
• 1873년 <<전기와 자기에 관한 논문집>>
• 1876년 <<물질과 운동>>
• 1879년 <물질의 관점에서 본 한 계의 에너지 평균 분포에 관한 볼츠만 정리에 관해>
• 1879년 <온도의 변동이 야기한 희박화 기체에서의 스트레스에 관해>
• 1879년 <<헨리 캐번디시 각하의 전기연구>>

참고자료

• 〈제임스 클러크 맥스웰〉, 《위키백과》
• 〈제임스 클러크 맥스웰〉, 《나무위키》
• 〈제임스 맥스웰〉, 《인물세계사》
• 〈맥스웰 관계식〉, 《나무위키》
• 〈맥스웰-볼츠만 분포〉, 《나무위키》
• 〈맥스웰의 악마〉, 《나무위키》

같이 보기

• 전자기학
• 전자기력
• 맥스웰 방정식
• 맥스웰-볼츠만 분포

이 문서는 인물사진 수정이 필요합니다.

이 제임스 클러크 맥스웰 문서는 산업혁명에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

산업 : 산업, 산업혁명 □■⊕, 기술, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지 산업혁명 가트너 하이퍼사이클 • 개량 • 개방 • 개선 • 개혁 • 교체 • 기술개발 • 기술발전 • 기술진보 • 기술혁명 • 대체 • 대체불가 • 발견 • 발명 • 발전 • 변모 • 변혁 • 변화 • 분업 • 분업화 • 산업 • 산업발전 • 산업혁명 • 산업화 • 융합 • 전파 • 정보혁명 • 진보 • 창의 • 창조 • 혁명 • 혁신 • 확대 • 확산 1차 산업혁명 (증기기관, 기계, 공장) 경공업 • 공업 • 공업화 • 공장 • 기계 • 기계업 • 기계화 • 러다이트 운동 • 면직물 • 방적기 • 방직기 • 석유 • 석탄 • 섬유 • 섬유업 • 수공업 • 원유 • 정유업 • 제강업 • 제조 • 제조업 • 제철업 • 중공업 • 증기기관 • 철강 • 철강업 • 화학공업 2차 산업혁명 (전기, 전자) 가전제품 • 내연기관 • 냉장고 • 대량생산 • 라디오 • 모터 • 발전 • 발전기 • 발전소 • 선풍기 • 세탁기 • 에어컨 • 오디오 • 원자 • 음향기기 • 전구 • 전기 • 전기공학 • 전기밥솥 • 전기전자 • 전기전자제품 • 전기제품 • 전등 • 전력 • 전력업 • 전류 • 전선 • 전자 • 전자계산기 • 전자공학 • 전자제품 • 전축 • 전화 • 전화기 • 조명기기 • 철도 • 축음기 • 카세트 • 텔레비전 3차 산업혁명 (컴퓨터, 인터넷) ICT • IT • PC • SNS • 개발자 • 검색 • 구글 • 네이버 • 네트워크 • 노트북 • 데스크탑 • 데이터 • 디지털 • 디지털화 • 마이크로소프트 • 메신저 • 모니터 • 모바일 • 모바일기기 • 반도체 • 서버 • 소프트웨어 • 슈퍼컴퓨터 • 스마트폰 • 아날로그 • 아마존 • 애플 • 야후 • ㈜엔씨소프트 • 와이파이 • 웹 • 웹브라우저 • 웹사이트 • 유튜브 • 이메일 • 인터넷 • 인터넷게임 • 인터넷뱅킹 • 인터넷쇼핑 • 전산 • 전산실 • 전산화 • 정보 • 정보격차 • 정보기술 • 정보사회 • 정보통신 • 정보통신기술 • 정보화 • 진공관 • 카카오 • 컴퓨터 • 코딩 • 통신 • 페이스북 • 포털 • 프로그래머 • 프로그래밍 • 프로그램 • 프린터 • 하드웨어 • 홈페이지 • 휴대폰 4차 산업혁명 (인공지능, 모빌리티) 3D 프린팅 • 4차 산업혁명 • 5G • 가상현실 • 드론 • 로봇 • 로봇 프로세스 자동화(RPA) • 메타버스 • 모빌리티 • 배터리 • 블록체인 • 빅데이터 • 사물배터리 • 사물인터넷 • 생성형 AI • 생체인식기술 • 수소경제 • 스마트공장(스마트팩토리) • 스마트시티 • 스마트팜 • 스마트 헬스케어 • 스마트홈 • 양자컴퓨터 • 엣지컴퓨팅 • 인공지능 • 인공지능 로봇 • 자율주행 • 자율주행 자동차 • 전기자동차 • 증강현실 • 클라우드 • 테슬라 • 푸드테크 • 핀테크 • 하이퍼루프 • 혼합현실 주요 인물 니콜라 테슬라 • 데니스 리치 • 래리 페이지 • 리누스 토르발스 • 마이클 패러데이 • 마크 저커버그 • 빌 게이츠 • 세르게이 브린 • 스티브 잡스 • 앤드루 카네기 • 윌리스 캐리어 • 일론 머스크 • 제임스 클러크 맥스웰 • 제임스 와트 • 제프 베조스 • 존 데이비슨 록펠러 • 콜린 클라크 • 토머스 에디슨 • 팀 버너스-리 기관 • 단체 • 전략 국가기반시설 디지털화(SOC 디지털화) • 국회 4차산업혁명포럼 • 그린 뉴딜 • 디지털 뉴딜 • 디지털 인프라 • 비대면 산업 • 세계4차산업혁명협의회 • 한국판 뉴딜 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반