"자료구조"의 두 판 사이의 차이
(→그래프의 탐색) |
(→비선형 구조) |
||
| 72번째 줄: | 72번째 줄: | ||
====== 입/출력 방식 ====== | ====== 입/출력 방식 ====== | ||
[[파일:덱_입출력.png]]<ref name='deque'></ref><br> | [[파일:덱_입출력.png]]<ref name='deque'></ref><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== 파일 구조 === | === 파일 구조 === | ||
2020년 8월 11일 (화) 16:35 판
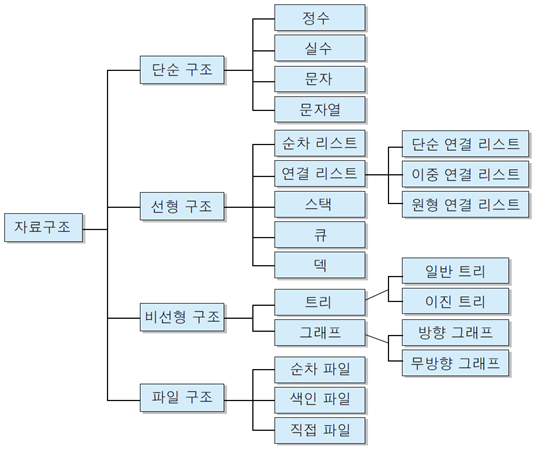
자료구조(資料構造, data structure)란, 자료의 집합을 의미하며 각 원소들 사이의 관계가 논리적으로 정의된 일정한 규칙에 의하여 나열되며 자료에 대한 처리를 효율적으로 수행할 수 있도록 자료를 조직적, 체계적으로 구분하여 표현한 것을 말한다. [1]
목차
개요
자료구조는 컴퓨터 과학에서 효율적인 접근 및 수정을 가능케 하는 자료의 조직, 관리, 저장을 의미한다. 더 정확히 말해, 자료 구조는 데이터 값의 모임, 또 데이터 간의 관계, 그리고 데이터에 적용할 수 있는 함수나 명령을 의미한다. 신중히 선택한 자료구조는 보다 효율적인 알고리즘을 사용할 수 있게 한다. 이러한 자료구조의 선택문제는 대개 추상 자료형의 선택으로부터 시작하는 경우가 많다. 효과적으로 설계된 자료구조는 실행시간 혹은 메모리 용량과 같은 자원을 최소한으로 사용하면서 연산을 수행하도록 해준다. 자료구조에는 여러 종류가 있으며, 이러한 각각의 자료구조는 각자의 연산 및 목적에 맞추어져 있다. 예를 들어 B-트리는 데이터베이스에 효율적이며, 라우팅 테이블은 네트워크(인터넷, 인트라넷)에 일반적이다. 다양한 프로그램을 설계할 때, 어떠한 자료구조를 선택할지는 가장 우선적으로 고려되어야 한다. 이는 큰 시스템을 제작할 때 구현의 난이도나 최종 결과물의 성능이 자료구조에 크게 의존한다는 것을 많은 경험이 뒷받침하기 때문이다. 일단 자료구조가 선택되면 적용할 알고리즘은 상대적으로 명확해지기 마련이다. 때로는 반대 순서로 정해지기도 하는데, 이는 목표로 하는 연산이 특정한 알고리즘을 반드시 필요로 하며, 해당 알고리즘은 특정 자료구조에서 가장 나은 성능을 발휘할 때와 같은 경우이다. 어떠한 경우든, 적절한 자료구조의 선택은 필수적이다. 이러한 관점은 알고리즘보다 자료구조가 보다 중요한 요소로 적용되는 많은 정형화된 개발론 그리고 프로그래밍 언어의 개발을 촉발시켰다. 대부분의 언어는 일정 수준의 모듈개념을 가지고 있으며, 이는 자료구조가 검증된 구현은 감춘 채 인터페이스만을 이용하여 다양한 프로그램에서 사용되는 것을 가능하게 해준다. C++, 자바와 같은 객체지향 프로그래밍 언어는 특별히 이러한 목적으로 객체를 사용한다. 이러한 자료구조의 중요성으로 말미암아, 최근의 프로그래밍 언어 및 개발 환경은 다양한 표준 라이브러리를 제공하고 있다. 예로, C++의 표준 템플릿 라이브러리나 자바의 자바 API, 마이크로소프트 .NET과 같은 것들을 들 수 있다. 자료구조에서 가장 기초적인 단위는 행렬, 레코드, 유니온, 참조와 같은 것이다. 예를 들어, Nullable 참조는 참조와 유니온의 조합으로 나타낼 수 있으며, 가장 단순한 자료구조 가운데 하나인 연결 리스트는 레코드와 Nullable 참조로 나타낼 수 있다.[2]
특징
- 효율성(Efficiency)[1]
상황에 맞는 알고리즘을 사용하여 자료를 구조화 시키기 때문에 효율적으로 동작한다.
예를 들어 모든 사원에 대해 사번과 이름의 쌍을 배열이라는 자료구조로 만들었을 때 사번을 가지고 이름을 찾을 경우 배열은 인덱스를 이용하여 데이터를 저장하기 때문에 찾으려는 사번이 첫번째 인덱스에 저장되어 있을 경우 한번의 검색으로 찾을 수 있지만 최악의 경우 제일 마지막 인덱스에 위치할 수 있으므로 데이터의 수만큼 검색을 해야 한다.
평균적으로 자료수/2 만큼의 검색을 해야 하므로 데이터를 찾는 작업이 빈번하고 데이터가 많을 경우 그다지 효율적이지 못하다. 이럴 때에는 해시 테이블과 같은 자료구조를 이용하여 좀 더 빠르게 검색 작업을 할 수 있다.
이처럼 상황에 맞는 적절한 자료구조를 이용하게 되면 데이터 처리의 효율을 높일 수 있다.
- 추상화(Abstraction)[1]
추상화란 복잡한 자료, 모듈, 시스템 등으로부터 핵심적인 개념 또는 기능을 간추려내는 것을 말한다.
자료구조를 이용하여 데이터를 처리할 경우 처리할 데이터를 어떻게 삽입하고 어떻게 추출할 것인가에 중점을 두지 않는다. 즉, 자료구조 자체를 구현하는 알고리즘에 중점을 두지 않고 어느 시점에 데이터를 삽입할 것이며 어느 시점에 데이터를 추출하고 이러한 데이터를 어떻게 사용할 것인지에 초점을 맞출 수 있기 때문에 프로그램의 비즈니스적인 요소에 좀 더 시간을 할애할 수 있다.
데이터를 처리하는 관점에서 보면 특정 자료구조 자체의 내부 구현은 그리 중요하지 않기 때문에 어떻게 구현했는지 보다 어떻게 사용하는지에 대해서 알고 있으면 된다.
예를 들어 스택(Stack)의 경우 가장 마지막에 삽입한 데이터를 가장 먼저 꺼내는 자료구조이고 push(), pop() 메소드를 통해서 데이터를 삽입하고 꺼낼 수 있다.
그리고 이러한 자료구조의 추상화는 실제 구현한 언어가 무엇인지에 따라 실제 그 코드는 다르지만 추상적인 개념에 대해서만 알고 있으면 되기 때문에 언어에 종속적이지 않다는 특징을 가진다.
- 재사용성(Reusability)[1]
자료구조를 이용하여 데이터를 처리할 경우 해당 자료구조의 인터페이스만 이용하여 데이터를 처리하도록 하므로 모듈화가 가능하다. 이는 자료구조를 설계할 때 특정 프로그램에 맞추어 설계하지 않고 다양한 프로그램에서 사용될 수 있도록 범용화하여 설계함으로써 가능하다.
분류
선형 구조
- 선형 구조 : 데이터가 연속적으로 연결되어 있는 모양으로 구성하는 방법이다.
배열과 같이 연속되는 기억장소에 저장되는 리스트이며, 포인터 등을 사용하여 자료를 연결하면 그 결과가 자료에 일직선상에 표시되거나 하나의 원상에 표시되는 구조이다.
선형 리스트(Linear List)
- 선형 리스트(Linear List) : 배열과 같이 연속되는 기억장소에 저장되는 리스트이다.
장단점
- 장점
저장 효율이 뛰어나고 접근 속도가 빠르며 간단한 자료 구조이다.[3]
- 단점
삽입, 삭제가 어렵다. (끝값은 쉽지만 중간값을 삽입, 삭제 시 그 이후의 값을 전부 복사 후 처리해야 한다.)[3]
연결 리스트(Linked List)
- 연결 리스트(Linked List) : 자료들을 반드시 연속적으로 배열시키지는 않고 임의의 기억공간에 기억시키되, 자료 항목의 순서에 따라 노드의 포인터 부분을 이용하여 서로 연결시킨 자료 구조이다.[4]
장단점
- 장점
링크로써 구현되어있기 때문에, 자료를 추가하거나 삭제할 시에 링크만 바꿔주면 되기 때문에 추가, 삭제가 용이하다.(추가 원소 이동 연산이 불필요하다.)
메모리 효율성이 우수하다.
필요할 때마다 데이터 추가, 삭제할 수 있기 때문에 배열 리스트처럼 최대 원소 개수 지정이 필요 없다.[5]
- 단점
원하는 원소를 찾을 때까지 포인터로 노드를 탐색해야 하기 때문에 탐색 연산의 비용이 높고 구현이 어렵다.[5]
단순 연결 리스트
이중 연결 리스트
원형 연결 리스트
스택(Stack)
- 스택(Stack) : 후입선출(後入先出, Last In First Out; LIFO)의 자료구조이다. 데이터 저장소에서 새로 들어오는 데이터의 위치가 저장소의 끝 부분(Top 혹은 Top pointer라고 한다)이고, 써먹기 위해 내보내는 데이터 역시 저장소의 끄트머리에서 나간다. 입력은 push, 출력은 pop이다. peek는 Top의 위치에 있는 데이터를 확인하는 것을 말한다.[6]
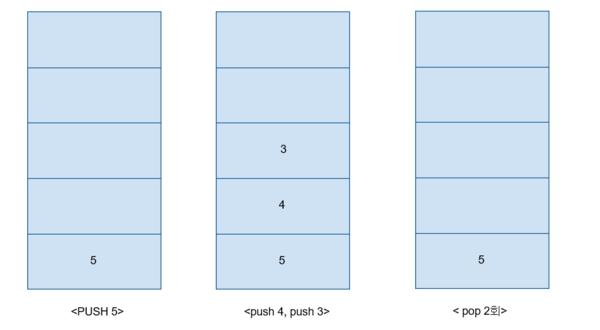
입/출력 방식
 [7]
[7]
1. 가장 먼저 5를 PUSH 한다. 스택 자료 구조에 가장 아래에 위치하게 된다.
2. 차례대로 PUSH 4, PUSH 3을 한 결과이다.
3. POP 2회를 실시하게 되면 출력 결과는 3,4가 된다. 즉 3은 가장 나중에 입력 되었지만 가장 먼저 출력이 된다.[7]
큐(Queue)
- 큐(Queue) : 선형 리스트의 한쪽에서는 삽입, 다른 한쪽에서는 삭제 작업이 이루어지도록 구성한 자료구조이다.
- 가장 먼저 삽입된 자료가 가장 먼저 삭제되는 선입선출(FIFO : First In First Out) 구조이다.[8]
선형 큐(Linear Queue)
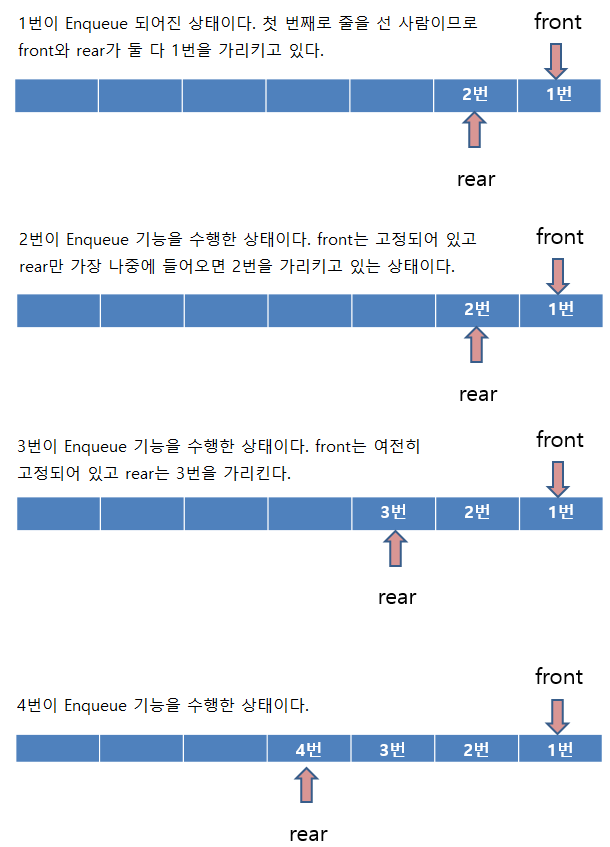
- 선형 큐(Linear Queue) : 선형 큐는 데이터를 집어넣는 Enqueue 기능과 데이터를 내보내는 Dequeue 기능을 제공한다.[9]
입력(Enqueue)
출력(Dequeue)
원형 큐(Circular Queue)
- 원형 큐(Circular Queue) : 원형 큐는 선형 큐의 문제점을 보완하기 위한 자료구조이다. 선형큐의 문제점은 rear이 가리키는 포인터가 배열의 마지막 인덱스를 가리키고 있을 때 앞쪽에서 Dequeue로 발생한 배열의 빈 공간을 활용할 수 없는데, 원형큐에서는 포인터 증가 방식이 (rear+1)%arraysize 형식으로 변환하기 때문에 배열의 첫 인덱스부터 다시 데이터의 삽입이 가능해진다.[10]
입력(Enqueue)
rear값을 1 증가시키면서 해당 인덱스에 데이터를 삽입시킨다. 이때, (rear+1) % array.length 조건을 통해서 원형큐가 꽉찬 상태인지 확인한다. 예를들어, 큐의 사이즈는 4이고 enqueue(1),enqueue(2),enqueue(3)을 수행하고 euqueue(4)를 수행하면 (3+1) % 4 == front 이므로 enqueue를 수행할 수 없다.[11]
출력(Dequeue)
front의 포인터를 1 증가시면서 데이터를 제거한다.[11]
덱(Deque)
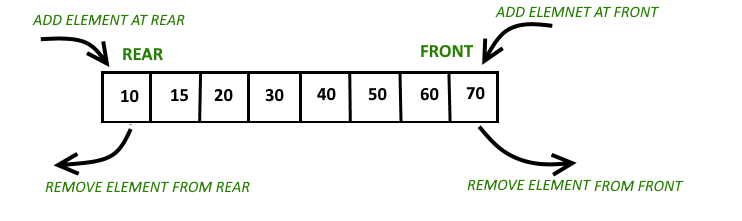
- 덱(Deque) : Double-ended queue의 약자로, 양 끝에서만 데이터를 넣고 양 끝에서 뺄 수 있는 자료구조이다. 큐는 push, pop을 할 수 있는 위치가 한 방향으로 고정되어 있지만, 덱은 앞에서도 push, pop, 뒤에서도 push, pop이 모두 가능하다.[12]
입/출력 방식
파일 구조
순차 파일
색인 파일
직접 파일
각주
- ↑ 1.0 1.1 1.2 1.3 islove8587, 〈자료구조란 〉, 2015년 11월 24일
- ↑ 위키백과, 〈자료구조 〉
- ↑ 3.0 3.1 S.Zinlee,〈선형 리스트와 연결 리스트 〉, 2011년 8월 12일
- ↑ 코딩팩토리,〈[1]〉, 2018년 8월 22일
- ↑ 5.0 5.1 요시,〈배열 리스트와 연결 리스트의 차이 (장단점)〉, 2017년 7월 19일
- ↑ 나무위키,〈스택(자료구조)〉
- ↑ 7.0 7.1 Lkt_Programmer,〈스택(Stack) 자료 구조 〉, 2017년 9월 28일
- ↑ Mr.lee,〈자료 구조의 개념 정리〉, 2019년 9월 10일
- ↑ 9.0 9.1 9.2 Lkt_Programmer,〈선형 큐(Linear Queue) 자료 구조〉, 2017년 9월 29일
- ↑ Lkt_Programmer,〈원형 큐 (Circular Queue) 자료 구조〉, 2017년 10월 13일
- ↑ 11.0 11.1 syunyun,〈원형 큐〉, 2019년 12월 20일
- ↑ 12.0 12.1 ldgeao99,〈자료구조 덱〉, 2019년 4월 23일
참고자료
같이 보기

 위키원
위키원