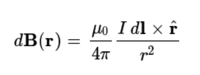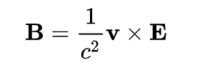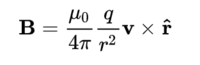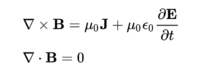"자기장"의 두 판 사이의 차이
잔글 (→같이 보기) |
|||
| (다른 사용자 한 명의 중간 판 2개는 보이지 않습니다) | |||
| 15번째 줄: | 15번째 줄: | ||
전류가 흐르는 도선의 주위에 나침반을 가져가면 나침반의 바늘이 도선을 중심으로 동심원을 그리며 정렬하는 것을 관측할 수 있다. 이것은 전류가 흐르는 도선 주위에 동심원 방향의 자기장이 생긴다는 것을 알려준다. 전류가 흐르는 도선 주위에 형성되는 자기장은 [[비오·사바르의 법칙]]을 이용하여 구할 수 있다. 그림 2에서처럼, 전류 ''i''가 흐르는 회로에서 원점에 놓인 아주 작은 전류 요소 ''idI''이 '''r'''만큼 떨어진 곳에 만드는 자기장 '''''d''B(r)'''을 수식으로 나타내면, | 전류가 흐르는 도선의 주위에 나침반을 가져가면 나침반의 바늘이 도선을 중심으로 동심원을 그리며 정렬하는 것을 관측할 수 있다. 이것은 전류가 흐르는 도선 주위에 동심원 방향의 자기장이 생긴다는 것을 알려준다. 전류가 흐르는 도선 주위에 형성되는 자기장은 [[비오·사바르의 법칙]]을 이용하여 구할 수 있다. 그림 2에서처럼, 전류 ''i''가 흐르는 회로에서 원점에 놓인 아주 작은 전류 요소 ''idI''이 '''r'''만큼 떨어진 곳에 만드는 자기장 '''''d''B(r)'''을 수식으로 나타내면, | ||
| − | [파일:DBr.png|썸네일|200픽셀|가운데|]] | + | |
| + | [[파일:DBr.png|썸네일|200픽셀|가운데|]] | ||
이 된다는 것이 비오·사바르의 법칙이다. 즉, 전류가 흐르는 도선이 만드는 자기장의 크기는 전류의 크기에 비례하고 전류로부터의 거리의 제곱에 반비례하며, 그 방향은 도선을 오른손으로 감쌀 때 네 손가락의 방향이 된다. 여기서 ''μ₀''은 진공의 투자율이고, r^='''r'''/''r''은 '''r'''방향의 단위벡터이다. 이 작은 전류 요소에 의한 자기장을 전체 도선에 대하여 선적분하면 전체 도선에 흐르는 전류에 의한 자기장 '''B'''를 구할 수 있다. | 이 된다는 것이 비오·사바르의 법칙이다. 즉, 전류가 흐르는 도선이 만드는 자기장의 크기는 전류의 크기에 비례하고 전류로부터의 거리의 제곱에 반비례하며, 그 방향은 도선을 오른손으로 감쌀 때 네 손가락의 방향이 된다. 여기서 ''μ₀''은 진공의 투자율이고, r^='''r'''/''r''은 '''r'''방향의 단위벡터이다. 이 작은 전류 요소에 의한 자기장을 전체 도선에 대하여 선적분하면 전체 도선에 흐르는 전류에 의한 자기장 '''B'''를 구할 수 있다. | ||
| 28번째 줄: | 29번째 줄: | ||
자석과 자기가 훨씬 더 이전에 알려져 있었음에도 자기장에 대한 연구는 1269년 프랑스의 학자 페트루스 페레그리누스(Petrus Peregrinus de Maricourt)가 철 바늘을 이용하여 구 모양의 자석 표면에 자기장을 배치시키면서 시작되었다. | 자석과 자기가 훨씬 더 이전에 알려져 있었음에도 자기장에 대한 연구는 1269년 프랑스의 학자 페트루스 페레그리누스(Petrus Peregrinus de Maricourt)가 철 바늘을 이용하여 구 모양의 자석 표면에 자기장을 배치시키면서 시작되었다. | ||
| + | == 표현 == | ||
| + | === 자기력선 === | ||
| + | 자기력선(magnetic lines of force)이란 자기장이 뿜어 나오는 모습을 형상화한 일련의 선들이다. 자기장의 방향은 자기력선의 접선의 방향과 같고, 자기장의 세기는 자기력선의 밀도에 비례한다. 자기 홀극이 존재하지 않으므로, 자기력선은 절대로 끊어지지 않는다. | ||
| + | |||
| + | 비록 우리가 자기력선을 그릴 때는 화살표 모양으로 그리지만, 그 화살표는 어떠한 실제 운동이나 흐름을 묘사하는 것이 아님을 명심해야 한다. 이는 자기장이 벡터가 아니라는 사실과 관련되어 있다. 엄밀히 말해서 자기장은 벡터가 아니라 유사벡터이다. 이 구분은 대칭성을 이용해 자기장 문제를 분석할 때 중요한데, '''B'''가 두 벡터의 벡터곱과 관련되어 있다는 사실(로런츠 힘)로부터 알 수 있다. | ||
| + | |||
| + | === 극에 대한 오해 === | ||
| + | 나침반에 써있는 N극과 S극은 지구 자기장의 N극과 S극을 가리키는 것이 아니라 그 반대를 가리킨다. | ||
| + | |||
| + | 나침반에 써있는 N극은 지구의 N극이 아니라 북쪽(North)을 가리키게 설계되어 있다. 즉, 자석의 "N극"은 엄밀히 말해 "북극을 향하는 극(north-seeking pole)"이다. 따라서 지구의 남극은 N극이고 북극은 S극이 된다. 자기력선은 자석의 N극에서 나와 S극으로 들어가므로, 실제 지구의 자기력선은 남극에서 나와 북극으로 들어가게 된다. | ||
| + | |||
| + | 이렇게 주어진 극에 대한 약속은 비오-사바르 법칙에 나오는 부호 약속, 전하의 부호 약속 등과 마찬가지로 관습적이다. | ||
| + | |||
| + | == 자기장의 생성 == | ||
| + | === 점전하가 만드는 자기장 === | ||
| + | 총 자기장은 각각의 전하가 만드는 자기장의 합으로 계산할 수 있다. 점전하가 만드는 자기장은 다음과 같다. | ||
| + | |||
| + | [[파일:점전하 자기장.png|썸네일|200픽셀|가운데|]] | ||
| + | |||
| + | 만약 전하가 일정한 속도로 움직이고 있다면, 비오-사바르 법칙을 통해 이 식을 다음과 같이 전개할 수 있다. | ||
| + | |||
| + | [[파일:전하가 일정한 속도 시 자기장.png|썸네일|200픽셀|가운데|]] | ||
| + | |||
| + | * ''q''는 자기장을 만드는 [[점전하]]의 전하량으로, 단위는 [[쿨롱]]이다. | ||
| + | * ''v''는 전하 ''q''의 속도벡터로, 단위는 미터 매 초이다. | ||
| + | * '''B'''는 자기장으로, 단위는 테슬라이다. | ||
| + | |||
| + | === 벡터 미적분학으로의 표현 === | ||
| + | 벡터 미적분학을 사용하면 자기장의 생성과정을 수학적으로 간단하고 아름답게 표현할 수 있다. 진공에서, | ||
| + | |||
| + | [[파일:벡터 미적분학.png|썸네일|200픽셀|가운데|]] | ||
| + | |||
| + | * '''∇×'''는 회전 연산자이다. | ||
| + | * '''∇∙'''는 발산 연산자이다. | ||
| + | * '''''μ₀'''''는 진공의 투자율이다. | ||
| + | * '''J'''는 전류밀도이다. | ||
| + | * '''∂'''는 편미분 연산자이다. | ||
| + | * '''Ⲉ₀'''는 진공의 유전율이다. | ||
| + | * '''E'''는 전기장을 의미한다. | ||
| + | * '''''t'''''는 시간이다. | ||
| + | |||
| + | 첫 번째 방정식은 앙페르 회로 법칙으로 알려진 법칙을 맥스웰이 수정한 것이다. 이 식의 두 번째 항이 바로 맥스웰이 수정한 부분인데, 정적 계(static system)나 준정적 계(quasi-static system)에서는 0이 되어 앙페르의 회로법칙과 일치하게 된다. 두 번째 방정식은 자기홀극이 존재하지 않음을 수학적으로 나타낸 식이다. 이들은 맥스웰 방정식에 포함되며, 여기서 사용된 표기법은 올리버 헤비사이드가 사용한 것이다. | ||
| + | |||
| + | == 자기장과 상대성 이론 == | ||
| + | 맥스웰은 자신의 네 가지 방정식을 통해 전기와 자기를 합치는 데 많은 공헌을 했다. 하지만 맥스웰이 만든 체계에서도 전기와 자기는 각각 독립적인 다른 현상으로 존재한다. 하지만 실제로 전기장과 자기장은 전자기 (2차) 텐서라는 한 대상의 두 가지 모습으로, 알베르트 아인슈타인이 특수 상대성 이론을 사용하여 이를 입증했다. 이 이론에 따르면 한 관성계에 있는 관찰자가 자기력을 느낄 때 다른 관성계에 존재하는 관찰자는 [[전기력]]을 느낄 수도 있는 것이다. 따라서, [[특수상대성이론]]을 적용하면 자기력은 운동하는 전하의 전기력에 불과함을 보일 수 있고, (특정 관찰자에 대해 상대적인) 운동과 정전기력에 대한 지식으로부터 자기력의 성질을 예측하는 것도 가능하다. | ||
| + | |||
| + | 이것을 증명할 수 있는 쉬운 사고실험으로, 무한하고 평행한 두 개의 동일한 도선을 생각해보자. 두 도선에는 동일한 전하가 흐르고 있고, 이들은 서로에 대해 정지해 있으면서 동시에 관찰자 A에 대해서는 동일한 속도로 운동하고 있다. 여기서 두 도선 근처에서 도선과 동일한 속도로 운동하고 있는 또 다른 관찰자 B를 도입하자. 그리고 B가 도선 사이에 척력으로 작용하는 정전기력과 그에 따른 가속도를 측정했다고 하자. A가 측정할 때는 두 도선이 자신에 대해 일정한 속도로 운동하고 있으므로 길이 수축이 일어나게 되고, 이에 따라 두 도선 사이에 작용하는 가속도가 B가 측정한 가속도에 비해 작게 측정될 것이다. 이 감소한 가속도는 인력으로 보이게 되고, 이 인력은 고전전자기학에서 정전기력을 감소시키고 속도가 증가함에 따라 같이 증가하는 항에 해당한다. 이 가상적 힘의 크기는 고전전자기학에서 말하는 [[전자기력]]과 정확히 일치한다. | ||
| + | |||
| + | == 응용 == | ||
| + | 자기장을 변화시키면 패러데이 전자기 유도 법칙에 의해 전기장과 전류를 유도할 수 있다. 이 전류는 고정된 자기장 속을 운동하는 도체에서도 유도될 수 있다. 이 현상이 바로 [[발전기]]와 [[전동기]]의 원리다. | ||
| + | |||
| + | === 회전 자기장 === | ||
| + | 회전 자기장은 극성을 갖고 비상대론적인 속력으로 회전하는 자기장을 가리킨다. 회전 자기장 안에 있는 영구자석은 외부장에 대해 자세를 유지하려고 한다. 이 현상이 바로 교류전동기의 핵심 작동원리다. [[삼상교류]] 혹은 더 높은 다상교류를 사용하면 좋은 회전 자기장을 얻을 수 있다. 동기전동기와 유도전동기는 고정자의 회전 자기장을 이용해 회전자를 움직인다. | ||
| + | |||
| + | 1882년, 니콜라 테슬라는 처음으로 회전 자기장의 개념을 창안했고, 1885년에는 갈릴레오 페라리스(Galileo Ferraris)에 의해 독립적으로 회전 자기장의 개념이 연구되었다. 1888년, 테슬라는 자신의 작업을 통해 미국특허 381968번을 취득했고 같은 해 페라리스는 자신의 연구업적을 토리노의 왕립아카데미에 논문으로 제출했다. | ||
| + | |||
| + | === 자기장 균열 === | ||
| + | 최근 태양 주변의 폭발로 인해 지구를 보호하는 자기장 내에 큰 규모의 균열이 발견됐다. 2008년 여름, 두께가 6400km에 이르는 입자층이 지구 대기 바깥에서 관측됐으며 이는 그간 관측된 자기장 균열 규모 가운데 가장 크다고 버클리대 마릿 오이로셋 교수 등이 밝혔다. | ||
| + | |||
| + | == 동영상 == | ||
| + | <youtube> ozmlC1ewRAw&t=4s </youtube> | ||
== 참고자료 == | == 참고자료 == | ||
| − | * 〈[ | + | * 〈[https://ko.wikipedia.org/wiki/%EC%9E%90%EA%B8%B0%EC%9E%A5 자기장]〉, 《위키백과》 |
| − | * 〈[ | + | * 〈[https://terms.naver.com/entry.naver?docId=4389642&cid=60217&categoryId=60217 자기장]〉, 《물리학백과》 |
| − | |||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[자기 (물리)|자기]] | ||
| + | * [[장 (물리)|장]] | ||
* [[전자기장]] | * [[전자기장]] | ||
* [[자석]] | * [[자석]] | ||
| − | |||
* [[자기력]] | * [[자기력]] | ||
| − | {{ | + | {{전기|검토 필요}} |
2024년 4월 20일 (토) 12:19 기준 최신판
자기장(磁氣場, magnetic field)이란 자석이나 전류에 의해 자기력이 작용하는 공간, 자기력을 매개하는 벡터장이다. 고전적으로는 움직이는 전하, 즉 전류에 의하여 발생하나, 양자역학에서는 입자 고유의 스핀도 전류와 같은 역할을 할 수 있다. (이에 따라 강자성체가 영구자성을 가질 수 있다.) 자기장의 방향은 자기장 안에 있는 나침반이 가리키는 방향과 같다. 또한 자기장의 방향을 연속적으로 이은 선의 간격이 촘촘할수록 자기장의 세기가 세다.
목차
개요[편집]
막대자석 또는 전류가 흐르는 도선 주위에 나침반을 가까이 가져가면 나침반의 바늘이 힘을 받아 돌아가는 것을 쉽게 관측할 수 있다. 이것은 자석 또는 전류가 흐르는 도선 주위에 자기력이 작용하는 장(field)이 형성되기 때문이다. 자기력을 받아 움직이는 전하 또는 자기모멘트가 그 위치에 따라 받는 자기력이 달라지는 것을 나타내기 위해서, 질량을 가진 물질에 의한 중력장 또는 전하 주위에 형성되는 전기장과 유사한 방법으로, 자기장이라는 물리량을 정의한다.
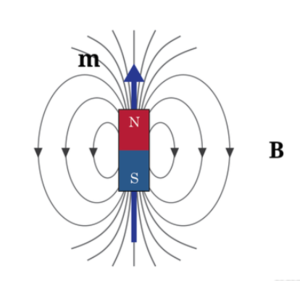
자기장을 시각적으로 표현하기 위하여 자기력선을 이용한다. 자기력선은 자기장 안에 놓인 나침반 바늘의 N극이 가리키는 방향으로 짥은 화살표를 그려넣고, 이 화살표를 끊어짐 없이 연결하여 그린 연속선이다. 따라서 막대자석의 자기력선은, 오른쪽 그림에서 보듯이, 막대자석의 자기 N극에서 나와서 S극으로 들어가는 방향을 갖는 연속선으로 표시된다. 자기장의 세기는 자기력선의 밀도로 표현된다. 즉 자기력선이 촘촘한 곳은 상대적으로 센 자기장을, 자기장이 성긴 곳은 상대적으로 약한 자기장을 갖는다.
자기장은 보통 크기와 방향을 갖는 벡터 B로 나타내며 자기장의 단위는 국제단위계에서 테슬라(tesla, 기호 T)이다. 자기장 안에서 속도v 로 움직이는 전하 q가 받는 자기력을 로런츠힘이라고 하며 그 크기와 방향은 아래와 같다.
F = q(V ×B).
국제단위계에서 전하 q의 단위는 쿨롱(coulomb, C), 속도 v는 미터 매 초(m/s), 그리고 힘 F의 단위는 뉴턴(newton, N)이므로 B의 단위 테슬라 T는 N·s/(C·m)에 해당한다. 이 식에 의하면 1 T의 자기장은 1 C의 전하를 띠는 입자가 1 m/s의 속도로 그 자기장에 수직 방향으로 입사해 들어갔을 때에 1 N의 힘을 받게 하는 크기임을 알 수 있다.
전류가 흐르는 도선의 주위에 나침반을 가져가면 나침반의 바늘이 도선을 중심으로 동심원을 그리며 정렬하는 것을 관측할 수 있다. 이것은 전류가 흐르는 도선 주위에 동심원 방향의 자기장이 생긴다는 것을 알려준다. 전류가 흐르는 도선 주위에 형성되는 자기장은 비오·사바르의 법칙을 이용하여 구할 수 있다. 그림 2에서처럼, 전류 i가 흐르는 회로에서 원점에 놓인 아주 작은 전류 요소 idI이 r만큼 떨어진 곳에 만드는 자기장 dB(r)을 수식으로 나타내면,
이 된다는 것이 비오·사바르의 법칙이다. 즉, 전류가 흐르는 도선이 만드는 자기장의 크기는 전류의 크기에 비례하고 전류로부터의 거리의 제곱에 반비례하며, 그 방향은 도선을 오른손으로 감쌀 때 네 손가락의 방향이 된다. 여기서 μ₀은 진공의 투자율이고, r^=r/r은 r방향의 단위벡터이다. 이 작은 전류 요소에 의한 자기장을 전체 도선에 대하여 선적분하면 전체 도선에 흐르는 전류에 의한 자기장 B를 구할 수 있다.
한편, 물리학에서는 보통 두 개의 서로 다른 자기장 B와 H를 혼용해서 쓴다. 이 두 자기장은 진공의 투자율(permeability) μ₀와 자기화(magnetization) M을 이용하면
B = μ₀(H + M)
의 관계를 갖는다. 이 두 가지 자기장 가운데 B는 자기유도(magnetic induction) 또는 자기선속밀도(magnetic flux density)라고 부르기도 하며, H는 자기세기(magnetic intensity)라고 부르기도 한다.
역사[편집]
자석과 자기가 훨씬 더 이전에 알려져 있었음에도 자기장에 대한 연구는 1269년 프랑스의 학자 페트루스 페레그리누스(Petrus Peregrinus de Maricourt)가 철 바늘을 이용하여 구 모양의 자석 표면에 자기장을 배치시키면서 시작되었다.
표현[편집]
자기력선[편집]
자기력선(magnetic lines of force)이란 자기장이 뿜어 나오는 모습을 형상화한 일련의 선들이다. 자기장의 방향은 자기력선의 접선의 방향과 같고, 자기장의 세기는 자기력선의 밀도에 비례한다. 자기 홀극이 존재하지 않으므로, 자기력선은 절대로 끊어지지 않는다.
비록 우리가 자기력선을 그릴 때는 화살표 모양으로 그리지만, 그 화살표는 어떠한 실제 운동이나 흐름을 묘사하는 것이 아님을 명심해야 한다. 이는 자기장이 벡터가 아니라는 사실과 관련되어 있다. 엄밀히 말해서 자기장은 벡터가 아니라 유사벡터이다. 이 구분은 대칭성을 이용해 자기장 문제를 분석할 때 중요한데, B가 두 벡터의 벡터곱과 관련되어 있다는 사실(로런츠 힘)로부터 알 수 있다.
극에 대한 오해[편집]
나침반에 써있는 N극과 S극은 지구 자기장의 N극과 S극을 가리키는 것이 아니라 그 반대를 가리킨다.
나침반에 써있는 N극은 지구의 N극이 아니라 북쪽(North)을 가리키게 설계되어 있다. 즉, 자석의 "N극"은 엄밀히 말해 "북극을 향하는 극(north-seeking pole)"이다. 따라서 지구의 남극은 N극이고 북극은 S극이 된다. 자기력선은 자석의 N극에서 나와 S극으로 들어가므로, 실제 지구의 자기력선은 남극에서 나와 북극으로 들어가게 된다.
이렇게 주어진 극에 대한 약속은 비오-사바르 법칙에 나오는 부호 약속, 전하의 부호 약속 등과 마찬가지로 관습적이다.
자기장의 생성[편집]
점전하가 만드는 자기장[편집]
총 자기장은 각각의 전하가 만드는 자기장의 합으로 계산할 수 있다. 점전하가 만드는 자기장은 다음과 같다.
만약 전하가 일정한 속도로 움직이고 있다면, 비오-사바르 법칙을 통해 이 식을 다음과 같이 전개할 수 있다.
벡터 미적분학으로의 표현[편집]
벡터 미적분학을 사용하면 자기장의 생성과정을 수학적으로 간단하고 아름답게 표현할 수 있다. 진공에서,
- ∇×는 회전 연산자이다.
- ∇∙는 발산 연산자이다.
- μ₀는 진공의 투자율이다.
- J는 전류밀도이다.
- ∂는 편미분 연산자이다.
- Ⲉ₀는 진공의 유전율이다.
- E는 전기장을 의미한다.
- t는 시간이다.
첫 번째 방정식은 앙페르 회로 법칙으로 알려진 법칙을 맥스웰이 수정한 것이다. 이 식의 두 번째 항이 바로 맥스웰이 수정한 부분인데, 정적 계(static system)나 준정적 계(quasi-static system)에서는 0이 되어 앙페르의 회로법칙과 일치하게 된다. 두 번째 방정식은 자기홀극이 존재하지 않음을 수학적으로 나타낸 식이다. 이들은 맥스웰 방정식에 포함되며, 여기서 사용된 표기법은 올리버 헤비사이드가 사용한 것이다.
자기장과 상대성 이론[편집]
맥스웰은 자신의 네 가지 방정식을 통해 전기와 자기를 합치는 데 많은 공헌을 했다. 하지만 맥스웰이 만든 체계에서도 전기와 자기는 각각 독립적인 다른 현상으로 존재한다. 하지만 실제로 전기장과 자기장은 전자기 (2차) 텐서라는 한 대상의 두 가지 모습으로, 알베르트 아인슈타인이 특수 상대성 이론을 사용하여 이를 입증했다. 이 이론에 따르면 한 관성계에 있는 관찰자가 자기력을 느낄 때 다른 관성계에 존재하는 관찰자는 전기력을 느낄 수도 있는 것이다. 따라서, 특수상대성이론을 적용하면 자기력은 운동하는 전하의 전기력에 불과함을 보일 수 있고, (특정 관찰자에 대해 상대적인) 운동과 정전기력에 대한 지식으로부터 자기력의 성질을 예측하는 것도 가능하다.
이것을 증명할 수 있는 쉬운 사고실험으로, 무한하고 평행한 두 개의 동일한 도선을 생각해보자. 두 도선에는 동일한 전하가 흐르고 있고, 이들은 서로에 대해 정지해 있으면서 동시에 관찰자 A에 대해서는 동일한 속도로 운동하고 있다. 여기서 두 도선 근처에서 도선과 동일한 속도로 운동하고 있는 또 다른 관찰자 B를 도입하자. 그리고 B가 도선 사이에 척력으로 작용하는 정전기력과 그에 따른 가속도를 측정했다고 하자. A가 측정할 때는 두 도선이 자신에 대해 일정한 속도로 운동하고 있으므로 길이 수축이 일어나게 되고, 이에 따라 두 도선 사이에 작용하는 가속도가 B가 측정한 가속도에 비해 작게 측정될 것이다. 이 감소한 가속도는 인력으로 보이게 되고, 이 인력은 고전전자기학에서 정전기력을 감소시키고 속도가 증가함에 따라 같이 증가하는 항에 해당한다. 이 가상적 힘의 크기는 고전전자기학에서 말하는 전자기력과 정확히 일치한다.
응용[편집]
자기장을 변화시키면 패러데이 전자기 유도 법칙에 의해 전기장과 전류를 유도할 수 있다. 이 전류는 고정된 자기장 속을 운동하는 도체에서도 유도될 수 있다. 이 현상이 바로 발전기와 전동기의 원리다.
회전 자기장[편집]
회전 자기장은 극성을 갖고 비상대론적인 속력으로 회전하는 자기장을 가리킨다. 회전 자기장 안에 있는 영구자석은 외부장에 대해 자세를 유지하려고 한다. 이 현상이 바로 교류전동기의 핵심 작동원리다. 삼상교류 혹은 더 높은 다상교류를 사용하면 좋은 회전 자기장을 얻을 수 있다. 동기전동기와 유도전동기는 고정자의 회전 자기장을 이용해 회전자를 움직인다.
1882년, 니콜라 테슬라는 처음으로 회전 자기장의 개념을 창안했고, 1885년에는 갈릴레오 페라리스(Galileo Ferraris)에 의해 독립적으로 회전 자기장의 개념이 연구되었다. 1888년, 테슬라는 자신의 작업을 통해 미국특허 381968번을 취득했고 같은 해 페라리스는 자신의 연구업적을 토리노의 왕립아카데미에 논문으로 제출했다.
자기장 균열[편집]
최근 태양 주변의 폭발로 인해 지구를 보호하는 자기장 내에 큰 규모의 균열이 발견됐다. 2008년 여름, 두께가 6400km에 이르는 입자층이 지구 대기 바깥에서 관측됐으며 이는 그간 관측된 자기장 균열 규모 가운데 가장 크다고 버클리대 마릿 오이로셋 교수 등이 밝혔다.
동영상[편집]
참고자료[편집]
같이 보기[편집]

 위키원
위키원