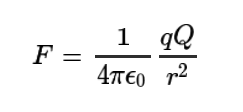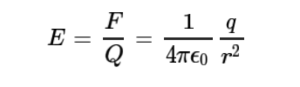"점전하"의 두 판 사이의 차이
(새 문서: '''점전하'''(Point charge)란 부피는 없고, 전하량만 가지고 있는 이론적 존재이다. 수학에서 점과 같은 성질을 가지고 있지만, 전하량은 0...) |
잔글 (→같이 보기) |
||
| (다른 사용자 한 명의 중간 판 3개는 보이지 않습니다) | |||
| 8번째 줄: | 8번째 줄: | ||
[[전하]]는 [[전기장]]에 놓여질 때 힘을 느끼게 하는 물질의 물리적 특성이다. 전하는 서로 상쇄시킬 수 있는 반대되는 특성의 두 가지 종류가 있으며, 이를 양(+)전하와 음(-)전하로 구분하여 표시한다. 같은 극성끼리는 서로 밀어내는 척력이, 다른 극성끼리는 서로 당기는 인력이 작용한다. 많은 경우에 있어서 물질 내에는 양전하와 음전하가 같은 양으로 존재하여 중성을 띠기 때문에 큰 힘이 작용하지 않는다. 전하는 사라지거나 새로 생기지 않으며 총 양이 보존된다. | [[전하]]는 [[전기장]]에 놓여질 때 힘을 느끼게 하는 물질의 물리적 특성이다. 전하는 서로 상쇄시킬 수 있는 반대되는 특성의 두 가지 종류가 있으며, 이를 양(+)전하와 음(-)전하로 구분하여 표시한다. 같은 극성끼리는 서로 밀어내는 척력이, 다른 극성끼리는 서로 당기는 인력이 작용한다. 많은 경우에 있어서 물질 내에는 양전하와 음전하가 같은 양으로 존재하여 중성을 띠기 때문에 큰 힘이 작용하지 않는다. 전하는 사라지거나 새로 생기지 않으며 총 양이 보존된다. | ||
| − | 또한 전하는 양자화되어 있다. 따라서 입자가 띠는 [[전하량]]은 반드시 기본량의 정수배가 된다. 전하량의 국제단위는 [[쿨롱]](Coulomb, 기호)으로, 정전기력에 관한 연구로 유명한 프랑스 물리학자 샤를-오귀스탱 드 쿨롱(Charles-Augustin de Coulomb, 1736~1806)의 이름을 딴 것이다. '''''1C''''은 '''6.25 × 10¹⁸'''개의 양성자들의 전하량이며, 반대로 양성자 한 개의 전하량은 '''1.602177 × 10⁻¹⁹C'''이다. 이러한 양성자 한 개의 전하량을 기본 전하로 부르며, '''''e''''' 또는 '''''q'''''로 표시한다. 전자는 양성자와 크기는 같고 부호는 반대인 전하량을 가진다. 전기나 전자에 대한 지식이 부족했던 시절에 단위를 만들었기 때문에, '''''1C''''은 전하량을 나타내는 단위로써는 굉장히 큰 값을 갖게 되었다. | + | 또한 전하는 양자화되어 있다. 따라서 입자가 띠는 [[전하량]]은 반드시 기본량의 정수배가 된다. 전하량의 국제단위는 [[쿨롱]](Coulomb, 기호)으로, 정전기력에 관한 연구로 유명한 프랑스 물리학자 샤를-오귀스탱 드 쿨롱(Charles-Augustin de Coulomb, 1736~1806)의 이름을 딴 것이다. '''''1C'''''은 '''6.25 × 10¹⁸'''개의 양성자들의 전하량이며, 반대로 양성자 한 개의 전하량은 '''1.602177 × 10⁻¹⁹C'''이다. 이러한 양성자 한 개의 전하량을 기본 전하로 부르며, '''''e''''' 또는 '''''q'''''로 표시한다. 전자는 양성자와 크기는 같고 부호는 반대인 전하량을 가진다. 전기나 전자에 대한 지식이 부족했던 시절에 단위를 만들었기 때문에, '''''1C'''''은 전하량을 나타내는 단위로써는 굉장히 큰 값을 갖게 되었다. |
실제 양성자나 전자는 매우 작지만 부피를 가지고 있으나, 복잡한 상황을 이해하기 위해서는 부피를 무시하고 공간의 한 점에 전하만이 존재하는 이론적 상황으로 단순화하는 것이 효율적이다. 이는 고전역학에서 질량을 가진 입자를 점질량으로 단순화하는 것과 유사하다. | 실제 양성자나 전자는 매우 작지만 부피를 가지고 있으나, 복잡한 상황을 이해하기 위해서는 부피를 무시하고 공간의 한 점에 전하만이 존재하는 이론적 상황으로 단순화하는 것이 효율적이다. 이는 고전역학에서 질량을 가진 입자를 점질량으로 단순화하는 것과 유사하다. | ||
| 17번째 줄: | 17번째 줄: | ||
[[파일:점전하 로부터 거리 인 곳에 있는 시험전하 가 받는 힘.png|썸네일|300픽셀|점전하 로부터 거리 인 곳에 있는 시험전하 가 받는 힘]] | [[파일:점전하 로부터 거리 인 곳에 있는 시험전하 가 받는 힘.png|썸네일|300픽셀|점전하 로부터 거리 인 곳에 있는 시험전하 가 받는 힘]] | ||
[[파일:점전하 로부터 거리 인 곳에서의 전기장과 전기력선.png|썸네일|300픽셀|점전하 로부터 거리 인 곳에서의 전기장과 전기력선]] | [[파일:점전하 로부터 거리 인 곳에서의 전기장과 전기력선.png|썸네일|300픽셀|점전하 로부터 거리 인 곳에서의 전기장과 전기력선]] | ||
| − | 여기서 Ⲉ₀은 진공의 유전율로, '''Ⲉ₀=8.85 × 10⁻¹²''C²/N∙m'''''이다. 경우에 따라서 1/4πⲈ₀ 전체를 상수 '''''k'''''로 표시하기도 하며, 이 때 '''''k = 8.988 × | + | 여기서 Ⲉ₀은 진공의 유전율로, '''Ⲉ₀=8.85 × 10⁻¹²''C²/N∙m'''''이다. 경우에 따라서 1/4πⲈ₀ 전체를 상수 '''''k'''''로 표시하기도 하며, 이 때 '''''k = 8.988 × 10⁹Nm²C⁻²'''''이다. 이러한 힘의 법칙을 쿨롱의 법칙이라 부른다. 즉, 시험전하 '''''Q'''''는 두 전하량의 곱에 비례하고 거리의 제곱에 반비례하는 힘을 받는다. 두 전하의 극성이 같아 힘이 양의 값을 가지면 서로 밀어내는 방향으로, 두 전하의 극성이 달라 힘이 음의 값을 가지면 서로 당기는 방향으로 작용한다. |
| − | [[쿨롱의 법칙]]으로부터, 시험전하 '''''Q | + | [[쿨롱의 법칙]]으로부터, 시험전하 '''''Q'''''가 받는 힘은 시험전하 '''''Q'''''의 전하량의 크기에 비례한다는 것을 알 수 있다. 따라서 점전하 '''''q'''''로 인해 시험전하의 단위전하량 당 받는 힘을 전기장이라 할 수 있다. 즉, 점전하 가 있을 때 이 점전하로부터 거리 만큼 떨어진 곳에서 발생하는 전기장의 크기는 다음과 같다. |
[[파일:전기장 크기.png|썸네일|300픽셀|가운데|]] | [[파일:전기장 크기.png|썸네일|300픽셀|가운데|]] | ||
| 34번째 줄: | 34번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[점]] | ||
* [[전하]] | * [[전하]] | ||
* [[전기장]] | * [[전기장]] | ||
* [[쿨롱의 법칙]] | * [[쿨롱의 법칙]] | ||
| − | + | {{전기|검토 필요}} | |
| − | {{ | ||
2024년 4월 20일 (토) 12:31 기준 최신판
점전하(Point charge)란 부피는 없고, 전하량만 가지고 있는 이론적 존재이다. 수학에서 점과 같은 성질을 가지고 있지만, 전하량은 0이 아니다. 비슷한 개념으로는 물리학에서 사용하는 점질량이 있다. 점질량은 부피는 없고 질량만 가지고 있는 존재이다.
고전전자기학에서 자기장의 정의로서 유한한 크기를 가진 전하 내에서 전기장의 변화가 무시될 때 점전하라 생각할 수 있다. 전기장이란 전기력이 작용하는 공간으로 쿨롱의 법칙에 의해 전하 q가 점전하 +Q로부터 거리 r만큼 떨어진 지점에서 받는 전기장 F는 F=kQq/r²이라 표시된다.
상세[편집]
점전하는 부피가 없이 전하량만 갖고 있으며 공간의 한 점에 존재하는 가상의 이론적 입자이다.
전하는 전기장에 놓여질 때 힘을 느끼게 하는 물질의 물리적 특성이다. 전하는 서로 상쇄시킬 수 있는 반대되는 특성의 두 가지 종류가 있으며, 이를 양(+)전하와 음(-)전하로 구분하여 표시한다. 같은 극성끼리는 서로 밀어내는 척력이, 다른 극성끼리는 서로 당기는 인력이 작용한다. 많은 경우에 있어서 물질 내에는 양전하와 음전하가 같은 양으로 존재하여 중성을 띠기 때문에 큰 힘이 작용하지 않는다. 전하는 사라지거나 새로 생기지 않으며 총 양이 보존된다.
또한 전하는 양자화되어 있다. 따라서 입자가 띠는 전하량은 반드시 기본량의 정수배가 된다. 전하량의 국제단위는 쿨롱(Coulomb, 기호)으로, 정전기력에 관한 연구로 유명한 프랑스 물리학자 샤를-오귀스탱 드 쿨롱(Charles-Augustin de Coulomb, 1736~1806)의 이름을 딴 것이다. 1C은 6.25 × 10¹⁸개의 양성자들의 전하량이며, 반대로 양성자 한 개의 전하량은 1.602177 × 10⁻¹⁹C이다. 이러한 양성자 한 개의 전하량을 기본 전하로 부르며, e 또는 q로 표시한다. 전자는 양성자와 크기는 같고 부호는 반대인 전하량을 가진다. 전기나 전자에 대한 지식이 부족했던 시절에 단위를 만들었기 때문에, 1C은 전하량을 나타내는 단위로써는 굉장히 큰 값을 갖게 되었다.
실제 양성자나 전자는 매우 작지만 부피를 가지고 있으나, 복잡한 상황을 이해하기 위해서는 부피를 무시하고 공간의 한 점에 전하만이 존재하는 이론적 상황으로 단순화하는 것이 효율적이다. 이는 고전역학에서 질량을 가진 입자를 점질량으로 단순화하는 것과 유사하다.
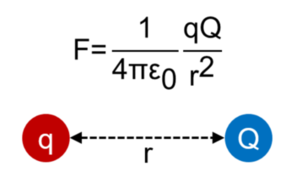
만약 자유공간 상에 점전하 q를 고정하고 거리 r인 곳에 시험전하 Q를 둔다면 이 시험전하 Q가 받는 힘의 크기는 다음과 같다.
여기서 Ⲉ₀은 진공의 유전율로, Ⲉ₀=8.85 × 10⁻¹²C²/N∙m이다. 경우에 따라서 1/4πⲈ₀ 전체를 상수 k로 표시하기도 하며, 이 때 k = 8.988 × 10⁹Nm²C⁻²이다. 이러한 힘의 법칙을 쿨롱의 법칙이라 부른다. 즉, 시험전하 Q는 두 전하량의 곱에 비례하고 거리의 제곱에 반비례하는 힘을 받는다. 두 전하의 극성이 같아 힘이 양의 값을 가지면 서로 밀어내는 방향으로, 두 전하의 극성이 달라 힘이 음의 값을 가지면 서로 당기는 방향으로 작용한다.
쿨롱의 법칙으로부터, 시험전하 Q가 받는 힘은 시험전하 Q의 전하량의 크기에 비례한다는 것을 알 수 있다. 따라서 점전하 q로 인해 시험전하의 단위전하량 당 받는 힘을 전기장이라 할 수 있다. 즉, 점전하 가 있을 때 이 점전하로부터 거리 만큼 떨어진 곳에서 발생하는 전기장의 크기는 다음과 같다.
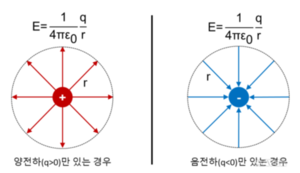
이 전기장의 방향은 양전하인 경우 공간 내 모든 점에서 점전하로부터 바깥쪽으로 뻗어나가는 방향이 되며, 음전하인 경우 공간 내 모든 점에서 바깥쪽으로부터 점전하로 들어오는 방향이 된다. 전기장의 단위는 전하량 당 힘이므로 N/C, 혹은 전위의 개념을 도입하여 V/m이다.
공간의 각 점에서의 전기장을 시각적으로 알아보기 쉽게 나타내기 위하여 전기장을 점전하로부터 뻗어나가거나 들어오는 연속된 곡선의 형태로 나타낼 수 있으며, 이를 전기력선이라고 한다. 만약 양전하만 있다면 전기력선은 전하로부터 출발하여 무한히 먼 바깥으로 뻗어나가고, 음전하만 있다면 무한히 먼 바깥에서 출발하여 전하를 향해 들어오는 형태로 나타난다.
복잡한 전하 분포를 갖는 물체도 0차원의 점전하가 모여진 형태인 1차원의 선전하, 2차원의 면전하, 3차원의 부피전하 등으로 확장함으로써 수식적으로 다룰 수 있게 된다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원