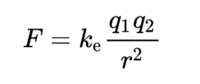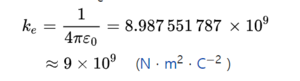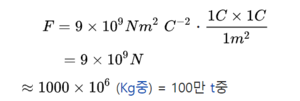"쿨롱의 법칙"의 두 판 사이의 차이
잔글 (→같이 보기) |
|||
| (사용자 2명의 중간 판 2개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''쿨롱의 법칙'''(Coulomb's law)은 두 [[전하 입자]] 사이에 작용하는 정전기적 인력이 두 [[전하]]의 곱에 비례하고, 두 입자 사이의 거리('''''r''''')의 제곱에 반비례한다는 법칙이다. [[역제곱 법칙]]의 | + | '''쿨롱의 법칙'''(Coulomb's law)은 두 [[전하 입자]] 사이에 작용하는 정전기적 인력이 두 [[전하]]의 곱에 비례하고, 두 입자 사이의 거리('''''r''''')의 제곱에 반비례한다는 법칙이다. '''쿨롬의 법칙'''이라고도 한다. 쿨롱의 법칙은 [[역제곱 법칙]]의 하나이다. 이 법칙은 1785년 프랑스의 물리학자이며 토목공학 기술자였던 '''[[샤를 드 쿨롱]]'''(Charles-Augustin de Coulomb)이 비틀림저울을 사용한 실험에서 발견되었다. |
== 개요 == | == 개요 == | ||
| 17번째 줄: | 17번째 줄: | ||
== 비틀림저울을 이용한 실험 == | == 비틀림저울을 이용한 실험 == | ||
| + | [[파일:쿨롱의 비틀림저울 복원품.jpg|썸네일|300픽셀|오른쪽|쿨롱의 비틀림저울 복원품]] | ||
쿨롱은 전하 사이에 작용하는 힘을 정밀하게 측정하기 위해 비틀림 저울을 고안했다. 비틀림 저울에는 움직일 수 없도록 고정된 공과 자유롭게 움직일 수 있는 공의 두 개의 공이 들어 있다. 두 개의 공이 전하를 띠게 되면 자유롭게 움직일 수 있는 공이 회전하게 된다. 이 때 회전하는 방향과 회전하는 정도는 전하의 종류와 전하량에 따라 달라진다. 만약 두 개의 공이 같은 종류의 전하로 대전되면 자유롭게 움직일 수 있는 공은 두 공이 멀어지는 쪽으로 회전하고 다른 종류의 전기로 대전되면 가까워지는 방향으로 회전한다. | 쿨롱은 전하 사이에 작용하는 힘을 정밀하게 측정하기 위해 비틀림 저울을 고안했다. 비틀림 저울에는 움직일 수 없도록 고정된 공과 자유롭게 움직일 수 있는 공의 두 개의 공이 들어 있다. 두 개의 공이 전하를 띠게 되면 자유롭게 움직일 수 있는 공이 회전하게 된다. 이 때 회전하는 방향과 회전하는 정도는 전하의 종류와 전하량에 따라 달라진다. 만약 두 개의 공이 같은 종류의 전하로 대전되면 자유롭게 움직일 수 있는 공은 두 공이 멀어지는 쪽으로 회전하고 다른 종류의 전기로 대전되면 가까워지는 방향으로 회전한다. | ||
| 44번째 줄: | 45번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[쿨롱]] | ||
| + | * [[법칙]] | ||
* [[샤를 드 쿨롱]] | * [[샤를 드 쿨롱]] | ||
* [[전기장]] | * [[전기장]] | ||
| − | |||
* [[전하]] | * [[전하]] | ||
| − | {{ | + | {{전기|검토 필요}} |
2024년 4월 20일 (토) 12:35 기준 최신판
쿨롱의 법칙(Coulomb's law)은 두 전하 입자 사이에 작용하는 정전기적 인력이 두 전하의 곱에 비례하고, 두 입자 사이의 거리(r)의 제곱에 반비례한다는 법칙이다. 쿨롬의 법칙이라고도 한다. 쿨롱의 법칙은 역제곱 법칙의 하나이다. 이 법칙은 1785년 프랑스의 물리학자이며 토목공학 기술자였던 샤를 드 쿨롱(Charles-Augustin de Coulomb)이 비틀림저울을 사용한 실험에서 발견되었다.
개요[편집]
쿨롱의 법칙 – 전기력은 거리 제곱에 반비례하고 전기량의 곱에 비례한다
대부분의 과학책에는 다음과 식으로 나타내진 쿨롱의 법칙이 수록되어 있다.
이 식에서 Q는 전하량을 나타내고 r은 전하 사이의 거리를 나타내면 ke는 쿨롱 상수이다. 두 전하의 부호가 같으면 밀어내고, 다르면 끌어당긴다. 만약 Q1과 Q2가 쿨롱(C)의 단위로 측정한 전기량을 나타내고, r이 전하 사이의 거리를 m단위로 측정한 양이면, 비례상수 k의 크기는 약 90억(좀 더 정확하게는 8.98x10⁹) N·m²/C² 이다.
따라서 1 쿨롱의 전하를 가진 물체가 1 m 떨어져 있을 때 전하 사이에 작용하는 전기력은 약 90억 N(뉴턴)이 된다. 그러나 거리가 10cm로 줄어들면 힘의 크기는 100배가 커져서 9000억 N이 된다.
즉, 각각 1C의 전하량을 갖는 두 점전하가 1m의 거리에 있을 때 발생하는 힘은 1t 트럭 100만 대와 맞먹는다. 이렇게 큰 힘이 기준 단위가 된 것은 전기에 대한 상세한 지식이 없는 시절에 이를 측정 단위로 삼았기 때문이다. 실제 일상 생활에서 발생하는 정전기의 전하량은 대략 ×10⁻⁶에서 ×10⁻⁹ 쿨롱 정도에 불과하다.
비틀림저울을 이용한 실험[편집]
쿨롱은 전하 사이에 작용하는 힘을 정밀하게 측정하기 위해 비틀림 저울을 고안했다. 비틀림 저울에는 움직일 수 없도록 고정된 공과 자유롭게 움직일 수 있는 공의 두 개의 공이 들어 있다. 두 개의 공이 전하를 띠게 되면 자유롭게 움직일 수 있는 공이 회전하게 된다. 이 때 회전하는 방향과 회전하는 정도는 전하의 종류와 전하량에 따라 달라진다. 만약 두 개의 공이 같은 종류의 전하로 대전되면 자유롭게 움직일 수 있는 공은 두 공이 멀어지는 쪽으로 회전하고 다른 종류의 전기로 대전되면 가까워지는 방향으로 회전한다.
쿨롱은 끝에 대전된 공이 달린 막대를 가는 줄에 매달고 줄의 비틀림 탄성을 이용하여 공에 작용하는 전기력을 측정할 수 있었다. 용수철이 가해준 힘에 비례하여 늘어나는 것과 마찬가지로줄도 가해준 토크(힘×거리)에 비례하여 회전하기 때문에 이런 측정이 가능하다. 쿨롱은 공 사이의 거리와 전하량을 변화시켜 가면서 전하 사이에 작용하는 전기력이 어떻게 변화하는 지를 측정하여 전기력이 거리 제곱에 반비례하고 전하량의 곱에 비례한다는 것을 알아냈다. 이런 연구를 통해 쿨롱은 전기력이 뉴턴이 밝혀낸 중력과 마찬가지로 원격작용에 의해 작용하는 힘이라는 개념을 정착시켰다.
쿨롱은 물질에 전기가 흐르는 현상에 대해서도 여러 가지 실험을 했는데 그 중에는 완전한 도체와 완전한 부도체라고 생각되던 물질로 한 실험도 있었다. 그는 실험을 통해 완전한 도체 또는 완전한 부도체는 존재하지 않으며 어떤 한계를 넘으면 부도체에도 전기가 흐른다는 것을 알아냈다.
샤를 드 쿨롱[편집]
쿨롱이 한 연구 중에는 전기와 자기에 관한 연구가 가지 중요하지만 그 밖의 분야에 대해서도 연구를 계속했다. 쿨롱은 1781년부터 1806년 사이에 과학아카데미에 35편의 논문을 제출했다. 그는 이 동안에 보다 진자를 발명한 보다(Jean-Charles, chevalier de Borda, 1733 – 1799), 뛰어난 수학자였던 라플라스(Pierre-Simon, marquis de Laplace, 1749 – 1827) 등과 함께 연구했다. 그는 연구 이외의 활동에도 적극적이어서 과학 아카데미의 310개 위원회의 위원으로 일하기도 했다. 쿨롱은 과학 분야와 관계가 없는 분야에서도 많은 일을 했다. 1784년에는 왕실 분수대를 관리하고 파리에 물 공급을 책임지는 일을 맡았으며, 1787년에는 영국을 방문하고 영국 병원 실태에 대한 보고서를 정부에 제출하여 병원을 개선하는 일도 했다.
1789년 프랑스 대혁명이 일어났을 때 그는 여러 가지 과학과 관련된 프로젝트에 관여하고 있었다. 대혁명으로 많은 연구기관이 재조직되었다. 과학 아카데미는 1793년 8월에 폐쇄되었다가 프랑스 연구소라는 이름으로 다시 문을 열었다. 공직을 떠나 시골에서 혼자 실험하면서 연구를 하고 있던 쿨롱은 프랑스 연구소의 회원으로 선출되자 1795년 12월에 파리로 돌아왔다. 1802년과 1806년 사이에는 프랑스 공립학교의 감찰관으로 임명되어 교육 제도를 개혁하는 일에도 관여했다.
역제곱 법칙[편집]
쿨롱 법칙은 만유인력의 법칙과 같이 역제곱 법칙, 즉 전하를 띤 두 물체 사이에 가해지는 힘이, 거리의 제곱에 반비례한다. 이는 공간이 3차원일 때 일정한 밀도로 퍼져나가는 전기장이 어떤 거리에서 2차원 면을 이루는 것과 관계가 있다.
쿨롱의 법칙이 성립하기 위해 필요한 조건들[편집]
쿨롱의 법칙은 다음과 같은 조건 하에서 성립한다.
- 상호작용하는 전하는 점전하이거나 아니면 유한한 크기의 구대칭 전하밀도 분포를 지녀야 한다.
- 상호작용하는 전하분포는 공간 상에서 서로 겹치지 않아야 한다.
- 상호작용하는 전하는 상대적으로 멈춰 있어야 한다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원