"전기회로"의 두 판 사이의 차이
잔글 (→전기적 법칙) |
잔글 (→같이 보기) |
||
| 44번째 줄: | 44번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[전기]] | ||
| + | * [[회로]] | ||
* [[저항기]] | * [[저항기]] | ||
* [[축전기]] | * [[축전기]] | ||
| 49번째 줄: | 51번째 줄: | ||
* [[전자회로]] | * [[전자회로]] | ||
| − | {{ | + | {{전기|검토 필요}} |
2024년 4월 20일 (토) 12:24 기준 최신판
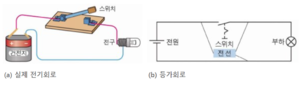
전기회로(Electric Circuit)는 전기가 흐를 수 있도록 설치된 닫힌 회로다. 회로에는 저항기, 축전기, 코일 등 다양한 전기적 소자가 전기 전도체인 전선에 의해 연결된다. 건전지, 전선, 저항을 나란히 이어 만든 폐회로는 가장 간단한 전기회로의 예라고 할 수 있다. 전기회로는 회로에 공급되는 전기의 종류에 따라 크게 직류회로와 교류회로로 나뉘며 각각의 회로에서 저항, 축전기, 코일 등을 연결하여 다양한 전기회로를 만들 수 있다.
전기회로는 전류의 순환회로를 의미하며, 단순히 회로라고도 한다. 전기회로 내 전류의 흐름을 수학적으로 표현하는 두 가지 기본법칙은 옴의 법칙과 키르히호프의 법칙이다.
목차
[숨기기]전기회로의 구성[편집]
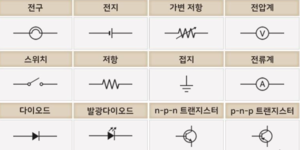
회로는 저항, 콘덴서, 트랜지스터, 진공관 등의 회로소자로 구성되어 있으며, 각 소자는 도선으로 연결된다. 소자는 수동소자와 능동소자로 나눌 수 있다. 수동소자는 에너지를 만들거나 증대시키지 않는 소자로 저항, 콘덴서, 코일 등이 있다. 반면 능동소자는 에너지를 발생, 증대 또는 변환시키는 소자로 트랜지스터, 진공관 등이 있다.
전기회로의 분류[편집]
공급되는 전류의 형태에 따른 분류[편집]
- 직류 회로 : 직류전류가 흐르는 전기 회로
- 교류 회로 : 교류전류가 흐르는 전기 회로
- 삼상 교류
신호에 따른 분류[편집]
전기회로는 회로가 처리하는 신호의 종류에 따라 아날로그 회로와 디지털 회로, 논리회로 등으로 나뉜다.
- 아날로그 회로 : 아날로그 신호를 처리하는 전기 회로로서, 대표적인 예로는 아날로그-디지털 변환회로가 있다.
- 디지털 회로 : 디지털 신호를 처리하는 전기 회로로서, 대표적인 예로는 디지털-아날로그 변환회로가 있다.
- 논리 회로 : 입력 신호를 통해 논리적 연산을 수행하는 회로. 곱연산(And), 합연산(Or), 부정연산(Not)을 수행하는 회로가 있으며 이들을 조합하여 다양한 계산을 할 수 있다.
설계 방법[편집]
어떤 전기 회로도 설계중에 기술자는 회로 일부분의 전압과 전류를 예측할 필요가 있다. 복소수 이론은 단일의 수학적인 표현을 사용하여 모든 선형의 요소를 취급하는 능력을 기술자가 가질 수 있으므로 어느정도의 간단한 선형 회로는 손으로 분석할 수 있다.
그렇지만 대부분의 기술자는 회로 설계시에 시뮬레이션을 하기위해서 특별한 소프트웨어를 사용한다. 모든 회로의 패턴을 테스트할 필요가 없기 때문에 실제로 회로를 구현해서 테스트하는 것 보다더 시간이나 돈이 절약된다. 그리고 VHDL같은 기술의 개발은 시뮬레이션으로 자동으로 회로 설계를 생성하는 것이며 이것은 기술자로부터 많은 부담을 덜어주었다.
전기적 법칙[편집]
아무리 복잡한 전기회로일지라도 회로는 기본적으로 전자기 법칙을 따르게 된다. 따라서 전자기 법칙으로부터 도출된 여러 가지 정리를 통해 복잡한 전기회로에 대한 분석 및 설계가 가능하다. 선형으로 설계된 전기회로에서 적용가능한 유용한 전기적 법칙 중 대표적인 것으로는 키르히호프의 법칙, 옴의 법칙, Y-Δ 변환공식, 테브난의 정리, 제뉴어리의 정리, 밀돈의 정리 등이 있다.
- 키르히호프의 법칙 (전류법칙) : 전기 회로의 임의의 지점에서 유입하는 전류와 유출하는 전류의 합은 같다.
- 키르히호프의 법칙 (전압법칙) : 전기 회로의 임의의 폐회로에서 전압의 방향을 한방향으로 계산하면 전압의 총합은 0이 된다.
- 옴의 법칙 : 어떤 저항에 걸린 전압은 저항값과 전류에 비례한다.
- Y-Δ 변환 : 전기회로를 간략하게 만들기 위한 것으로 Y모양의 회로와 Δ모양의 회로 사이의 변환공식.
- 테브난의 정리 : 선형 연결된 임의의 전기회로에 대해 하나의 전압, 하나의 저항(단일 주파수의 교류회로의 경우는 임피던스)의 직렬연결로 구성되는 동등한 회로가 존재한다.
- 노튼의 정리 : 선형 연결된 임의의 전기회로에 대해 하나의 전압, 하나의 저항(단일 주파수의 교류회로의 경우는 임피던스)의 병렬연결로 구성되는 동등한 회로가 존재한다.
- 밀먼의 정리 : 병렬로 연결된 회로를 간단히 하는 공식으로, 러시아의 전기공학자 야콥 밀먼(Jacob Millman)이 증명한 정리.
회로가 비선형이거나 리액턴스가 포함된 경우에는 보다 복잡한 법칙이 필요하다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원