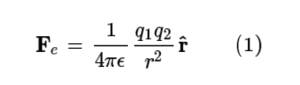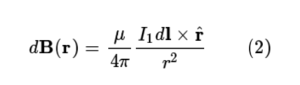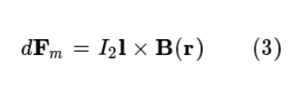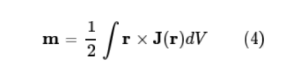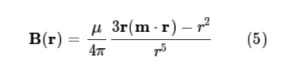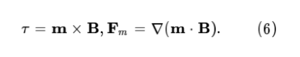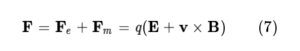"전자기력"의 두 판 사이의 차이
잔글 (→전기력) |
잔글 (→같이 보기) |
||
| 57번째 줄: | 57번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[전기]] | ||
| + | * [[자기 (물리)]] | ||
| + | * [[전자기]] | ||
* [[전기력]] | * [[전기력]] | ||
* [[자기력]] | * [[자기력]] | ||
| 63번째 줄: | 66번째 줄: | ||
* [[로런츠힘]] | * [[로런츠힘]] | ||
| − | {{ | + | {{전기|검토 필요}} |
2024년 4월 20일 (토) 12:27 기준 최신판
전자기력(Electromagnetic force)은 4대 기본 힘 중 하나로, 전기력과 자기력을 통칭하는 용어이다. 게이지 보손인 광자가 매개하는 힘. 전자기 상호작용이라고도 한다. 이전에 분리되어 있던 전기력과 자기력을 제임스 클러크 맥스웰이 통합시켜 정립된 힘이다.
개요[편집]
물질의 근원적 기본 상호작용에는 네 가지 종류가 있다. 이 네 가지는, 만유인력 또는 중력으로 일컫는 질량을 가진 입자들 사이의 상호작용, 전자기력 또는 전자기상호작용으로 일컫는 원자핵보다 먼 거리의 전하를 띤 입자들 사이의 상호작용, 그리고 강력 또는 강한 상호작용으로 일컫는 원자핵 내부의 상호작용, 약력 또는 약한 상호작용으로 일컫는 원자핵 내부에서 붕괴 방출 작용과 관련된 상호작용이다. 이 중 전자기력은 물체의 무게를 제외하면, 일상 생활에서 접할 수 있는 거의 모든 힘의 근원이 된다고 할 수 있다.
전자기력을 매개하는 보손은 광자이며, 전하나 자기모멘트를 가진 모든 개체 사이에 작용할 수 있는 힘이다. 전통적으로 전기력과 자기력을 구분하여 왔으나, 근본적으로 같은 힘인 사실이 맥스웰 이론과 전자기파, 그리고 특수상대성이론에 의하여 밝혀졌다. 양자전기역학의 근간이 된다. 전자기장의 크기가 밝혀지면, 전하가 받는 전자기력은 로런츠힘으로 결정된다.
전기력[편집]
전기력은 전하를 띤 두 물체 사이에 작용하는 힘이다. 쿨롱의 법칙에 의하면, 전하를 띤 두 점전하(point charge) 사이에는 다음의 전기력 Fe가 작용한다.
여기서 Ⲉ는 공간의 유전율, q1, q2는 각 입자의 전하량을 표시하고 r은 두 점전하 사이의 거리이며, hatr은 거리 방향의 벡터를 의미한다. 두 전하량의 부호가 같으면 Fe는 길이가 늘어나는 방향으로 작용하여 서로를 밀쳐내는 척력이 되며, 두 전하량의 부호가 서로 다르면 Fe는 길이가 줄어드는 방향으로 작용하여 서로를 당기는 인력이 된다. 진공에서의 1/4πⲈ값은 약 9 ×10⁹ Nm²C⁻²이어서, 1 C의 두 점전하가 1 m 떨어져 있을 때의 힘의 크기는 9 ×10⁹이 된다.
전기장 E는 1 C의 단위 전하량을 갖는 시험 전하(test charge)가 받는 힘으로 이해할 수 있다. 하나의 전하 q1이 전기장을 만들면 다른 전하 q2는 그 전기장에 의해 전기력을 받는 것으로 생각할 수 있다. 반대로 작용 반작용 법칙에 의하여 q2이 만든 전기장에 의해 q1도 힘을 받는다. 전하량 q에 대해 F = qE의 관계가 있다.
자기력[편집]
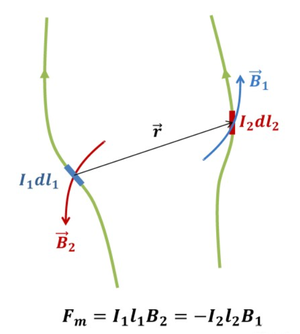
자기력은 전류나 자기모멘트 사이에 작용하는 힘이다. 전류나 자기모멘트는 주위에 자기력이 미치는 공간인 자기장을 만든다. 그리고 그 자기장 하에 놓인 다른 전류나 자기모멘트는 자기장에 의한 자기력을 받는다. 전류와 전류 사이에 작용하는 자기력은 다음과 같이 나타낼 수 있다.
자기장을 만드는 전류를 I₁, 그리고 자기장에 의한 자기력을 받는 전류를 I₂ 라 하자. 비오·사바르의 법칙에 의하면, 그림 1과 같이 원점에 놓인 전류 요소 I₁dI이 r만큼 떨어진 곳에 형성하는 자기장 dB는 다음과 같이 나타난다.
여기서 μ는 투자율이고, r^은 전류 요소와 r지점 사이의 변위 방향의 단위벡터이다. 전체 도선에 의한 자기장은, 이 전류 요소에 의한 기여를 도선에 대해 적분하여 얻을 수 있다. 무한히 긴 직선의 도선의 경우를 가정하면, B(r) = μI₁/2πd ∙ ∅^가 되는데, 이때 d는 도선으로부터 관측 지점의 거리, ∅^는 도선을 시계 반대 방향으로 감싸는 방향의 원주 방향 단위벡터이다.
위의 계산을 통해 얻은 자기장 B(r)에 의하여, 전류 요소 I₂dI이 받는 자기력 요소 dFm은 다음과 같이 주어진다.
I₁ 과 I₂ 가 평행하고 거리 d만큼 떨어져 있는 경우, I₂에 작용하는 자기력을 적분하여 얻으면, Fm = -I₂lBd^ = -μI₁I₂l/2πd ∙ d^가 된다. 작용 반작용 법칙에 의하여 I₁에 작용하는 자기력을 적분하여 Fm을 구하면 크기는 같고 부호는 반대가 된다. d^는 두 도선 사이 거리가 늘어나는 방향이므로, I₁과 I₂의 전류 방향이 같은 방향이면 인력이, 반대 방향이면 척력이 작용한다는 사실을 알 수 있다.
전류가 아닌 자기모멘트가 만드는 자기장은 자기쌍극자에 의한 자기장으로 나타난다. 전류밀도 J(r)에 의한 자기모멘트 m은 식 4와 같이 부피 적분으로 주어진다.
그리고 자기모멘트에 의한 자기쌍극자의 자기장은 다음 식 5와 같다.
주어진 자기장 B에 의하여 자기모멘트는 돌림힘 r와 자기력을 받으며 각각 다음과 같이 표현할 수 있다.
로런츠힘[편집]
미시적 관점에서 보면, 전류는 전하의 운동이므로, 전하 하나의 속도가 v일 때 받는 전기력과 자기력을 생각할 수 있다. 이를 로런츠힘이라 한다. 로런츠힘은 전기장 또는 자기장 하에서 움직이는 전하가 받는 힘이다. 전하의 전하량을 q, 속도를 v라 하면, 로런츠힘은 식 7과 같이 주어진다.
즉, 양의 전하를 띤 입자는 전기장 방향으로 그리고 속도와 자기장에 수직인 방향으로 힘을 받게 된다.
로런츠힘의 방향에 대해 쉽게 생각하기 위해 흔히 플레밍의 왼손법칙을 이용한다. 왼손법칙은, 그림 3에서처럼, 자기장 B와 전류 I의 방향이 서로 수직일 때 도선이 받는 힘 F의 방향을 왼손의 엄지(F)와 검지(B), 중지(I)를 이용하는 것이다. 식 4는 외적(cross product)으로 표현되므로, v와 B에서 서로 수직인 성분만 로런츠힘을 제공한다. 따라서 B에 평행한 v 성분은 고려할 필요가 없으며, 자기장에 평행한 전류나 움직이는 전하는 로런츠힘을 받지 않는다. 전자의 경우에는 음전하이므로, I 의 방향은 전자 진행 방향의 반대 즉, -v방향임에 주의하여야 한다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원