기술진보
기술진보(技術進步, technical progress)는 생산 요소의 축적과 더불어 경제성장의 요인으로 생산 요소의 투입을 감소시켜 기존과 동일한 생산 수준을 얻거나 상품의 질을 향상시키는 생산성의 증가이다.
개요
기술진보는 생산기술에 관한 새로운 방법의 이용 또는 새로운 생산함수(生産函數)의 도입을 의미하는 말이다.
좁은 뜻의 기술혁신과 같은 뜻이다. 경제발전 또는 경제성장에 대한 기술진보의 중요성에 대한 인식이 높아지고, 그와 함께 기술진보에 관한 이론적 및 실증적(實證的) 연구가 많이 발표되고 있다. 생산함수 안에서 기술진보는 다음과 같이 다룬다. 산출량(産出量) Y가 자본재(資本財) K(Y와 같은 財라고 한다)와 노동력L에 의하여 생산되는 것이라고 하고, 또한 각 시점에서의 기술목록표(技術目錄表)를 T로 나타내면 생산함수는 일반적으로 Y=F(K, L, T) 라고 나타낼 수 있다. 기술진보란 기술목록표T의 향상에 따른 산출량 Y의 증대를 뜻한다. 만일, 기술진보 효과를 구체화하기 위해 자본재의 새로운 건설은 필요하지 않다고 하면(이것을 구체화되지 않는 기술진보라 한다), 단위시간에서의 기술진보율(技術進步率)은 간단하게
(∂Y/∂T ·dT/dt)/Y
라고 나타낼 수 있을 것이다. 여기서 t는 시간이다.
미국의 경제학자 R.M.솔로는 1909년부터 49년까지 미국의 비농업 민간부문에 있어서의 기술진보율이 전반기에는 약 1%, 후반기에는 약 2%임을 계측하였다. 기술진보에 대해서는 전통적으로 소득분배율에 미치는 효과가 문제되어 왔다. 그리고 적당한 규준 아래에서 소득분배율을 변함없이 유지하는 기술진보는 중립적이라고 한다. 요소에 대한 보수율(報酬率)이 한계생산력(限界生産力)과 같다는 전제 아래에서, 생산함수가 Y = T ·F (K,L) 이라는 형식으로 나타나면 J.R.힉스가 주장하는 뜻에서 중립적이며, 생산함수가 Y =F ( K, T ·L ) 이라는 형식으로 나타나면 R.F.하로드가 주장하는 뜻에서 중립적이며, 그리고 생산함수가 Y =F (T·K,L) 이라는 형식으로 나타나면 솔로가 주장하는 뜻에서 중립적이라고 할 수 있다. 이상에서는 자본재에 의하여 구체화되지 않는 기술진보를 문제로 삼았으나, 기술진보를 구체화하기 위해서는 새로운 자본재가 필요하다는 견해가 나오고 있다. 이런 주장에 입각하여 경제성장론을 해석하는 일이 오늘날 이론경제학의 중요한 과제의 하나이다.
- 중립적 기술 진보(中立的技術進步 ): 경제 영국의 경제학자 힉스가 정의한 기술 진보의 한 유형. 주어진 노동ㆍ자본 비율에 대하여 노동의 한계 생산과 자본의 한계 생산의 비율이 변하지 않고 생산 기술의 특징이 유지되는 기술 진보를 말한다.
- 힉스 중립적 기술 진보(Hicks中立的技術進步) : 경제 영국의 경제학자 힉스가 정의한 기술 진보의 한 유형. 주어진 노동ㆍ자본 비율에 대하여 노동의 한계 생산과 자본의 한계 생산의 비율이 변하지 않고 생산 기술의 특징이 유지되는 기술 진보를 말한다.
- 자본 절약적 기술 진보(資本節約的技術進步) : 경제 노동에 비하여 자본을 더 적게 사용하고도 더 많은 산출량을 생산하게 하는 기술의 발전을 말한다.
- 노동 절약적 기술 진보(勞動節約的技術進步) : 경제 자본에 비하여 노동력을 더 적게 사용하여 제품을 더 많이 생산하는 기술의 발전을 말한다.
상세
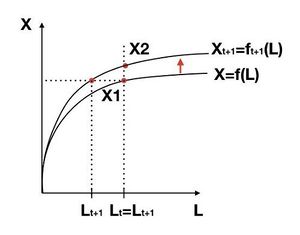
기술 진보는 사실 거시경제학에서 더 중요한 개념이다. 쉽게 말해서 기술력이 좋아져서 생산성이 높아지는 건데 이전에는 노동력(L) 10을 투입해야 빵(X)을 8개를 생산할 수 있었는데 이제는 노동력을 8만 투입해도 빵 8개를 생산 할 수 있게 된 것이다. 그러면 전체적으로 생산함수가 상방으로 이동하게 된다. 그러면 만약에 기술 진보 후에도 여전히 빵 8개를 생산한다고 가정할때는 Lt - Lt+1 만큼 노동력을 절감하는 것이고, 노동력을 10을 그대로 투입한다고 할때는 X2-X1만큼 생산력이 증가하는 것이다.
- 기회비용 (Opportunity cost)
그 다음엔 기회비용이라는 개념이 나오는데 내가 무언가 한가지를 하기 위해서는 다른 한가지를 포기해야 한다. 동시에 할 수 있는 것이 없다. 예를 들자면 내가 지금 이 시간에 공부를 할 것인가 아니면 여자친구와 데이트를 해야할 것인가 둘 중에 하나를 선택해야 한다. 공부를 한다면 나의 성적이 향상될 것이고 데이트를 한다면 여자친구와의 관계가 개선될 것이다. 하지만 둘 중에 하나를 선택해야한. 여자친구와 관계가 좋을 때는 내가 차일 염려가 없기 때문에 공부를 하는게 더 효율적이라고 생각하겠지만 여자친구와 위태위태하다라고 하면 공부하는 것보다 여자친구와 관계개선이 더 효율적이다.
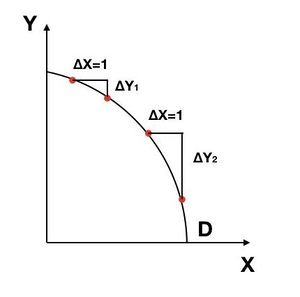
여기 이 세상에 다시 X와 Y라는 생산품만 있다. 나에게 주어진 노동력에 따라 X,Y생산품 갯수가 달라지는데 X 1개를 추가로 생산하려면 Y 몇 개를 포기해야 하는지 보여주는 것이다. 문제는 이 생산가능 곡선이 '곡선'이라는 것이다.
생산함수에서 보셨 듯이 노동력을 처음 투입하기 시작할 때는 생산성이 확 올라가는데 어느 지점부터는 노동력 두 배를 투입해도 생산력이 두배로 오르지 않고 조금밖에 오르지 못한다. 마치 내가 시험기간에 2시간을 공부하면 C를 받을 수 있지만 최소 15시간을 공부해야 A를 받을 수 있는 것처럼 말이다.
그런 생산함수의 특성때문에 생산가능곡선도 이렇게 '곡선'으로 나오는데 그래서 각각의 지점에 따라 내가 Y생산품을 몇개 포기해야하는지도 다르다. 그것을 '기회비용'이라고 한다.
- 파레토 효율 (Pareto efficiency)
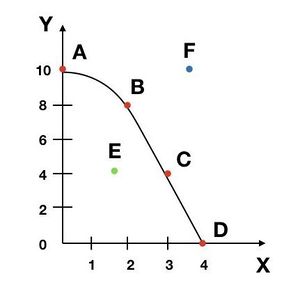
똑같은 그래프가 한번 더 나왔다. 파레토 효율이라는 개념을 설명하기 위해서이다. 개념은 간단하다. 예를 들어 한정된 자원에서 Y를 한 개 더 생산하려고 할 때 X를 포기하지 않고서는 Y를 하나 더 생산하지 못하는 상태를 파레토 효율이라고 한다. 이 그래프에서 F는 중요하지 않다.
E를 보면 E 지점에서는 X나 Y 생산을 포기하지 않고도 전체 생산량을 늘릴 수 있다. 그러므로 파레토 효율이 아니다. 하지만 B,C,D 지점 모두 다 X의 생산을 포기하지 않고서는 Y를 더 생산할 수 없다. A도 마찬가지로 Y의 생산을 포기하지 않고서는 X를 생산할 수 없다. X든 Y든 상관이 없다.
결론은 생산가능곡선의 곡선상에 있는 상태만 파레토 효율이라고 볼 수 있고 곡선 안쪽은 파레토 효율이 아닌 상태이고 곡선 바깥쪽은 불가능의 영역이라고 보면 된다.
참고자료
- 〈기술진보〉, 《네이버 국어사전》
- 〈기술진보〉, 《두산백과》
- 직대딩, 〈단기생산함수, 장기생산함수와 기술진보〉, 《티스토리》, 2018-04-19
- 물티쿨티(multikulti) , 〈기술진보, 기회비용, 파레토 효율〉, 《티스토리》, 2018-05-10
같이 보기

 위키원
위키원