해시넷
"4D"의 두 판 사이의 차이
| 14번째 줄: | 14번째 줄: | ||
=== 4차원 공간 === | === 4차원 공간 === | ||
| − | 수직선 4개가 직교하는 공간이라는 것은 좌표축이 4개 있다는 것과 같다. 즉, 4차원은 한 점에 한 점에 막대 4개를 모두 서로 직교하게 놓을 수 있어야 한다. 하지만 우리가 사는 세상은 3차원이므로 이는 불가능한 일이다. 4개의 좌표축을 그릴 수 있는 방법은 다음과 같다. 만약 종이 안의 구면 좌표계에 사람 알파가 살고 있다고 가정하면 그 사람은 좌표축 3개가 직교된 모습을 그릴 수 있다. 하지만 그려진 3개의 좌표측에 모두 수직인 직선은 어떻게 해도 그릴 수 없다. 이때 종이 밖에 있는 현실의 사람인 베타가 막대를 가져와 종이에 그려진 좌표의 원점에 수직으로 세운다. 그럼 베타의 입장에서는 종이 안에서 직교하고 있는 3개의 좌표축 모두와 수직인 직선을 세운 셈이다. 이때 종이 위에 세운 막대가 바로 네 번째 좌표축이 되고 알파에게 베타가 있는 공간은 4차원이다. 해당 개념을 적용해 우리는 우주를 4차원이라고 한다. 하지만 이와 같이 현실에서 말하는 4차원은 사실 3차원 공간에 1차원 시간을 더한 '4차원 시공간'이며 4차원 공간이 아니다. | + | 수직선 4개가 직교하는 공간이라는 것은 좌표축이 4개 있다는 것과 같다. 즉, 4차원은 한 점에 한 점에 막대 4개를 모두 서로 직교하게 놓을 수 있어야 한다. 하지만 우리가 사는 세상은 3차원이므로 이는 불가능한 일이다. 4개의 좌표축을 그릴 수 있는 방법은 다음과 같다. 만약 종이 안의 구면 좌표계에 사람 알파가 살고 있다고 가정하면 그 사람은 좌표축 3개가 직교된 모습을 그릴 수 있다. 하지만 그려진 3개의 좌표측에 모두 수직인 직선은 어떻게 해도 그릴 수 없다. 이때 종이 밖에 있는 현실의 사람인 베타가 막대를 가져와 종이에 그려진 좌표의 원점에 수직으로 세운다. 그럼 베타의 입장에서는 종이 안에서 직교하고 있는 3개의 좌표축 모두와 수직인 직선을 세운 셈이다. 이때 종이 위에 세운 막대가 바로 네 번째 좌표축이 되고 알파에게 베타가 있는 공간은 4차원이다. 해당 개념을 적용해 우리는 우주를 4차원이라고 한다. 하지만 이와 같이 현실에서 말하는 4차원은 사실 3차원 공간에 1차원 시간을 더한 물리학 단어인 '4차원 시공간'이며 4차원 공간이 아니다. |
4차원 공간의 모습을 상상하기 힘든 이유는 바로 우리가 3차원 공간에서 살고 있으며, 4차원 공간을 직접 본 적이 없기 때문이다. 또한 일상 생활에서 4차원을 그려야 할 일도 없어 4차원 공간의 모습이 쉽게 떠오르는 것이 오히려 신기한 일이다. 따라서 4차원 도형을 구현한 영상을 보아도 3차원 물체가 연결된 채로 원운동과 자유변형까지 하는것을 알아보는것은 매우 힘든일이다.<ref name = '4D나무'/> | 4차원 공간의 모습을 상상하기 힘든 이유는 바로 우리가 3차원 공간에서 살고 있으며, 4차원 공간을 직접 본 적이 없기 때문이다. 또한 일상 생활에서 4차원을 그려야 할 일도 없어 4차원 공간의 모습이 쉽게 떠오르는 것이 오히려 신기한 일이다. 따라서 4차원 도형을 구현한 영상을 보아도 3차원 물체가 연결된 채로 원운동과 자유변형까지 하는것을 알아보는것은 매우 힘든일이다.<ref name = '4D나무'/> | ||
| 57번째 줄: | 57번째 줄: | ||
* 균일 4차원 다포체 : 아르키메데스 다면체의 4차원 버전이다. | * 균일 4차원 다포체 : 아르키메데스 다면체의 4차원 버전이다. | ||
* 쌍곡포물입체, 타구포물입체, 타구입체 등<ref name = '4D나무'/> | * 쌍곡포물입체, 타구포물입체, 타구입체 등<ref name = '4D나무'/> | ||
| + | |||
| + | === 4차원 도형 재현 === | ||
| + | 3차원을 2차원에 완벽히 표현할 수 없으나 3차원의 그림자를 2차원에 투영할 수 있는 것과 같이, 시각적으로 재현한 4차원 도형들은 사실 3차원에 투영된 실제 4차원 도형의 그림자를 구현한 이다. 3차원 공간에 살고 있는 우리는 4차원 도형을 상상하기 힘들며 표현하기는 불가능하기 때문이다. 우리가 알고 있는 4차원 도형들은 실제 모습이 아닌, 모두 3차원 공간의 인간의 상상으로 만들어낸 가상의 도형들이다.<ref name = '4D나무'/> 3차원의 정육면체의 각 면은 정사각형으로 이루어져 있으나 2차원의 평면에 그려내면서 실제모습과는 다르게 앞면과 뒷면을 제외하고는 평행사변형으로 표현되는 등 왜곡이 일어난다. 2차원 평면에 3차원을 그리려면 한차원만 확장하면 되기 때문에 약간의 왜곡만이 일어나지만 4차원을 2차원에 그려내는 일은 두개의 차원을 확장하는 것 이기 때문에 더욱 심한 왜곡과 한계가 생긴다.<ref name='4차원 입체도형'/> | ||
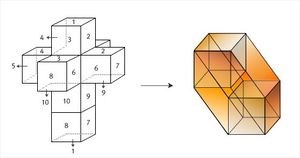
| + | [[파일:초입방체.jpg|오른쪽|초입방체 전개도|300픽셀]]이러한 상상의 도형을 만들거나 연구하는데는 스케치업이나 쓰리디에스 맥스[3ds max] 같은 3차원프로그램이 어느정도 도움을 준다. 3차원을 2차원 종이에 그림으로 그려 표현하듯 4차원을 3D프로그램에 그려 나타내는 것 이다. 하지만 프로그램을 이용해도 사실 4차원을 3차원 프로그램을 나타내는것을 2차원인 평면 모니터를 통해 보는 것 이기 때문에 그리거나 이해하는데 공간지각능력이 3차원을 넘어 4차원까지 다룰 수 있는 초월적 지각 능력을 가져야 한다. x,y,z 세 가지 축에 하나의 축 a를 추가로 가진 포디 그래퍼(4D Grapher)과 같은 4차원 프로그램이 존재하긴 하지만 사실 4차원의 그림을 그린다기 보다는 4차원 그래프를 분석하기 위한 용도에 더 적합하다.<ref name = '4D나무'/> | ||
| + | 4차원의 도형을 보다 정확하게 재현하는 방법은 바로 전개도를 이용하는 것이다. 정육면체를 전개해서 2차원 면으로 구성된 전개도를 만들고 다시 1차원인 선끼리 붙여 정육면체를 만드는 방법과 같이 4차원 초입방체에서 접힌 부분을 펴내면 모든 각이 직각을 이룬 8개의 정육면체가 맞붙은 십자가 모양의 전개도가 나온다. 이 전개도를 다시 2차원면끼리 맞붙이면 4차원 초입방체가 된다.<ref name='4차원 입체도형'/> | ||
=== 테서랙트 === | === 테서랙트 === | ||
[[파일:테서랙트.gif]] | [[파일:테서랙트.gif]] | ||
| − | 테서렉트는 영국 출신의 수학자 찰스 하워드 힌턴(Charles Howard Hinton)이 | + | 테서렉트는 영국 출신의 수학자 찰스 하워드 힌턴(Charles Howard Hinton)이 1888년 4차원물체의 시각화를 돕기 위해 고안한 개념으로, 듀오 프리즘의 한 종류이며 4차원 초입방체 또는 정팔포체 라고도 한다. 3차원 도형인 정육각형의 전개도를 만들면 2차원의 정사각형으로 구성되어있는것 처럼, 4차원인 테서랙트를 전개도로 만들면 3차원인 정육각형으로 구성되었다. 인간의 감각기관은 4차원 이상을 인지 할 수 없기 때문에 테서랙트를 3차원 공간에 투영된 형태로 인지한다.<ref name='테서랙트'> 〈[https://namu.wiki/w/%ED%85%8C%EC%84%9C%EB%9E%99%ED%8A%B8 테서랙트]〉, 《나무위키》</ref> 따라서 관련 테서랙트의 모습을 보면 실제 모양을 보면 상상하기 힘들지만, 4차원 공간상에서의 테서랙트는 모든 정육면체가 서로 수직이고 각 정육면체의 평면도 직각을 이룬다. 위 자료의 테서랙트는 4차원 공간 축을 따라 회전하는 테서랙트이다. 3차원 물체 2개가 연결된 채 원운동과 자유변형까지 동시에 하기 때문에 알아보기 힘들지만, 사실 테서랙트의 회전 중에서는 비교적 단순한 형태의 움직임을 구현한것 이다.<ref name='4차원 입체도형'/> 한편 테서랙트를 여러 개 활용하면 더 고차원의 도형을 만들 수 있다. 테서랙트10개를 한 모서리당 3개씩 만나도록 연결하면 5차원 도형인 펜터랙트(Penteract)가 만들어진다.<ref name='테서랙트'/> |
| − | + | 테서랙트가 미지의 영역에 대한 신비로움을 담은 4차원의 상징이 되면서, 테서랙트라는 개념이 발표 된 후 과학뿐만 아니라 여러 인문철학, 예술 등에도 많은 영향을 미쳤다. | |
| − | + | * 스페인의 초현실주의 화가인 살바도르 달리(Salvador Dalí)는 이 초입방체의 전개도를 자신의 작품에 그려넣기도 했다. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== 물리학 관점 == | == 물리학 관점 == | ||
| − | == 영화 == | + | == 예술 == |
| − | === 인터스텔라 === | + | === 영화 === |
| + | ==== 인터스텔라 ==== | ||
| − | === 영화관 === | + | ==== 영화관 ==== |
==== 씨지브이(CGV) ==== | ==== 씨지브이(CGV) ==== | ||
| 84번째 줄: | 85번째 줄: | ||
==== 엠엑스포디(MX4D) ==== | ==== 엠엑스포디(MX4D) ==== | ||
| − | == | + | === 그림 === |
https://terms.naver.com/entry.naver?docId=3568440&cid=58944&categoryId=58970 | https://terms.naver.com/entry.naver?docId=3568440&cid=58944&categoryId=58970 | ||
| − | + | https://blog.naver.com/ian3714/220293166087 | |
| + | 스페인의 초현실주의 화가인 살바도르 달리(Salvador Dalí)는 이 초입방체의 전개도를 자신의 작품에 그려넣기도 했다 | ||
{{각주}} | {{각주}} | ||
2021년 7월 14일 (수) 12:00 판
4D(포디, Fourth Dimension)란 4개의 차원으로 이루어진 임의의 공간으로, 4차원 이라고도 한다. 수식어로서 3차원에 사는 일반인은 이해할 수 없는 무엇이라는 뜻을 가지기도 한다.[1]
목차
4차원의 이해
공간
공간의 사전적 정의는 어떤 물질 또는 물체가 존재할 수 있거나 어떤 일이 일어날 수 있는 장소이다.[2] 공간은 거리와 길이, 각도를 반영한 좌표계를 도입하여 임의 차원의 공간으로 확장한[3] 수학에서의 유클리드 공간을 비롯해 관점에 따라 다양하게 존재한다. 주로 물리학, 천문학, 수학, 불교, 철학등으로 나뉘며, 같은 분야에서도 공간에 대한 정의는 여러 의미와 종류로 나뉠 수 있다.[2] 이때 4차원에서 말하는 공간은 물리학적 공간에서는 존재할 수 없다.[4]
차원
어떠한 공간에 대해 차원이라고 하는 것은 그 공간의 성분 중 서로에게 영향을 미치지 않고 독립적으로 움직일 수 있는 성분들의 최대 개수이다. 즉 서로 영향을 끼치지 않는 4가지 성분을 나타낼 수 있으면 그것은 4차원이다.
성분을 데이터로 하여 예로 들어 생각해보면 어떤 사람 에이(A)에 대한 수치 데이터를 다룬다고 가정한다. 이때 이 사람의 키, 몸무게, 가족수, 재산을 통계로 만들면 에이(A)라는 사람은 (172cm, 64kg, 4명, 5억 원)이라는 4개의 숫자쌍으로 정의할 수 있다. 이때 각각의 정보는 서로 영향을 주지 않는 독립된 정보이다. 따라서 위와 같이 나타낸 순서쌍은 4차원 데이터 라고 할 수 있다.[5]
기하학적으로 예를 들면 우리가 사는 3차원은 3개의 직선이 앞뒤, 좌우, 위아래의 3가지 방향으로 자유롭게 움직일 수 있는 공간을 뜻하며, 마찬가지로 적용하면 4차원은 수직선 4개가 서로 직교하는 공간인 것이다. 이때 4차원은 평면에 그릴 수 없고 머릿속으로 상상만 할 수 있다.[6]
4차원 공간
수직선 4개가 직교하는 공간이라는 것은 좌표축이 4개 있다는 것과 같다. 즉, 4차원은 한 점에 한 점에 막대 4개를 모두 서로 직교하게 놓을 수 있어야 한다. 하지만 우리가 사는 세상은 3차원이므로 이는 불가능한 일이다. 4개의 좌표축을 그릴 수 있는 방법은 다음과 같다. 만약 종이 안의 구면 좌표계에 사람 알파가 살고 있다고 가정하면 그 사람은 좌표축 3개가 직교된 모습을 그릴 수 있다. 하지만 그려진 3개의 좌표측에 모두 수직인 직선은 어떻게 해도 그릴 수 없다. 이때 종이 밖에 있는 현실의 사람인 베타가 막대를 가져와 종이에 그려진 좌표의 원점에 수직으로 세운다. 그럼 베타의 입장에서는 종이 안에서 직교하고 있는 3개의 좌표축 모두와 수직인 직선을 세운 셈이다. 이때 종이 위에 세운 막대가 바로 네 번째 좌표축이 되고 알파에게 베타가 있는 공간은 4차원이다. 해당 개념을 적용해 우리는 우주를 4차원이라고 한다. 하지만 이와 같이 현실에서 말하는 4차원은 사실 3차원 공간에 1차원 시간을 더한 물리학 단어인 '4차원 시공간'이며 4차원 공간이 아니다.
4차원 공간의 모습을 상상하기 힘든 이유는 바로 우리가 3차원 공간에서 살고 있으며, 4차원 공간을 직접 본 적이 없기 때문이다. 또한 일상 생활에서 4차원을 그려야 할 일도 없어 4차원 공간의 모습이 쉽게 떠오르는 것이 오히려 신기한 일이다. 따라서 4차원 도형을 구현한 영상을 보아도 3차원 물체가 연결된 채로 원운동과 자유변형까지 하는것을 알아보는것은 매우 힘든일이다.[5]
4차원 입체도형
4차원에서 재현되는 도형을 보다 쉽게 이해하기 위해선 0차원에서 시작해 4차원까지 직관적으로 차원을 확장해나가야 한다. 먼저 수학에서의 0차원은 점이다. 0차원은 독립적으로 움직일 수 있는 성분이 존재하지 않기 때문에, 어떤 방향으로도 움직일 수 없고 단지 위치값만을 가진다. 점을 한 방향으로 늘리면 1차원 도형인 선분이 된다. 이렇게 생성된 선분을 다시 수직방향으로 아까와 동일한 길이만큼 늘리면 2차원 도형인 정사각형이, 정사각형을 다시 일정한 길이만큼 수직으로 늘리면 3차원 도형인 정육면체가 만들어진다. 따라서 4차원 도형도 3차원인 정육면체를 수직으로 늘리면 얻을 수 있다. 이렇게 얻는 4차원 입체도형을 초입방체라고 부른다.[7]
종류
- 정다포체 - 다포체란 n차원 유클리드 초공간에서 다각형이나 다면체 등의 도형을 임의의 차원으로 확장한 것을 가리키며, 정다포체는 구성하고있는 다포체가 서로 합동인 (n-1)차원의 포로 이루어져 있는것을 말한다. 이러한 도형들을 2차원에서는 정다각형, 3차원에서는 정다면체, 4차원 이상에서는 정다포체라고 부른다.[5] 4차원에서의 정다포체는 오직 6개만이 존재할 수 있다.[8]
- 정오포체, 정팔포체, 정십육포체, 정이십사포체, 정백이십포체, 정육백포체
- 초기둥
- 4차원 초각기둥(Hyperprism) - 두 개의 4차원 방향으로 평행한 3차원 다면체 사이에 선을 그어 형성되는 도형이다. 4차원 초각기둥은 총 두 개의 다면체와 그 다면체를 이루는 면의 개수만큼의 각기둥으로 구성된다.
- 구 초기둥(Spherinder / Spherical cylinder) : 밑포가 구로 이뤄진 초기둥이다. 초각기둥과 같이 평행한 두 개의 구 사이에 4차원 공간을 채우는 4차원 도형으로 이루어진다.
- 원뿔 초기둥(Coninder / Conical cylinder) : 밑포가 원뿔으로 이뤄진 초기둥이다. 다른 초기둥들과 같이 이루어져 있고, 밑포의 종류에 따라 이름이 다르게 붙여진다.
- 원기둥 초기둥(Cubinder / Cubical Cylinder) : 밑포가 원기둥으로 이뤄진 초기둥이다. 다른 초기둥들과 같이 이루어져 있고, 밑포의 종류에 따라 이름이 다르게 붙여진다.
- 초뿔
- 4차원 초각뿔: 하나의 다면체를 4차원 공간상의 꼭짓점과 이어서 만든 도형이다.
- 구 초뿔(Sperone) : 밑포가 구로 이뤄진 초뿔이다.
- 다이콘(Dicone): 원뿔의 모든 지점을 4차원 공간상의 한 꼭짓점과 이어서 만든 도형이다. 두 개의 원뿔이 붙은 것과 비슷한 모양이라고하여 다이콘이라고 부르기도 한다.
- 원기둥 초뿔(Cylindrone / Cylinderical Cone) : 밑포가 원기둥으로 이뤄진 초뿔이다.
- 정육면체 뿔(Cubic Pyramid) : 밑포가 정육면체로 이뤄진 초뿔이다. 정팔포체의 각 포에 정육면체 뿔을 붙이면 정이십사포체를 만들 수 있다.[5]
- 토러스 - 구를 4차원 축에서 회전한 모양과 같다. 회전한 구가 시작한 구와 접하면 체 하나가 사라진다.[9]
- 토러스 초기둥(Torinder) : 밑포가 토러스로 이뤄진 초기둥이다.
- 구 토러스(Spheritorus): 구를 특정 축으로 회전시켜 얻을 수 있는 도형이다. 토러스 구와 위상수학적으로 한 쌍을 이루는 쌍대 관계이다.
- 토러스 구(Torisphere) : 구 초기둥을의 양쪽 끝을 휘어 자신의 안쪽으로 연결해 얻는 도형이다. 토러스와 위상수학적으로 한 쌍을 이루는 쌍대 관계이다.
- 다이토러스(Ditorus) : 토러스 초기둥의 양쪽 끝을 휘어 자신의 안쪽으로 연결하면 얻을 수 있는 도형이다.
- 타이거(Tiger) : 토러스의 각 단면이 되는 원을 다시 다른 방향으로 토러스의 형태로 회전시켜 얻어지는 도형으로, 일반인들이 이해하기 가장 난해한 형태의 도형이다.
- 크로스캡 : 토러스 한쪽 부분의 안팎을 뒤집은 모양의 도형이다. 클라인의 병과 같아 보이지만 다른 도형이다.
- 듀오프리즘(Duoprism) : 한 가지 또는 두 가지의 각기둥을 4차원 방향으로 서로 둘러싸도록 접어 얻을 수 있는 4차원 도형이다. 두 각기둥의 밑면의 개수와 꼭짓점 개수에 따라 (p-q 듀오프리즘)으로 표기한다. p,q의 순서는 무관하다.
예를 들면 삼각기둥 5개와 오각기둥 3개를 서로 둘러싸게 접어 만든 듀오프리즘은 3-5 듀오프리즘 또는 5-3 듀오프리즘이다. 이중에서도 4-4 듀오프리즘은 '테서랙트'라고 부른다.
- 프리즈믹 실린더(Prismic Cylinder) : 원기둥 하나와 각기둥 하나를 4차원 방향으로 서로 둘러싸이도록 접어 만들 수 있는 도형이다. 듀오프리즘과 듀오실린더의 중간 형태로 이다.
- 듀오실린더 : 듀오프리즘의 원기둥 버전이다. 두 개의 원기둥을 서로 둘러싸도록 토러스형으로 접어 만들 수 있는 4차원 도형이다. 총 두 개의 토러스형 초입체로 구성되어 있고 면은 한 개이며, 모서리와 꼭짓점은 존재하지 않는다.
- 초구: n차원 곡면으로, (n+1)차원 공간의 특정한 지점에서 같은 거리에 존재하는 점들의 집합이다. 어느 방향으로 잘라도 항상 단면이 구로 나온다.
- 알렉산더의 뿔 달린 구 : 초구와 위상동형인 도형이다. 구 일부를 뿔처럼 늘린 뒤 꼬아놓은 모양과 같다.
- 클라인의 병: 3차원 곡면으로, 뫼비우스의 띠의 4차원 버전이다. 안과 밖이라고 부르는 부분이 따로 존재하지 않는다.
- 사영평면 : 원의 마주보는 점을 빈틈없이 접어 얻을 수 있는 도형이다.
- 쌍각뿔 : 초기둥과 한 쌍을 이루는 쌍대다포체이다.
- 엇각기둥 : 윗입체와 아랫입체가 한 쌍을 이루는 쌍대다포체 관계이다. 옆입체에는 n각뿔 모양과 삼각뿔 모양, 총 2가지 종류가 있다. 윗입체 혹은 아랫입체와 면을 맞닿는 입체는 n각뿔 모양을 하고, 윗입체, 아랫입체와 동시에 모서리만 접하는 입체는 삼각뿔 모양으로 이뤄진다.
- 엇쌍각뿔 : 엇각기둥과 한 쌍을 이루는 쌍대다포체이다.
- 균일 4차원 다포체 : 아르키메데스 다면체의 4차원 버전이다.
- 쌍곡포물입체, 타구포물입체, 타구입체 등[5]
4차원 도형 재현
3차원을 2차원에 완벽히 표현할 수 없으나 3차원의 그림자를 2차원에 투영할 수 있는 것과 같이, 시각적으로 재현한 4차원 도형들은 사실 3차원에 투영된 실제 4차원 도형의 그림자를 구현한 이다. 3차원 공간에 살고 있는 우리는 4차원 도형을 상상하기 힘들며 표현하기는 불가능하기 때문이다. 우리가 알고 있는 4차원 도형들은 실제 모습이 아닌, 모두 3차원 공간의 인간의 상상으로 만들어낸 가상의 도형들이다.[5] 3차원의 정육면체의 각 면은 정사각형으로 이루어져 있으나 2차원의 평면에 그려내면서 실제모습과는 다르게 앞면과 뒷면을 제외하고는 평행사변형으로 표현되는 등 왜곡이 일어난다. 2차원 평면에 3차원을 그리려면 한차원만 확장하면 되기 때문에 약간의 왜곡만이 일어나지만 4차원을 2차원에 그려내는 일은 두개의 차원을 확장하는 것 이기 때문에 더욱 심한 왜곡과 한계가 생긴다.[7]
4차원의 도형을 보다 정확하게 재현하는 방법은 바로 전개도를 이용하는 것이다. 정육면체를 전개해서 2차원 면으로 구성된 전개도를 만들고 다시 1차원인 선끼리 붙여 정육면체를 만드는 방법과 같이 4차원 초입방체에서 접힌 부분을 펴내면 모든 각이 직각을 이룬 8개의 정육면체가 맞붙은 십자가 모양의 전개도가 나온다. 이 전개도를 다시 2차원면끼리 맞붙이면 4차원 초입방체가 된다.[7]
테서랙트
테서렉트는 영국 출신의 수학자 찰스 하워드 힌턴(Charles Howard Hinton)이 1888년 4차원물체의 시각화를 돕기 위해 고안한 개념으로, 듀오 프리즘의 한 종류이며 4차원 초입방체 또는 정팔포체 라고도 한다. 3차원 도형인 정육각형의 전개도를 만들면 2차원의 정사각형으로 구성되어있는것 처럼, 4차원인 테서랙트를 전개도로 만들면 3차원인 정육각형으로 구성되었다. 인간의 감각기관은 4차원 이상을 인지 할 수 없기 때문에 테서랙트를 3차원 공간에 투영된 형태로 인지한다.[10] 따라서 관련 테서랙트의 모습을 보면 실제 모양을 보면 상상하기 힘들지만, 4차원 공간상에서의 테서랙트는 모든 정육면체가 서로 수직이고 각 정육면체의 평면도 직각을 이룬다. 위 자료의 테서랙트는 4차원 공간 축을 따라 회전하는 테서랙트이다. 3차원 물체 2개가 연결된 채 원운동과 자유변형까지 동시에 하기 때문에 알아보기 힘들지만, 사실 테서랙트의 회전 중에서는 비교적 단순한 형태의 움직임을 구현한것 이다.[7] 한편 테서랙트를 여러 개 활용하면 더 고차원의 도형을 만들 수 있다. 테서랙트10개를 한 모서리당 3개씩 만나도록 연결하면 5차원 도형인 펜터랙트(Penteract)가 만들어진다.[10] 테서랙트가 미지의 영역에 대한 신비로움을 담은 4차원의 상징이 되면서, 테서랙트라는 개념이 발표 된 후 과학뿐만 아니라 여러 인문철학, 예술 등에도 많은 영향을 미쳤다.
- 스페인의 초현실주의 화가인 살바도르 달리(Salvador Dalí)는 이 초입방체의 전개도를 자신의 작품에 그려넣기도 했다.
물리학 관점
예술
영화
인터스텔라
영화관
씨지브이(CGV)
롯데시네마
엠엑스포디(MX4D)
그림
https://terms.naver.com/entry.naver?docId=3568440&cid=58944&categoryId=58970 https://blog.naver.com/ian3714/220293166087 스페인의 초현실주의 화가인 살바도르 달리(Salvador Dalí)는 이 초입방체의 전개도를 자신의 작품에 그려넣기도 했다
각주
- ↑ 〈4차원 (r20210301판)〉, 《더위키》
- ↑ 2.0 2.1 〈공간〉,《위키백과》
- ↑ 〈유클리드 공간〉, 《위키백과》
- ↑ 〈4차원〉, 《위키백과》
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 〈4차원〉, 《나무위키》
- ↑ 이광연, 〈4차원 세계의 모습〉, 《네이버 지식백과》, 2009-01-13
- ↑ 7.0 7.1 7.2 7.3 〈4차원 입체도형〉, 《네이버 지식백과》
- ↑ 〈4차원 정다포체〉, 《위키백과》
- ↑ Lee Sunggil, 〈수학story (7) 4차원 토러스(torus)〉, 《광고. 그이상의 가치》, 2016-07-30
- ↑ 10.0 10.1 〈테서랙트〉, 《나무위키》
참고자료
- 〈4차원 (r20210301판)〉, 《더위키》
- 〈공간〉,《위키백과》
- 〈유클리드 공간〉, 《위키백과》
- 〈4차원〉, 《나무위키》
- 〈4차원〉, 《위키백과》
- 이광연, 〈4차원 세계의 모습〉, 《네이버 지식백과》, 2009-01-13
- 〈4차원 정다포체〉, 《위키백과》
- Lee Sunggil, 〈수학story (7) 4차원 토러스(torus)〉, 《광고. 그이상의 가치》, 2016-07-30
- 〈테서랙트〉, 《나무위키》
같이 보기
